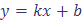Лекция 1. Линии на плоскости

 

Оглавление

 

§1. Системы координат

Аналитическая геометрия

Числовая ось

Прямоугольная система координат на плоскости

Прямоугольная система координат в пространстве

§2. Прямая на плоскости

Уравнение линии (кривой) на плоскости

Уравнение прямой с угловым коэффициентом

Уравнение прямой, проходящей через две точки

Уравнение прямой, проходящей через данную точку в заданном направлении

Уравнение прямой в отрезках

Общее уравнение прямой

§3. Параллельность и перпендикулярность прямых на плоскости

Параллельность

Перпендикулярность

§4. Простейшие задачи

Длина отрезка

Деление отрезка в данном отношении

Расстояние от точки до прямой

 

 

§ 1. Системы координат

 

Аналитическая геометрия – раздел математики, изучающий геометрические объекты алгебраическими методами.

Что подразумевается под геометрическими объектами?

Это, конечно, точки, прямые и плоскости, которые, вообще говоря, в геометрии являются неопределяемыми понятиями. Кроме того, это любая линия или фигура на плоскости и в пространстве: треугольник, окружность, куб, спираль и т.д.

Любой геометрический объект можно представить как совокупность точек, удовлетворяющих некоторым условиям, т.е. как некоторое геометрическое место точек. Например, окружность – это геометрическое место точек, равноудаленных от данной точки (центра окружности).

Для применения алгебраических методов к исследованию геометрических объектов, необходимо найти способ, как описать геометрические точки с помощью алгебраических конструкций. Для этого вводят систему координат.

Числовой осью называется прямая, служащая для изображения действительных чисел, на которой выбрана начальная точка О, единица измерения и направление.

Точка М на этой прямой характеризуется определенным числом (х), координатой, которое по модулю равно длине отрезка ОМ, а знак этого числа зависит от расположения точки М относительно точки О.

 

Рис.1

 

Две взаимно перпендикулярные числовые оси Ох и Оу, имеющие общее начало и одинаковую единицу измерения, образуют прямоугольную (декартову)^[9] систему координат на плоскости ^[10] .

Ось Ох называется осью абсцисс, ось Оу – осью ординат, точка О – началом координат, а плоскость Оху – координатной плоскостью.

Каждой точке координатной плоскости соответствует пара чисел (х; у), называемых ее координатами. Эти числа равны координатам проекций точки М на соответствующие числовые оси.

 

Рис.2

Три взаимно перпендикулярные числовые оси Ох, Оу и Оz, имеющие общее начало и одинаковую единицу измерения, образуют прямоугольную систему координат ^[11] в пространстве ^[12].

Ось Оz называется осью аппликат.

Каждой точке пространства соответствует тройка чисел (х; у; z), называемых ее координатами. Эти числа равны координатам проекций точки М на соответствующие числовые оси.

 

Рис.3

Таким образом, введя систему координат на прямой, на плоскости или в пространстве, мы устанавливаем взаимно однозначное соответствие:

- между действительными числами и точками числовой прямой,

- между упорядоченными парами чисел и точками координатной плоскости,

- между упорядоченными тройками чисел и точками в пространстве.

Это значит, что вместо реальных точек на прямой, на плоскости или в пространстве мы можем оперировать соответствующими числами, парами чисел или тройками чисел, т.е. мы можем перейти от геометрии к алгебре!

 

§ 2. Уравнение линии на плоскости

 

Уравнение линии является важнейшим понятием аналитической геометрии.

Пусть на плоскости имеется некоторая линия (кривая). Координаты х и у точки, лежащей на этой линии, не могут быть произвольными, они должны быть определенным образом связаны. Такая связь аналитически записывается в виде некоторого уравнения.

Уравнением линии (кривой) на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

В общем случае уравнение линии может быть записано в виде или (если это возможно) , где и – некоторые функции.

Рассмотрим нахождение уравнения некоторой линии на примере.

Пример. Найти уравнение множества точек равноудаленных от точек и В (–2; –6).

Решение.

Пусть точка М (х; у) – произвольная точка искомой линии, тогда согласно условию АМ = ВМ. Запишем формулы длины отрезков:

;

.

Т.к. по условию АМ = ВМ, то

С точки зрения геометрии, геометрическое место точек, равноудаленных от концов отрезка, – это его серединный перпендикуляр. Полученное нами уравнение – это его уравнение.

 

Любую линию в принципе можно выразить соответствующим уравнением (хотя на практике это не всегда просто сделать). Однако не всякое уравнение определяет на плоскости линию. Например, уравнение определяет только одну точку О (0; 0), а уравнение не определяет никакого множества точек, ибо левая часть уравнения не может равняться нулю.

 

§ 3. Уравнение прямой на плоскости

 

В геометрии прямую можно задать разными способами, поэтому в аналитической геометрии встречаются различные уравнения прямой.

1. Уравнение прямой с угловым коэффициентом.

Пусть прямая пересекает ось Оу в точке В (0; b) и образует с осью Ох угол α.

Возьмем на прямой произвольную точку М (х; у).

Рассмотрим прямоугольный треугольник МАВ, в котором катет МА = у – b, катет ВА = х. Тогда тангенс угла МВА (угла α) равен .

Введем угловой коэффициент прямой , получим

 

Надо заметить, что уравнение такого вида не может задать «вертикальную» прямую, т.к. при этом угол α = 90° и не существует.