
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Понятие векторного пространстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§1. Элементы теории множеств Бинарные операции Группа Кольцо Поле §2. Определение векторного пространства
§ 1. Элементы теории множеств.
Центральными понятиями линейной алгебры являются вектор и векторное пространство. В курсе математики средней школы дается понятие вектора, как направленного отрезка. Однако в линейной алгебре векторы изучаются с самой общей точки зрения, и вектором называется элемент любого векторного пространства, т.е. множества, обладающего определенными свойствами. При таком подходе вектор как направленный отрезок – лишь частный случай, (пример, модель) этого понятия. Итак, попробуем определить понятие вектор и векторное пространство аксиоматически. Для этого изучим некоторые элементы теории множеств.
Бинарные операции. В самом начале изучения высшей математики, мы говорили, что математика – это наука, изучающая множества и действия с ними. При этом не важно, из чего состоят эти множества, важно только, какими свойствами они обладают. В зависимости от набора свойств множества выделяют в различные классы. Например, ограниченные множества, конечные множества и т.д. Между элементами множеств можно установить соответствие по некоторому правилу. При этом в случае числовых множеств, мы говорим, что задана функция, если же рассматривать множества вообще, то говорят, что задана операция (отображение, оператор). Рассмотрим примеры различных операций между множествами: 1. Рассмотрим множество А – множество слов русского языка и множество натуральных чисел N. Зададим операцию «длина слова» из множества А в множество N («длина слова»: 2. Рассмотрим множество М – множество квадратных матриц и множество действительных чисел R. Зададим операцию «определитель» из множества М в множество R («определитель»: 3. Рассмотрим множество С – множество студентов нашего института и множество Р – множество всех населенных пунктов. Зададим операцию «родина» из множества С в множество Р («родина»:
Элемент, для которого ищется соответствие (т.е. к которому применяется операция) называется операндом, а найденный в операции элемент – результатом. Мы рассмотрели примеры операций с одним операндом. Если операция двум элементам (операндам) ставит в соответствие один результат, она называется бинарной операцией. Например: 1. Снова рассмотрим множество А – множество слов русского языка. Зададим операцию «склеивание» по правилу: любым двум словам поставим в соответствие слово, составленное подряд из букв первого и второго слов, например, «Вася» и «студент» ® «Васястудент». Это бинарная операция. Здесь операнды берутся из множества А, а вот результат лежит в другом множестве – множестве упорядоченных наборов букв русского языка. Обозначим это множество буквой В, тогда можно записать, что бинарная операция «склеивание» задана из множества А в множество В: «склеивание»: 2. Сложение чисел, известное нам из школы, – это тоже бинарная операция, она любым двум числам ставит в соответствие другое число, найденное по правилам сложения. Если рассматривать сложение на множестве действительных чисел R, то можно записать, что бинарная операция «сложение» задана из множества R в множество R: «+»: Если и операнды, и результат операции лежат в одном множестве, как в случае сложения чисел, говорят, что операция задана на этом множестве. При этом можно использовать сокращенную запись (R, +)
Бинарную операцию принято обозначать знаком действия, который ставится между операндами. Например, для операции сложения используется знак +, а результат её применения к двум элементам x и y записывается в виде x + y. Существуют унарные, тернарные и другие операции с различной «арностью», т.е. с разным количеством операндов, но мы будем рассматривать только бинарные операции.
Группы, кольца, поля. Бинарные операции могут обладать различными свойствами (коммутативность, ассоциативность, дистрибутивность и др.). В зависимости от набора этих свойств, множество, на котором задана одна или несколько бинарных операций называется группой, кольцом или полем[8].
Непустое множество G с заданной на нём бинарной операцией * (G, *) называется группой, если выполнены следующие условия:
1) операция * ассоциативна: 2) в множестве G есть нейтральный элемент:
3) у любого элемента из множества G есть обратный элемент:
Если дополнительно выполняется условие коммутативности:
множество G называется коммутативной группой.
Пример 1. Множество целых чисел – коммутативная группа по сложению: 1) для любых целых чисел 2) среди целых чисел есть нейтральный элемент по сложению – число 0, такой, что для любого целого числа 3) для любого целого числа есть обратный элемент по сложению, он называется противоположный 4) для целых чисел выполняется условие коммутативности:
Пример 2. Множество целых чисел – не образует группу по умножению: 1) для любых целых чисел 2) среди целых чисел есть нейтральный элемент по умножению – число 1, такой, что для любого целого числа 3) но обратные элементы по умножению для целых чисел не являются целыми – это дроби. Например, для 2 обратный элемент по умножению – это А вот если рассмотреть множество рациональных чисел, то 3-е условие группы будет выполнено. Кроме того, выполняется и условие коммутативности умножения:
Рассмотрим множество К, на котором заданы две бинарные операции: сложение (+) и умножение (·). Множество К называется кольцом, если: 1) оно является коммутативной группой по сложению; 2) умножение ассоциативно: 3) операция умножения дистрибутивна относительно сложения как слева, так и справа:
Если, кроме того, умножение коммутативно, т.е.
Если на множестве задаются две бинарные операции, то нейтральный элемент операции «сложение» обычно называют «нулем», а нейтральный элемент операции «умножение» называют «единицей». Если кольцо содержит нейтральный элемент по умножению (единицу), его называют кольцом с единицей.
Пример. 1. Множество целых чисел с операциями сложение и умножение – коммутативное кольцо с единицей. 2. Множество четных чисел с операциями сложение и умножение – коммутативное кольцо без единицы.
Коммутативное кольцо с единицей отличной от нуля (1 ¹ 0) называется полем, если все его ненулевые элементы обратимы. Иными словами, множество Р с двумя бинарными операциями: сложение (+) и умножение (·); называется полем, если: 1) оно образует коммутативную группу по сложению; 2) все его ненулевые элементы образуют коммутативную группу по умножению; 3) умножение дистрибутивно относительно сложения как слева, так и справа.
Пример: множество рациональных чисел Q и множество действительных чисел R с операциями сложение и умножение чисел, т.е. (Q, +, ·) и (R, +, ·), – поля.
Основываясь на аксиомах группы, кольца или поля, можно вывести свойства этих типов множеств, которые одинаковы для любого множества такой же структуры.
Пример. Рассмотрим множество упорядоченных пар действительных чисел
Зададим на этом множестве операцию сложения так:
При этом нулем будет нулевая пара чисел (0, 0), обратным элементом относительно сложения для пары чисел Зададим операцию умножения так:
В этом случае, множество R 2 является полем.
§ 2. Определение векторного пространства
Вернемся к понятию векторного пространства. Пусть V – некоторое непустое множество, элементы которого будем обозначать Пусть заданы и определены каким-либо образом две бинарные операции: 1. Аддитивная операция (или операция сложения) «Å», когда любым двум элементам множества V ставится в соответствие элемент того же множества (Å: V ´ V ® V). 2. Умножение на скаляр «∘», когда любому элементу поля Р и любому элементу множества V ставится в соответствие элемент множества V (∘: P ´ V ® V). Множество V называется векторным пространством над полем Р если выполняются условия: 1. Относительно операции сложения «Å» множество V образует коммутативную группу; 2. Для любых двух элементов множества V 1) 2) 3) 4)
Элементы векторного пространства называются векторами.
Рассмотрим примеры векторных пространств. 1). Множество квадратных матриц п-го порядка Рассмотрим множество квадратных числовых матриц п -го порядка с операциями сложение матриц и умножение матрицы на число, определенными нами ранее. Это – векторное пространство над полем действительных чисел. Докажем это. 1. Надо доказать, что множество квадратных матриц – группа по сложению. 1) ассоциативность: А + (В + С) = (А + В) + С – рассматривалось ранее; 2) коммутативность: А + В = В + А – рассматривалось ранее; 3) нейтральным элементом является нулевая квадратная матрица п -го порядка 0, т.к. при сложении с нулем как слева, так и справа элементы матрицы не изменятся; 4) обратным элементом для любой матрицы будет матрица, составленная из противоположных чисел соответственно. Например, для матрицы Итак получили, что множество квадратных матриц – группа по сложению.
2. Теперь проверим выполнение 4-х равенств. Ранее мы рассматривали свойства операции умножения матрицы на число и говорили, что выполняются следующие свойства: 1) 2) 3) Нетрудно убедиться, что выполняется и четвертое равенство, т.к. умножение матрицы на единицу не изменяет саму матрицу: 4) Таким образом, выполнены все условия, следовательно, множество квадратных числовых матриц п -го порядка с операциями сложение матриц и умножение матрицы на число – векторное пространство над полем действительных чисел.
2). Любое поле является векторным пространством над самим собой. Это можно проверить на множестве действительных чисел.
3). Арифметическое пространство. Рассмотрим множество упорядоченных пар действительных чисел 1. Введем на этом множестве аддитивную операцию Å по такой формуле:
2. Определим операцию умножения на скаляр из поля действительных чисел (R, +, ·) следующим образом:
Множество Действительно, ранее мы доказали, что множество упорядоченных пар чисел – это поле, следовательно, оно является коммутативной группой по сложению. Что же касается выполнения 4-х равенств, их легко доказать, опираясь на свойства действительных чисел: 1) и
2) и
3)
4)
4). Множество геометрических векторов. Множество геометрических векторов с бинарными операциями сложение векторов и умножение вектора на число образует векторное пространство над полем действительных чисел. Доказательство рассмотрим на следующем занятии.
Подводя итог сегодняшнему занятию, заметим, что понятие векторного пространства определяется не природой образующих его элементов, а правилами действий над этими элементами, в качестве которых могут выступать реальные векторы, матрицы, функции или иные математические объекты.
Векторы
|
||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.71.40 (0.012 с.) |

 ) по правилу: каждому слову поставим в соответствие натуральное число, равное количеству букв в этом слове.
) по правилу: каждому слову поставим в соответствие натуральное число, равное количеству букв в этом слове. ) по правилам, определенным ранее.
) по правилам, определенным ранее. ) по правилу: каждому студенту поставим в соответствие населенный пункт, в котором он родился.
) по правилу: каждому студенту поставим в соответствие населенный пункт, в котором он родился.
 .
. ;
;

 ,
, ;
; ;
; такой, что
такой, что  ;
; .
. ;
; ;
; :
:  .
. , следовательно, множество рациональных чисел – коммутативная группа по умножению.
, следовательно, множество рациональных чисел – коммутативная группа по умножению. ;
;
 , множество К называется коммутативным кольцом.
, множество К называется коммутативным кольцом.
 .
. является пара противоположных чисел
является пара противоположных чисел  .
. . При этом единицей будет – пара чисел (1, 0), обратным элементом относительно умножения для пары чисел
. При этом единицей будет – пара чисел (1, 0), обратным элементом относительно умножения для пары чисел  .
. ,... и (Р, +, ·) – некоторое поле.
,... и (Р, +, ·) – некоторое поле.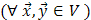 и любых двух элементов поля Р
и любых двух элементов поля Р  справедливы равенства:
справедливы равенства: ;
; ;
; ;
; .
.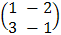 обратным (противоположным) элементом будет матрица
обратным (противоположным) элементом будет матрица  , при сложении они дадут нейтральный элемент, т.е. нулевую матрицу.
, при сложении они дадут нейтральный элемент, т.е. нулевую матрицу. ;
; ;
; .
. .
. .
. .
.
 с описанными бинарными операциями является векторным пространством над полем действительных чисел.
с описанными бинарными операциями является векторным пространством над полем действительных чисел.

 ;
;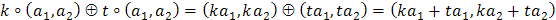 ;
;



 .
.


