Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение n- мерного векторного пространства. Свойства.Содержание книги
Поиск на нашем сайте
Векторное пространство называют. n-мерным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e 1, e 2,... e n, а любые n+1 элементов линейно зависимы. Векторное пространство называют бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мерного векторного пространства образуют базис этого пространства. Если e 1, e 2,... e n - базис векторного пространства, то любой вектор x этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов: Примеры векторных пространств: Множество всех векторов 3-мерного пространства образует векторное пространство. Более сложным примером может служить так называемое n-мерное векторное пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел (λ1, λ2,..., λn). Сумма двух векторов и произведение на число определяются соотношениями: Множество L всех многочленов α0 + α1 u +... + αn u n (любых степеней n) от одного переменного с действительными коэффициентами α0, α1,..., αn с обычными алгебраическими правилами сложения многочленов и умножения многочленов на действительные числа образует векторное пространство. Многочлены 1, u, u 2,..., u n (при любом n) линейно независимы в L, поэтому L - бесконечномерное векторное пространство. Многочлены степени не выше n образуют векторное пространство размерности n+1; его базисом могут служить многочлены 1, u, u 2,..., u n. Скалярное произведение векторов. Пример в д. метеорологии. Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора а на проекцию другого вектора b на данный вектор а.
Из ф-лы следует, что Для любых векторов a, b и c и любого числа λ справедливы равенства: 1. 2. 3. 4. Если векторы
то их скалярное произведение может быть вычислено по формуле
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
Угол
дается формулой Векторное произведение векторов. Пример в динам. Метеорологии Если для определение физ величины. Кроме численного значения, необходимо указать направление в пространстве, то такие величины называют векторами. Векторным произведением АхВ двух векторов называется вектор С = А*В (рис.), направленный перпендикулярно плоскости векторов-сомножителей в ту сторону, откуда поворот от первого сомножителя ко второму на меньший угол против хода часовой стрелки и равный по величине площади параллелограмма, построенного на этих векторах, т.е. |C|=|A*B|=ABsin(A,B)
Векторное произведение векторов определяется следующими условиями: 1). Модуль вектора |С| равен ABsin(A,B), где (A,B) - угол между векторами A и B; 2). Вектор |C| перпендикулярен к каждому из векторов A и B; 3). Направление вектора |С| соответствует «правилу правой руки». Это означает, что если векторы A, B и |С| приведены к общему началу, то вектор |С| должен быть направлен так, как направлен средний палец правой руки, большой палец которой направлен по первому сомножителю (то есть по вектору A), а указательный - по второму (то есть по вектору B). Векторное произведение зависит от порядка сомножителей, именно: Необходимое и достаточное условие параллельности векторов имеет вид: А*В=0. Если система координатных осей правая и векторы А и В заданы в этой системе своими координатами:
то векторное произведение вектора А на вектор В определяется формулой
Пример в динамич метеорологии: Такие векторы, направление которых устанавливается соглашением и которые изменяют свое направление при замене правой системы координат на левую, называются аксиальными, например момент силы и угловая скорость. Векторы, направление которых определяется физическим смыслом и которые не меняют своего направления при изменении системы координат, называют полярными, например сила и скорость.
24. Понятие тензора. Пример в динам. Метеорологии Те́нзор (от лат. tensus, «напряженный») — объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры, векторы, билинейные формы и т.п. Скаляр или тензор нулевого ранга — физическая величина, полностью определяемая в любой координатной системе одним числом (или функцией), которое не меняется при изменении пространственной системы координат. Скаляр имеет одну компоненту. Таким образом, если ф — значение скаляра в одной системе координат, а ф' — в другой, то ф'=ф. Векторы — величины более высокого ранга по сравнению со скалярами; они могут быть названы тензорами 1-го ранга. Три числа или функции, определяющие вектор, меняются при изменении пространственной системы координат, но по такому закону, что в любой из координатных систем они определяют один и тот же вектор. Если в пространстве задан вектор А, то его компоненты А1 определятся, если выбрана какая-то система (К) декартовых координат. В другой системе координат (К") его компоненты, естественно, будут другими А'i, хотя сам вектор А остается неизменным, в том смысле, что А'i определяют тот же самый вектор. Для того чтобы обеспечивалась неизменность вектора в этом смысле, независимость его как физической величины от выбора системы координат, необходимо, чтобы его компоненты менялись так же, как и координаты точки: Некоторые геометрические объекты, а также целый ряд физических свойств, требуют для своей характеристики больше чем трех чисел (или функций). Это приводит к понятию величин, тензорные свойства которых сложнее, чем у векторов и скаляров. Эти величины, тензоры 2-го ранга, не могут быть составлены в виде простого набора векторов или скаляров. Это — качественно новые величины, отвечающие физическому или геометрическому смыслу описываемых объектов. Тензор 2-го ранга — физическая величина, определяемая в любой системе координат девятью числами (или функциями) Aik, которые при изменении системы координат преобразуются в A'ik по закону Величины Тензор n-го ранга — физическая величина, определяемая в каждой системе декартовых координат совокупностью 3nчисел или функций Аkl... (n —число индексов), которые при изменении системы координат преобразуются по закону
Сумма справа является однородной функцией (формой) степени n относительно косинусов углов 27. Ковариантное и контравариантное преобразование Ковариантность и контравариантность — математическое и физическое понятие, которое описывает то, как величины изменяются при преобразовании системы координат.
Общее определение ковариантности и контравариантности исходит из того, как компоненты объектов преобразуются при изменении базиса. Пусть V — векторное пространство размерности n над полем скаляров S, и пусть каждый из f = (X 1,…, Xn) и f' = (Y 1,…, Yn) — базис V. Также, пусть изменение базиса из f в f′ даётся
для некоторой обратимой n × n матрицы A с величинами
Контравариантные преобразования Вектор v в V представляется единственным образом как линейная комбинация элементов f базиса как
где vi [f] — это скаляры из S известные как компоненты v в f базисе. Обозначают вектор столбец компонентов v как v[f]:
поэтому (2) может быть переписано как произведение матриц
Вектор v может также быть выражен в виде f' базиса, поэтому
Однако, так как вектор v сам инвариантен при изменении базиса,
Инвариантность v комбинирует с отношением (1) между f и f' обеспечивает
что дает правило преобразования
В виде компонент,
,где коэффициенты Ковариантные преобразования Линейный функционал α на V представляется единственным образом в виде sкомпонент (скаляров в S) в f базисе как
Эти компоненты есть действие α на базисные вектора Xi f базиса. При изменении базиса из f в f' (1), компоненты преобразуются как
поэтому может быть переписано как произведение матриц
Поскольку компоненты линейного функционала α преобразуются с матрицей преобразования A, говорят, что эти компоненты преобразуются ковариантно при изменении базиса.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.4.227 (0.01 с.) |

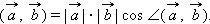

 , если
, если  - острый угол,
- острый угол,  , если
, если  в том и только в том случае, когда векторы
в том и только в том случае, когда векторы  и
и  перпендикулярны (в частности,
перпендикулярны (в частности,  или
или  ).
). причем
причем 
 (переместительный закон).
(переместительный закон). (распределительный закон).
(распределительный закон). (сочетательный закон).
(сочетательный закон). ,
,  ,
,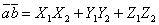 .
. .
. , или в координатах
, или в координатах 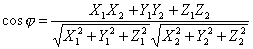 .
.
 .
. ,
, 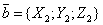 ,
,
 Или С=А*В=(A1i1+A2i2+A3i3)*(B1i1+B2i2+B3i3)=i1(A2B3-A3B2)+i2(A3B1-A1B3)+i3(A1B2-A2B1)
Или С=А*В=(A1i1+A2i2+A3i3)*(B1i1+B2i2+B3i3)=i1(A2B3-A3B2)+i2(A3B1-A1B3)+i3(A1B2-A2B1)


 являются компонентами тензора 2-го ранга. Если компоненты тензора заданы в одной декартовой системе координат (Aik), то по предыдущей формуле можно определить компоненты тензора (
являются компонентами тензора 2-го ранга. Если компоненты тензора заданы в одной декартовой системе координат (Aik), то по предыдущей формуле можно определить компоненты тензора ( . Если все компоненты тензора обращаются в нуль в какой-либо системе координат, то они равны нулю в любой другой системе вследствие однородности закона преобразования.
. Если все компоненты тензора обращаются в нуль в какой-либо системе координат, то они равны нулю в любой другой системе вследствие однородности закона преобразования.
 .
.
 . Здесь, каждый вектор Yj из f' базисов — это линейная комбинация векторов Xi из f базиса, поэтому
. Здесь, каждый вектор Yj из f' базисов — это линейная комбинация векторов Xi из f базиса, поэтому .
. , (2)
, (2)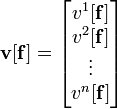
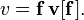
 .
.

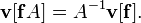

 есть величины обратной матрицы к A. Потому, что компоненты вектора v преобразуются обратно к матрице A, про эти компоненты говорят, что они преобразуются контравариантно при преобразовании базиса.
есть величины обратной матрицы к A. Потому, что компоненты вектора v преобразуются обратно к матрице A, про эти компоненты говорят, что они преобразуются контравариантно при преобразовании базиса.
 . (3)
. (3)