
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Баланс сил в циклоне и антициклоне. Выражения для скорости ветра.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
 Схема градиентного ветра при круговых изобарах имеет большое практическое значение, т.к. она дает простую модель движений воздуха в основных барических образованиях, встречающихся в атмосфере – циклонах и антициклонах. Циклон-барическая обл, ограниченная семейством замкнутых изобар, с минимумом давления в центре; антициклон – барическая обл, но с мах давлением в центре. Свойства градиентного ветра: 1) величина скорости вдоль каждой траектории – круговой изобары – остается постоянной; 2) вертикальные скорости отсутствуют; 3) основным уравнением для градиентного ветра при круговых изобарах явл уравнение: Схема градиентного ветра при круговых изобарах имеет большое практическое значение, т.к. она дает простую модель движений воздуха в основных барических образованиях, встречающихся в атмосфере – циклонах и антициклонах. Циклон-барическая обл, ограниченная семейством замкнутых изобар, с минимумом давления в центре; антициклон – барическая обл, но с мах давлением в центре. Свойства градиентного ветра: 1) величина скорости вдоль каждой траектории – круговой изобары – остается постоянной; 2) вертикальные скорости отсутствуют; 3) основным уравнением для градиентного ветра при круговых изобарах явл уравнение:
Все величины, входящие в уравнение, постоянны вдоль каждой траектории – круговой изобары. Т.к. координата s, вдоль которой отсчитывается скорость V, направлена по движению, то величина V существенно положительна. Радиус кривизны RT положителен, если траектории вдоль движения поворачивают влево, и отрицателен в противоположном случае. Величина wz=w*sin (фи) положительна в северном полушарии и отрицательна в южном. Величина положительна, если давление растет влево от движения, и отрицательна, если убывает. Северное полушарие: траектории вдоль движения поворачивают влево (RT >0) Т.к. оба члена левой части уравнения (1) положительны, то должно быть Вкаждой точке циклона барический градиент направлен по радиусу к центру. Как следует из рис. б, отклоняющая сила FK в антициклоне уравновешивает барический градиент grad p и центробежную силу Fц: FK = grad p +Fц. В центре стационарного антициклона (r=0) ветер обращается в нуль: С удалением от центра скорость градиентного ветра растет (если grad p остается неизменным). В отличие от циклона, где барический градиент, а вместе с ним и скорость градиентного ветра могут принимать любые, в том числе и очень большие значения, барический градиент и скорость градиентного ветра в антициклоне ограничены. В самом деле в антициклоне давление убывает с удалением от центра. 35.Уравнение движения в натуральных координатах. Прямое и обратное преобразование с декартовыми координатами. Наряду с обычными прямолинейными координатами введем криволинейные координаты n и s. Координатные линии направим вдоль скорости ветра в каждый рассматриваемый момент времени, тогда семейство координатных линий s (n=const) будет семейством линий тока. Координатные линии n (s=const) в рассматриваемый момент направим так, чтобы в каждой точке касательная к s=const была перпендикулярна касательной к n=const в той же точке; иначе говоря семейство координатных линий n должно быть ортогонально семейству координатных линий s. Это натуральная система координат (СК).
Преобразовав, получим: Найдем далее выражение для двух важных характеристик движения – горизонтальной дивергенции скорости Горизонтальная дивергенция скорости определяется двумя факторами – изменением модуля скорости вдоль линий тока и сходимостью или расходимостью линий тока. Величину Выведенные выражения для горизонтальной скорости и вертикальной составляющей вихря скорости в натуральных координатах ценны прежде всего тем, что позволяют отчетливо выявить кинематическую природу этих величин.
и приведем их к натуральным координатам.
Умножив (20) на сosβ и (21) на sinβ и сделав необходимые преобразования, получим:
Для получения второго уравнения движения в натуральных координатах умножим (21) на сosβ и (20) на sinβ и из первого результата вычтем второй. Получим:
|
|||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 т.е. влево от движения давление убывает, а значит, соблюден барический закон ветра. В центре – минимум давления. Это – схема циклона в северном полушарии. (рис. а). Траектории вдоль движения поворачивают вправо ((RT <0). Тогда знак левой (а значит, и правой) части уравнения (1) зависит от соотношения абсолютных величин членов, т.е от отношения
т.е. влево от движения давление убывает, а значит, соблюден барический закон ветра. В центре – минимум давления. Это – схема циклона в северном полушарии. (рис. а). Траектории вдоль движения поворачивают вправо ((RT <0). Тогда знак левой (а значит, и правой) части уравнения (1) зависит от соотношения абсолютных величин членов, т.е от отношения  . При условии
. При условии  , когда малые скорости при больших радиусах кривизны изобар, левая часть уравнения (1) положительна, следовательно, т.е. влево от движения давление убывает – соблюден барический закон ветра. В центре – мах давления. Это схема антициклона (рис. б).
, когда малые скорости при больших радиусах кривизны изобар, левая часть уравнения (1) положительна, следовательно, т.е. влево от движения давление убывает – соблюден барический закон ветра. В центре – мах давления. Это схема антициклона (рис. б). Для того, чтобы представить уравнения движения в натуральных координатах, выведем необходимые для такого преобразования формулы. Прежде всего очевидно (рис.43) что:
Для того, чтобы представить уравнения движения в натуральных координатах, выведем необходимые для такого преобразования формулы. Прежде всего очевидно (рис.43) что:


 и вертикальной составляющей вихря скорости
и вертикальной составляющей вихря скорости  С помощью формул (6) и (9) получаем:
С помощью формул (6) и (9) получаем: 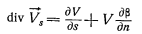 (12) и
(12) и  (13).
(13). называют иногда дивергенцией модуля скорости. Она дает положительное слагаемое, если скорость растет вдоль потока, и отрицательное – если убывает. Вертикальная составляющая вихря скорости определяется двумя факторами – изменением модуля скорости в направлении, поперечном движению, и кривизной линий тока. Величину
называют иногда дивергенцией модуля скорости. Она дает положительное слагаемое, если скорость растет вдоль потока, и отрицательное – если убывает. Вертикальная составляющая вихря скорости определяется двумя факторами – изменением модуля скорости в направлении, поперечном движению, и кривизной линий тока. Величину  наз вихрем модуля скорости, она дает положительное слагаемое, если скорость растет вправо от направления движения, и отрицательное, если скорость растет влево от направления движения.
наз вихрем модуля скорости, она дает положительное слагаемое, если скорость растет вправо от направления движения, и отрицательное, если скорость растет влево от направления движения.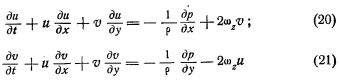 Перейдем к уравнению движения; пренебрегая членами, содержащими вертикальные скорости, запишем эти уравнения в виде:
Перейдем к уравнению движения; пренебрегая членами, содержащими вертикальные скорости, запишем эти уравнения в виде: Это первое из уравнений движения в натуральной СК, а именно уравнение движения в проекции на линию тока. Введя еще полную производную dV/dt (изменение модуля скорости при движении), которая равна
Это первое из уравнений движения в натуральной СК, а именно уравнение движения в проекции на линию тока. Введя еще полную производную dV/dt (изменение модуля скорости при движении), которая равна  можно записать уравнение движения в виде:
можно записать уравнение движения в виде: 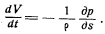
 Это 2-е уравнение движения в натуральной СК, а именно уравнение движения в проекции на направление, ортогональное линиям тока. Вводя с помощью формул
Это 2-е уравнение движения в натуральной СК, а именно уравнение движения в проекции на направление, ортогональное линиям тока. Вводя с помощью формул  радиус кривизны траектории RT, можно переписать уравнение движения в виде:
радиус кривизны траектории RT, можно переписать уравнение движения в виде:  .
.


