
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы, действующие в атмосфере. Массовые и поверхностные силы.Содержание книги
Поиск на нашем сайте
Особенности проявления силы тяжести в атмосфере. Сила тяжести. Одной из массовых сил является сила тяжести действующая на любую как неподвижную, так и на движущуюся относительно Земли частицу воздуха. Сила тяжести g представляет собой векторную сумму двух сил: силы земного притяжения g, направленной к центру Земли, и центробежной силы с, возникающей от вращения Земли вокруг своей оси и направленной по радиусу широтного круга, проходящего через рассматриваемую точку (рис). На рисунке невозможно выдержать правильное соотношение величин этих двух сил, так как центробежная сила слишком мала тяжести по сравнению с силой. Действительно, величина центробежного ускорения определяется: Так как земля вращается вокруг своей оси с постоянной угловой скоростью
Центробежная сила с очень мала по сравнению с силой земного притяжения g, и по мере приближения к полюсу она уменьшается до нуля, а сила тяжести g с увеличением широты увеличивается. Действие силы тяжести определяет форму поверхности мирового океана и в большой мере также форму поверхности суши. Очевидно, что при отсутствии морских течений поверхность моря должна быть всюду перпендикулярна к направлению силы тяжести (иначе касательная составляющая силы тяжести начнет перемещать водные частицы). Такие поверхности называется поверхностями уровня и приближенно представляют собой эллипсоиды вращения, малая ось которых совпадает с осью вращения земли.
Тензор упругих напряжений. Связь с вязкостью. Тензор напряжений — тензор второго ранга, состоящий из девяти величин, представляющих механические напряжения в произвольной точке нагруженного тела. Эти девять величин записываются в виде таблицы, в которой по главной диагонали стоят нормальные напряжения в трёх взаимно перпендикулярных осях, а в остальных позициях — касательные напряжения, действующие на трёх взаимно перпендикулярных плоскостях. Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ. Компоненты тензора напряжений
По индексу
Компоненты
В случае линейной теории упругости тензор напряжений симметричен (так называемый закон парности касательных напряжений).
Ур-ние неразрывности. Уравнение неразрывности, часто называемое также уравнением сплошности, представляет собой частную форму общего закона сохранения массы, установленного Ломоносовым, специализированную для случая сплошной среды. Рассмотрим элементарную массу жидкости δm, заполняющую объём δτ. Если проследить движение частиц жидкости, составляющих данный жидкий объём, то неизменность массы можно выразить соотношением Так как Но Подставляя это выражение в (2) и сокращая на δτ, получаем уравнение неразрывности
Можно перевести уравнение неразрывности также к другой форме, более удобной для дальнейших выводов. Для этого раскроем выражение для индивидуальной производной от плотности и для дивергенции скорости Эта форма уравнения неразрывности наиболее часто используется в метеорологических исследованиях. Для незжимаемой жидкости В спаведливости этого соотношения можно убедиться также непосредственно, вспоминая физический смысл дивергенции скорости. Приведём ещё выражение для уравнения неразрывности в сферической системе координат (для вывода которого достаточно выразить
13 Турбулентность в атмосфере. Изменения в уравнениях Вследствие неравномерности распределения давления в атмосфере ее воздушные массы перемещаются в горизонтальном направлении, вызывая ветер. Скорость ветра и его направление непрерывно изменяются. Средние значения скорости ветра составляют 5-10 м/с, но могут достигать 50 м/с и более. В верхних слоях атмосферы в струйных течениях скорость ветра может превышать 100 м/с. Перемещение воздуха в атмосфере носит турбулентный характер. Сущность явления турбулентности заключается в том, что в массе воздуха, находящейся в движении, образуются вихревые потоки. Эти вихри вызывают хаотические колебания характеристик движущихся масс воздуха, т.е. их скорости, направления, температуры, давления и плотности. Одним из источников возникновения турбулентности является различие скоростей ветра в смежных слоях. Особенно велика турбулентность в нижних слоях тропосферы: в приземном слое высотой 50-100м и в слое трения, простирающемся до высоты 1000-1500м. Турбулентность, вызываемая разностью скоростей в смежных слоях, называется динамической. Кроме горизонтальных перемещений воздушных масс, в атмосфере присутствуют и вертикальные перемещения. Скорости вертикальных перемещений значительно ниже горизонтальных. В обычных условиях вертикальные перемещения измеряются в сантиметрах в секунду. Развитие этих перемещений связано с наличием архимедовой или гидростатической силы. Воздух, более теплый у земной поверхности и, следовательно, менее плотный, чем окружающая среда, перемещается вверх, а более холодный опускается на его место. Вертикальные перемещения воздуха называются конвекцией. При слабом развитии конвекция носит беспорядочный турбулентный характер. При развитой конвекции, над отдельными участками разогретой земной поверхности возникают мощные восходящие и нисходящие токи воздуха, достигающие стратосферы. Нисходящие потоки обычно менее интенсивны, но охватывают на много большие площади. Турбулентное перемешивание в десятки и тысячи раз превышает молекулярное перемешивание или молекулярную диффузию. Турбулентная диффузия приводит к распространению в атмосфере тепла и влаги в вертикальном направлении. Следствием турбулентности является перенос количества движения сверху вниз, что приводит к некоторому выравниванию распределения скорости ветра по высоте. Количество движения определяется выражением , где m – масса воздуха, v – скорость движения этой массы. Поскольку в более высоких слоях атмосферы скорость ветра больше, чем вблизи земной поверхности, то при перемешивании массы воздуха, имеющие более высокие скорости, перемещаются на нижние уровни, в результате чего возникает турбулентное трение. Помимо основных компонентов в состав воздуха входят переменные части: водяной пар, двуокись углерода, озон, а также различные примеси, т.е. мельчайшие твердые и жидкие частицы, называемые, аэрозолями. Количество любой субстанции характеризуется ее удельным содержанием s, т.е. массовой долей субстанции. В процессе турбулентного обмена воздуха любая субстанция распространяется в том направлении, в котором она убывает. Изменение субстанции на единицу расстояния называется ее градиентом. В атмосфере убывание субстанции обычно наблюдается в направлении снизу вверх. Количественной характеристикой турбулентного обмена является поток субстанции, т.е. количество субстанции, переносимой через единицу площади в единицу времени. В соответствии с теорией, переносимая в процессе турбулентного обмена субстанция, должна удовлетворять следующим условиям. 1.Количество субстанции в индивидуальной частице воздуха в процессе ее движения, пока она не смешалась с окружающим воздухом, должно сохраняться неизменным. 2.При смешении двух масс воздуха должно сохраняться общее количество субстанции. 3.Субстанция должна быть пассивной примесью, т.е. не оказывать влияния на турбулентное движение. При соблюдении этих условий поток субстанции пропорционален градиенту массовой доли субстанции. В случае переноса субстанции по вертикали ее поток может быть выражен формулой Sв= -А* dS/dZ, где Sв - вертикальный перенос субстанции, -dS/dZ -вертикальный градиент субстанции, А – коэффициент турбулентного обмена, зависящий от атмосферных условий и характера подстилающей поверхности. Турбулентный перенос тепла в атмосфере носит более сложный характер. Вследствие сжимаемости воздуха и непрерывно происходящих в его толще адиабатических изменений его температуры, о направлении переноса тепла нельзя судить по направлению градиента температуры. При сухоадиабатическом процессе сохраняющейся характеристикой теплового состояния воздушной массы является ее потенциальная температура.
14. Скалярные, векторные, тензорные величины Скалярная величина (от лат. scalaris — ступенчатый) в физике — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только своим значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д. Векторная величина - величина называется вектором (векторной), если она определяется двумя элементами различной природы: алгебраическим элементом - числом, показывающим длину вектора и являющимся скаляром, и геометрическим элементом, указывающим направление вектора. Обозначаются векторные величины соответствующими буквами со стрелкой наверху или выделяются жирным шрифтом. Примеры векторных физических величин: сила; скорость; импульс. Векторы изображают направленными отрезками. Началом вектора называют ту точку, откуда начинается направленный отрезок (точка А на рис. 1), концом вектора – точку, в которой заканчивается стрелка (точка B на рис. 1).
Тензорные величины - объекты линейной алгебры, линейно преобразующие элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры, векторы, билинейные формы и т.п. Термин «тензор» также часто служит сокращением для термина «тензорное поле», изучением которых занимается тензорное исчисление. Многие тензорные величины, ранг тензора которых равен 2 определяются уравнением вида, где и — две векторные физические величины, связанные преобразованием. Примеры: тензор инерции; тензор эффективной массы; тензор диэлектрической проницаемости.
15. Теория подобия. Масштаб. Учение об исследовании физич. явлений, основанное на понятии о физич. подобии. Два физич. явления подобны, если но численным значениям характеристик одного явления можно получить численные значения характеристик другого явления простым пересчетом, к-рый аналогичен переходу от одной системы единиц измерения к другой. Для всякой совокупности подобных явлений все соответствующие безразмерные характеристики (безразмерные комбинации из размерных величин) имеют одинаковое численное значение. Обратное заключение тоже верно, т. е. если все соответствующие безразмерные характеристики для двух явлений одинаковы, то эти явления физически подобны.
Анализ размерностей и П. т. тесно связаны между собой и положены в основу экспериментов с моделями. В таких экспериментах осуществляются замены изучения нек-рого явления в натуре изучением аналогичного явления на модели меньшего или большего масштаба (обычно в специальных лабораторных условиях).
После установления системы параметров, определяющих выделенный класс явлений, устанавливаются условия подобия двух явлений. Именно, пусть явление определяется пнезависимыми параметрами, нек-рые из к-рых могут быть безразмерными. Пусть, далее, размерности определяющих переменных и физич. постоянных выражены через размерности kиз этих параметров с независимыми размерностями (
Определенный соответствующей постановкой задачи класс явлений содержит явления, вообще неподобные между собой. Выделение из него подкласса подобных явлений осуществляется с помощью следующего условия.
Для подобия двух явлений необходимо и достаточно, чтобы численные значения безразмерных комбинаций, составленных из полного перечня определяющих параметров, образующих базу, в этих двух явлениях были одинаковы. Условия о постоянстве базы отвлеченных параметров, составленных из заданных величин, определяющих явление, наз. критериями подобия. В гидродинамике важнейшими критериями подобия являются Рейнольдса число, характеризующее соотношение между инерционными силами и силами вязкости, Маха число, учитывающее сжимаемость газа, и Фруда число, характеризующее соотношение между инерционными силами и силами тяжести. Основными критериями подобия процессов теплопередачи между жидкостью (газом) и обтекаемым телом являются: Прандтля число, характеризующее термодинамич. состояние среды; Нуссельта число, характеризующее интенсивность конвективного теплообмена между поверхностью тела и потоком жидкости (газа); Пекле число, характеризующее соотношение между конвективным и молекулярным процессами переноса тепла в жидкости; Стэнтона число, характеризующее интенсивность диссипации энергии в потоке жидкости или газа. Для распределения, тепла в твердом теле критериями подобия являются Фурье число, характеризующее скорость изменения тепловых условий в окружающей среде и скорость перестройки поля темп-ры внутри тела, и число Био, определяющее характер соответствия между температурными условиями среды и распределением температуры внутри тела. В процессах, изменяющихся с течением времени, основными критериями подобия, характеризующими одинаковость протекания процессов во времени, являются критерии гомохронности. В задачах аэрогидромеханики этот критерий наз. Струхаля числом. Критерием подобия механич. движения является Ньютона число. При изучении упругих деформаций критерием подобия является коэффициент Пуассона. Если условия подобия выполнены, то для фактич. расчета всех характеристик в натуре по данным о размерных характеристиках на модели необходимо знать переходные масштабы для всех соответствующих величин. Если явление определяется ппараметрами, из к-рых kимеют независимые размерности, то для величин с независимыми размерностями переходные масштабы могут быть произвольными и их нужно задать с учетом условий задачи, а при экспериментах - и с учетом условий опыта. Переходные масштабы для всех остальных размерных величин получаются из формул, выражающих размерности каждой размерной величины через размерности kвеличин с независимыми размерностями, для к-рых масштабы подсказаны условиями опыта и постановки задачи.
Напр., в задаче об установившемся обтекании тела несжимаемой вязкой жидкостью все безразмерные величины, характеризующие движение в целом, определяются тремя параметрами: углами a, b (направление поступательной скорости тела относительно его поверхности) и числом Рейнольдса R. Условия физич. подобия - критерии подобия - представляются соотношениями:
Число гомохронности. Пример применения Критерии подобия - безразмерные числа, составленные из размерных физ. величин, определяющих рассматриваемое физ. явление. Любая физ. величина представляет собой произведение численного значения на единицу измерения и, т. о., всегда зависит от выбора системы единиц измерения. Значения критерия подобия от единиц измерения не зависят. Равенство всех однотипных критериев для двух физ. явлений (процессов) или систем - необходимое и достаточное условие физ. подобия этих систем. Число гомохронности характеризует нестационарность процесса движения и его используют при изучении теплообмена в нестационарных (например, пульсирующих) потоках. Число Эйлера определяет подобие полей давления. В некоторых системах это число является однозначной функцией числа Рейнольдса. VT/L=Но, где V-характерная скорость, Т-характерное время изменения процесса, L-характерный линейный размер. Число Струхала— частный вид критерия гомохронности, применяемый в гидроаэромеханике. Число гомохронности Но и число Фурье Fo являются определяющими критериями для нестационарных процессов. Число, или критерий Фурье— один из критериев подобия нестационарных тепловых процессов. Характеризует соотношение между скоростью изменения тепловых условий в окружающей среде и скоростью перестройки поля температуры внутри рассматриваемой системы (тела), который зависит от размеров тела и коэффициента его температуропроводности: Fo = at0/l2, где а = l/rc — коэффициент температуропроводности, (l — коэффициент теплопроводности, r — плотность, с — удельная теплоёмкость), l — характерный линейный размер тела, t0 — характерное время изменения внешних условий. Поскольку критерии, устанавливающие связь между скоростями развития различных эффектов, называются критериями гомохронности, число Фурье является критерием гомохронности тепловых процессов, т.е. связывает времена различных эффектов.
Число Фруда. Пример применения Число́ Фру́да (), или критерий Фруда, — один из критериев подобия движения жидкостей и газов, является безразмерной величиной. Применяется в случаях, когда существенно воздействие внешних сил. Введено Уильямом Фрудом в 1870 году. Число Фруда в гидродинамике Число Фруда характеризует соотношение между силой инерции и внешней силой, в поле которой происходит движение, действующими на элементарный объём жидкости или газа: Fr=v2/gL где v— характерный масштаб скорости, g— ускорение, характеризующее действие внешней силы, L— характерный размер области, в которой рассматривается течение. Например, если рассматривается течение жидкости в трубе в поле силы тяжести, то под величиной g понимается ускорение свободного падения, под величиной v — скорость течения, а за L можно принять длину трубы или её диаметр. В судостроении используется другая версия числа Фруда - корень из выше указанного гидродинамического числа Фруда. Число Фруда позволяет сравнивать условия волнообразования для судов разного размера. Для больших водоизмещающих судов число Фруда обычно равно 0,2—0,3, а для малых глиссирующих судов оно, как правило, превышает 1, но обычно выбирается из диапазона 2—3. Также Число Фруда применяют при моделировании течений воды в открытых руслах и испытаниях моделей гидротехнических сооружений. Число Фруда в теплопередаче В теплопередаче критерий Фруда также характеризует соотношение между силой инерции и силой тяжести, но выражается иначе: Fr=gl/w2 где g — ускорение свободного падения, l— определяющий (характéрный) размер, w— скорость потока жидкости или газа. Чем больше число Fr, тем меньше влияние силы тяжести на свойства движения. Учитывая интервалы изменения длины L (102 – 2·106 м) и скорости V (10 - 50 м/с) и приближенно принимая g ≈ 10 м/с2, ω =7*10-5 1/с и v= 1,5*10-5 м2/с, для критериев подобия получаем следующие значения верхнего и нижнего пределов возможных значений числа Фруда: Верхний предел 502/10*1022=2,5 Нижний предел 10/2*7*10-5*2*106=4*10-2 Число отклонения от геострофичности. Пример применения V/2ωL=De V-характерная скорость, L-характерный размер, ω-угловая скорость Чем больше число De, тем меньше влияет на движение отклоняющая сила вращения Земли. При больших значениях числа De на свойства движения большое влияние оказывают си- лы инерции, определяемые конвективным членом в уравнениях движения. Учитывая интервалы изменения длины L (102 – 2·106 м) и скорости V (10 - 50 м/с) и приближенно принимая g ≈ 10 м/с2, ω =7*10-5 1/с и v= 1,5*10-5 м2/с, для критериев подобия получаем следующие значения верхнего и нижнего пределов возможных значений: Верхнего предела 50/2*7*10-5*102=4*103 Нижнего предела 10*102/1,5*10-5=7*107
Число Эйлера. Пример применения Число Эйлера (Eu) — безразмерный коэффициент, имеющий место в уравнениях Навье — Стокса, описывающий отношение между силами давления на единичный объём жидкости (или газа) и инерционными силами. Eu=Δp/v2ρ где ρ— плотность, Δр— перепад давления, расходуемый на преодоление гидравлического сопротивления, v— скорость.
Число Рейнольдса. Пример применения. Число Рейнольдса – один из критериев подобия (безразмерные величины, характеризующие соотношения различных сил, действующих в жидкости (газе). Число Рейнольдса используется в динамике до звуковых потоков (потоков со скор. меньшими скор. звука) и определяется по ф-ле скорости в рассматриваемом слое жидкости. Наиболее часто число Рейнольдса используется при изучении закономерностей движения жидкостей и газов в каналах в отсутствии вращения. Чем больше Re, тем меньше влияет на свойства движения сила вязкости. Значение числа Рейнольдса, при кот. ламинарный поток сменяется турбулентным, называют критическим числом Рейнольдса Число Re применяется в гидравлике (напр., вычисление гидравлического радиуса труб и каналов). 21. Определяющие и внутренне обусловленные критерии. Примеры. Критерии подобия делятся на 2 группы: а) Критерии подобия, содержащие, определяющие параметры, т. е. внешне обусловленные характерные величины и физические константы. Физическими константами жидкости являются характерная плотность и кинематический коэффициент вязкости. Угловая скорость вращения Земли и ускорение силы тяжести также относятся к определяющим параметрам. Наличие этих критериев накладывает дополнительные условия на внешне обусловленные величины. Действительно, движении будут подобны только тогда, когда внешне обусловленные величины удовлетворяют одновременно критериям, образованным из уравнений движения и из краевых условий. Иначе говоря, каждый такой критерий ограничивает возможность осуществления подобия движений и является, таким образом, определяющим. б) Критерии подобия, содержащие хотя бы одну из внутренне обусловленных величин, явл. неоопределяющими. Если осуществлены все усл. подобия, вытекающие из определяющих критериев и краевых условий, то эти критерии обязательно выполняются для всего класса подобных движений. Т. о., когда соответствующее безразмерное число определено для какого-то одного случая, то неопределяющий критерий представляет собой соотношение, связывающее характерные значения. При вычислении числа определяющих критериев необходимо соблюдать одно важное правило – критерии должны быть приведены к такой форме, чтобы каждая внутренне обусловленная величина встречалась лишь в одном из них. Очевидно, что эта всегда может быть достигнуто путем перемножения или деления критериев, содерж. одну и ту же внутренне обусловленную величину. Если это правило не соблюдено, то никаких заключений о том, какие критерии явл. определяющими, конечно, сделать нельзя. Для пояснения определ. и неопредел. критериев подобия разберем некоторые вопросы, связанные с моделированием обтекания горного массива установившимся воздушным потоком. Направим ось х по направлению невозмущенного потока, ось z по вертикали, и пусть вдали от массива u=u(z), v=0, w=0. Высоту препятствия в пункте с координатами х, у описываем ур-нием z=h(x,y) при х>0. Тогда условие «прилипания» запишетсяв виде: Из этих краевых условий следует, что при моделировании движения необх. воспроизвести в некоторых определенных соотношениях профиль горного массива и набегающий на препятствие поток, т.е. величины L и V в дан. случае явл. внешне обусловленными. Отсюда следует, что из 5 безразмерных критериев подобия определяющими будут три – совпадение чисел Фруда, Рейнольдса и отклонения ветра от геострофического. Если, например, задать определенный характерный размер модели, то соотношение L1/L2 явится известной величиной, то определяющими критериями будут все те же три числа – Fr, Re, De. Совпадение чисел Но будет выполняется автоматически, т. к. в случае установившегося движения период равен бесконечности, то никаких новых выводов отсюда сделать нельзя. Совпадение же чисел Еu в данном случае приводит к очень важному результату. Если определить из опыта разность давлений между двумя какими-то точками модели, то разность давлений в соответственных точках при естественном обтекании может быть найдена из соотношения Следовательно, неопределяющий критерий дает правила пересчета результатов опыта на натуру. Необходимо отметить, что такое соотношение критериев, когда Fг, Rе, Dе явлю определяющими, а Но и Еu неопределяющими критериями, имеет место в очень многих зад. гидромеханики. Однако в ряде метеорологических задач величина L оказывается не внешне, а внутренне обусловленным размером. Это приводит к коренному изменению определяющих критериев подобия. Скалярное произведение векторов. Пример в д. метеорологии. Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора а на проекцию другого вектора b на данный вектор а.
Из ф-лы следует, что Для любых векторов a, b и c и любого числа λ справедливы равенства: 1. 2. 3. 4. Если векторы
то их скалярное произведение может быть вычислено по формуле
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
Угол
дается формулой Векторное произведение векторов. Пример в динам. Метеорологии Если для определение физ величины. Кроме численного значения, необходимо указать направление в пространстве, то такие величины называют векторами. Векторным произведением АхВ двух векторов называется вектор С = А*В (рис.), направленный перпендикулярно плоскости векторов-сомножителей в ту сторону, откуда поворот от первого сомножителя ко второму на меньший угол против хода часовой стрелки и равный по величине площади параллелограмма, построенного на этих векторах, т.е. |C|=|A*B|=ABsin(A,B)
Векторное произведение векторов определяется следующими условиями: 1). Модуль вектора |С| равен ABsin(A,B), где (A,B) - угол между векторами A и B; 2). Вектор |C| перпендикулярен к каждому из векторов A и B; 3). Направление вектора |С| соответствует «правилу правой руки». Это означает, что если векторы A, B и |С| приведены к общему началу, то вектор |С| должен быть направлен так, как направлен средний палец правой руки, большой палец которой направлен по первому сомножителю (то есть по вектору A), а указательный - по второму (то есть по вектору B). Векторное произведение зависит от порядка сомножителей, именно: Необходимое и достаточное условие параллельности векторов имеет вид: А*В=0. Если система координатных осей правая и векторы А и В заданы в этой системе своими координатами:
то векторное произведение вектора А на вектор В определяется формулой
Пример в динамич метеорологии: Такие векторы, направление которых устанавливается соглашением и которые изменяют свое направление при замене правой системы координат на левую, называются аксиальными, например момент силы и угловая скорость. Векторы, направление которых определяется физическим смыслом и которые не меняют своего направления при изменении системы координат, называют полярными, например сила и скорость.
24. Понятие тензора. Пример в динам. Метеорологии Те́нзор (от лат. tensus, «напряженный») — объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры, векторы, билинейные формы и т.п. Скаляр или тензор нулевого ранга — физическая величина, полностью определяемая в любой координатной системе одним числом (или функцией), которое не меняется при изменении пространственной системы координат. Скаляр имеет одну компоненту. Таким образом, если ф — значение скаляра в одной системе координат, а ф' — в другой, то ф'=ф. Векторы — величины более высокого ранга по сравнению со скалярами; они могут быть названы тензорами 1-го ранга. Тр
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.235.107 (0.014 с.) |

 где — v2пер переносная скорость, a rᵩ — расстояние частицы до земной оси.
где — v2пер переносная скорость, a rᵩ — расстояние частицы до земной оси. где Т* — сутки, то на расстоянии rᵩ от оси переносная скорость равна w rᵩ,. Величина же rᵩ, равна rᵩ = r cosᵩ (r — расстояние частицы от центра земли). Учитывая все это, формулу для центробежного ускорения можем написать так:
где Т* — сутки, то на расстоянии rᵩ от оси переносная скорость равна w rᵩ,. Величина же rᵩ, равна rᵩ = r cosᵩ (r — расстояние частицы от центра земли). Учитывая все это, формулу для центробежного ускорения можем написать так: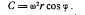 , где w2 = 7,297 • 10-5 1/с - угловая скорость вращения Земли; r — расстояние частицы от центра земли, ᵩ - географическая широта.
, где w2 = 7,297 • 10-5 1/с - угловая скорость вращения Земли; r — расстояние частицы от центра земли, ᵩ - географическая широта.
 в декартовой системе координат
в декартовой системе координат  (т.е.
(т.е.  ) вводят следующим образом. Рассматривают бесконечно малый объём тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади
) вводят следующим образом. Рассматривают бесконечно малый объём тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади  . На каждой грани
. На каждой грани  . Если обозначить проекции этих сил на оси
. Если обозначить проекции этих сил на оси 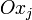 как
как  , то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:
, то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:
 здесь суммирования нет. Компоненты
здесь суммирования нет. Компоненты  ,
, 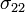 ,
,  , обозначаемые также как
, обозначаемые также как 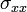 ,
,  ,
,  — это нормальные напряжения, они представляют собой отношение проекции силы
— это нормальные напряжения, они представляют собой отношение проекции силы  и т.д.
и т.д. ,
,  ,
,  , обозначаемые также как
, обозначаемые также как  ,
,  ,
,  — это касательные напряжения, они представляют собой отношение проекции силы
— это касательные напряжения, они представляют собой отношение проекции силы  и т.д.
и т.д. (1)
(1)
 ).Тогда из n величин можно составить только n-kнезависимых безразмерных комбинаций. Все искомые безразмерные характеристики явления можно рассматривать как функции от этих п-k независимых безразмерных комбинаций, составленных из определяющих параметров. Среди всех безразмерных величин, составленных из определяющих характеристик явления, всегда можно указать нек-рую базу, т. е. систему безразмерных величин, к-рые определяют собой все остальные.
).Тогда из n величин можно составить только n-kнезависимых безразмерных комбинаций. Все искомые безразмерные характеристики явления можно рассматривать как функции от этих п-k независимых безразмерных комбинаций, составленных из определяющих параметров. Среди всех безразмерных величин, составленных из определяющих характеристик явления, всегда можно указать нек-рую базу, т. е. систему безразмерных величин, к-рые определяют собой все остальные.
 где U – скорость потока, L - характерный линейный размер теч. (в качестве такового может выступать как верт. размер Н, так и гориз. размер L в зависимости от специфики рассматриваемого течения и необходимости разделения линейных размеров по вертикали и горизонтали), vm - кинематическая вязкость жидкости (традиционно (при рассмотрении ламинарных течений) под этой величиной понимают молекулярную вязкость, но в метеорологии, где изучаются турбулизованные течения, под ней чаще всего подразумевают «турбулентный» аналог ). Число Рейнольдса (названо в честь англ. физика Осборна Рейнольдса) характеризует отношение между силами инерции и силами трения в потоке жидкости. Весьма часто используются другие формулировки числа Рейнольдса, напр.,
где U – скорость потока, L - характерный линейный размер теч. (в качестве такового может выступать как верт. размер Н, так и гориз. размер L в зависимости от специфики рассматриваемого течения и необходимости разделения линейных размеров по вертикали и горизонтали), vm - кинематическая вязкость жидкости (традиционно (при рассмотрении ламинарных течений) под этой величиной понимают молекулярную вязкость, но в метеорологии, где изучаются турбулизованные течения, под ней чаще всего подразумевают «турбулентный» аналог ). Число Рейнольдса (названо в честь англ. физика Осборна Рейнольдса) характеризует отношение между силами инерции и силами трения в потоке жидкости. Весьма часто используются другие формулировки числа Рейнольдса, напр., 
 где
где  - разность скорости потока на границах рассматриваемой области,
- разность скорости потока на границах рассматриваемой области,  - градиент
- градиент . Если
. Если  , то течение происходит в ламинарном режиме, а если
, то течение происходит в ламинарном режиме, а если 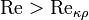 , то возможно возникновение турбулентности. Физически это означает, что силы трения при возрастании сил инерции не в состоянии поддерживать динамическое равновесие, свойственное ламинарному потоку, и оно сменяется новой формой динамического равновесия, при кот. структура течений становится зависящей от времени.
, то возможно возникновение турбулентности. Физически это означает, что силы трения при возрастании сил инерции не в состоянии поддерживать динамическое равновесие, свойственное ламинарному потоку, и оно сменяется новой формой динамического равновесия, при кот. структура течений становится зависящей от времени.

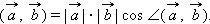

 , если
, если  - острый угол,
- острый угол,  , если
, если  в том и только в том случае, когда векторы
в том и только в том случае, когда векторы  и
и  перпендикулярны (в частности,
перпендикулярны (в частности,  или
или  ).
). причем
причем 
 (переместительный закон).
(переместительный закон). (распределительный закон).
(распределительный закон). (сочетательный закон).
(сочетательный закон). ,
,  ,
,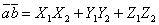 .
. .
. , или в координатах
, или в координатах 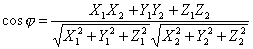 .
.
 .
. ,
, 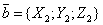 ,
,
 Или С=А*В=(A1i1+A2i2+A3i3)*(B1i1+B2i2+B3i3)=i1(A2B3-A3B2)+i2(A3B1-A1B3)+i3(A1B2-A2B1)
Или С=А*В=(A1i1+A2i2+A3i3)*(B1i1+B2i2+B3i3)=i1(A2B3-A3B2)+i2(A3B1-A1B3)+i3(A1B2-A2B1)



