
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Матрицы и действия с нимиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
Введение §1. Основные определения. Виды матриц Определение матрицы m ´ n Элементы матрицы Квадратная матрица Порядок матрицы Матрица-строка Матрица-столбец Нулевая матрица Главная диагональ матрицы Треугольная матрица Диагональная матрица Единичная матрица §2. Действия над матрицами 1. Равенство матриц 2. Транспонирование 3. Сложение матриц 4. Умножение матрицы на число 5. Умножение матриц
§ 1. Определение матрицы. Виды матриц
Матрицей размером m × n называется совокупность m · n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Этутаблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В. В общем виде матрицу размером m × n записывают так
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a 23 – элемент стоит во 2-ой строке, 3-м столбце. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1. Матрица, в которой число строк не равно числу столбцов, называется прямоугольной матрицей. В примерах это первая матрица и третья. Различаются также матрицы, имеющие только одну строку или один столбец. Матрица, у которой всего одна строка Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается (0), или просто 0. Например,
Главной диагональю матрицы называют совокупность ее элементов, у которых индексы состоят из одинаковых чисел: Для квадратной матрицы главная диагональ идет из левого верхнего в правый нижний угол.
Матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например,
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид:
§ 2. Действия над матрицами
1. Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij.
a 21 = b 21 и a 22 = b 22.
2. Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером).
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием. Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают А'. Связь между матрицей A и её транспонированной матрицей можно записать в виде Например. Найти матрицу, транспонированную данной.
3. Сложение матриц Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц одинаковой размерности A и B называется матрица C, которая определяется по правилу, например,
Примеры. а) Найти сумму матриц
б) Следующую сумму найти нельзя, т.к. размеры матриц различны.
в) Легко проверить, что сложение матриц подчиняется следующим законам: 1) коммутативному: A + B = B + A; 2) ассоциативному: (A+B) + C = A + (B+C).
4. Умножение матрицы на число Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица С, которая определяется по правилу
Для любых чисел a и b и для любых матриц A и B выполняются равенства: 1) 2) 3) Примеры.
б) Найти матрицу 2 A – B, если
в) Найти C = –3 A + 4 B, если
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
5. Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц-сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A на матрицу B называется новая матрица C = AB, элементы которой составляются следующим образом:
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c 13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы. В общем случае, если мы умножаем матрицу A = (aij) размера m × n на матрицу B = (bij) размера n × p, то получим матрицу C размера m × p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i -ой строки матрицы A на соответствующие элементы j -го столбца матрицы B и их сложения. Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат. Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
Примеры. 1) Пусть
Найти элементы c 12, c 23 и c 21 матрицы C.
2) Найти произведение матриц.
3) Пусть
Найти АВ и ВА.
4) Пусть
Найти АВ и ВА.
Эти простые примеры показывают, что матрицы, вообще говоря, при умножении матрицы нельзя переставлять местами друг с другом, т.е. A ∙ B ≠ B ∙ A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей. Таким образом, умножение матриц 1) НЕ коммутативно: A ∙ B ≠ B ∙ A; Можно проверить, что умножение матриц: 2) ассоциативно: (AB) C = A (BC); 3) дистрибутивно: (A + B) C = AC + BC. Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE = EA = A. Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице. Например, для матриц
Линейная алгебра
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.72.220 (0.011 с.) |



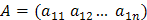 , называется матрицей – строкой (или стрóковой), а матрица, у которой всего один столбец
, называется матрицей – строкой (или стрóковой), а матрица, у которой всего один столбец  , матрицей – столбцом.
, матрицей – столбцом.
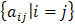 . Например, а 11, а 22, а 33 и т.д.
. Например, а 11, а 22, а 33 и т.д.



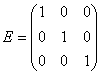
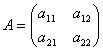
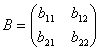


 .
.



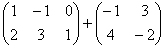
 .
. .
.

 .
.
 ,
,  .
.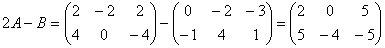 .
.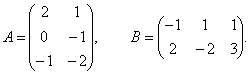 .
. .
.




 нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.









