Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гипотеза о нормальном законе распределения
Проверим гипотезу о том, что длина слов из примера распределена по нормальному закону. При нормальном распределении необходимо знать два параметра – математическое ожидание и среднее квадратическое отклонение. По условию параметры распределения оцениваются по выборке, тогда математическое ожидание принимается равным среднему выборочному, а среднее квадратическое отклонение – равным корню из несмещенной оценки дисперсии. Ранее мы нашли, что Таким образом, проверяется гипотеза Н 0: ξ ~ N (4,5; 2,946) при уровне значимости α = 0,05. Воспользуемся критерием Пирсона: пусть по выборке оцениваются т параметров функции распределения F (x). Тогда гипотеза о том, что генеральная совокупность имеет функцию распределения F (x) не согласуется с данными эксперимента, если выборочное значение статистики c2 удовлетворяет неравенству
где ni – частота попадания элементов выборки в i -й интервал, pi – теоретические вероятности; п – объем выборки;
Для вычисления выборочного значения статистики c2 составим расчетную таблицу (Таблица 3). При заполнении 1-го, 2-го и 3-го столбцов воспользуемся результатами частотной табуляции (Таблица 1) с небольшими изменениями: поскольку проверяется гипотеза о нормальности, первый интервал следует расширить влево до –¥, а последний – вправо до +¥. Таблица 3
Теперь вычислим теоретическую вероятность попадания случайной величины в каждый интервал. Для нормально распределенной случайной величины вероятность попадания в интервал (a; b) находится по формуле:
где а – математическое ожидание, s – среднее квадратическое отклонение, Ф – функция распределения стандартной нормальной случайной величины N (0; 1). В нашем примере a = 4,5 и s = 2,946. Значения функции Ф(х) находят по таблице (Приложение 1)[16] или с помощью специальных программных средств (например, в Excel можно использовать встроенную статистическую функцию НОРМСТРАСП(х))[17]:
1) p 1= = 0,3053 – 0 = 0,3053 2) p 2=
3) p 3=
4) p 4=
5) p 5=
6) p 6=
Полученные результаты заносим в таблицу. Для проверки правильности суммируем данные четвертого столбца. Должна получиться единица. В нашем случае проверка выполняется. Следующий столбец получается умножением 4-го столбца на объем выборки, в нашем случае на 20. Правильность расчета ожидаемых частот также проверяем суммированием: должно получиться число, равное объему выборки, т.е. 20. В полученной таблице ожидаемые частоты в трех последних интервалах слишком малы. Считается, что выборка хорошо сгруппирована для применения критерия Пирсона, если для всех интервалов п·pi ³ 5. Когда это условие не выполняется, интервалы объединяются в один. В нашем примере необходимо объединить три последних интервала, при этом число интервалов разбиения становится равным 4 (r = 4). При этом наблюдаемая частота нового интервала равна сумме наблюдаемых частот объединенных интервалов: 1 + 1 + 1 = 3; и ожидаемая частота – сумме ожидаемых частот: 2,695 + 0,993 + 0,274 = 3,962. На основе Таблицы 3 сформируем новую расчетную таблицу (Таблица 4), в которой запишем 4 получившихся интервала, их наблюдаемые и ожидаемые частоты. Дополнительно высчитаем для каждого интервала величины 1-й интервал 2-й интервал 3-й интервал 4-й интервал Таблица 4
Сумма всех элементов последнего столбца Таблицы 7 и есть значение статистики Для применения критерия Пирсона найдем
Применяя критерий Пирсона, запишем:
Полученное неравенство неверно, т.е. выборочное значение статистики c2 не удовлетворяет неравенству Заметим, что исследовалась небольшая выборка (п = 20) и в последнем интервале ожидаемая частота оказалась все-таки меньше 5. Применяя критерий Пирсона для проверки гипотезы о законе распределения, следует брать выборку большего объема (п ≥ 50) и группировать выборку так, чтобы ожидаемые частоты были не меньше 5.
Литература
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие – 11-е изд., перераб. – М.: Высшее образование, 2006 2. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч.: Учеб. пособие для вузов / П.Е.Данко, А.Г.Попова, Т.Я.Кожевникова. – 6-е изд. – М.: ООО «Издательство Оникс»: ООО Издательство «Мир и Оразование», 2006 3. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом приложении: Учебник. – 4-е изд., испр. – М.: Дело, 2003 4. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. Пособие/ под ред. проф. Н.Ш.Кремера. – М.: Высшее образование, 2009 5. Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями: Учебное пособие. – Москва: ИКЦ «МарТ»; Ростов-н/Д: Издательский центр «МарТ», 2005
Электронные источники
6. Лекции по теории вероятностей и математической статистике, А.А.Соловьев / файл формата pdf
Книги с сайта www.knigafund.ru/ Электронная библиотечная система «КнигаФонд»
1. Высшая математика: учебное пособие Автор: Малыхин В. 2. Высшая математика: конспект лекций Автор: Березина Н.А. 3. Задачи с решениями по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями: Учебное пособие Авторы: Шапкин А.С., Шапкин В.А. 4. Теория вероятности и математическая статистика: конспект лекций Автор: Щербакова Ю.В.
Приложение 1 Функция распределения Ф(х) стандартной нормальной случайной величины N (0; 1).
Квантили χ2 p (k) распределения «хи-квадрат»
Федеральное государственное образовательное учреждение высшего профессионального образования «Псковский юридический институт Федеральной службы исполнения наказаний»
Факультет подготовки государственных и муниципальных служащих
Решение задач линейного программирования
Методическое пособие по дисциплине «МАТЕМАТИКА»
для заочной формы обучения по специальности 030504.65 – «Государственное и муниципальное управление»
Преподаватель: Кочерова Ю.Я.
Псков Решение задач линейного программирования
Геометрический метод. Геометрическим методом может быть решена задача в стандартной форме с двумя переменными (п = 2). К такой форме может быть сведена и каноническая задача с ограничениями в виде уравнений, когда п – т = 2, где п – число переменных, т – число уравнений. Рассмотрим решение задачи линейного программирования геометрическим методом на примере.
Пример. Задача об использовании ресурсов. Для изготовления двух видов продукции Р 1 и Р 2 используют четыре вида ресурсов S 1, S 2, S 3 и S 4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице.
Прибыль, получаемая от реализации единицы продукции Р 1 и Р 2, составляет 2 и 3 рубля соответственно. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Решение. 1. Составим экономико-математическую модель задачи. Обозначим х 1 и х 2 – число единиц продукции соответственной Р 1 и Р 2, запланированных к производству. Для их изготовления потребуется соответственно таблице данных:
Т.к. потребление ресурсов не должно превышать их запасов, составляющих соответственной 18, 16, 5 и 21 единицу, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
Суммарная прибыль F составит: 2 х 1 рублей – от реализации продукции Р 1 и 3 х 2 рублей – от реализации продукции Р 2, т.е.
 .
Итак, экономико-математическая модель задачи: найти такой план выпуска продукции Х = (х 1; х 2), удовлетворяющий системе (1.1 ) и условию (1.2), при котором функция (1.3) принимает максимальное значение. При записи решения это оформляется кратко:
2. Построим множество решений (многоугольник решений) системы ограничений. Для этого на координатной плоскости, где горизонтальная ось – Ох 1, а вертикальная – Ох 2, построим последовательно множество решений каждого неравенства (Рис. 1). Рассмотрим первое неравенство
Построенная прямая (на рисунке отмечена знаком ) разбивает плоскость на две полуплоскости, одна из которых является решением первого неравенства. Для определения искомой полуплоскости рекомендуется задать произвольную (контрольную) точку, не лежащую на границе полуплоскостей (т.е. не лежащую на построенной прямой). Если неравенство выполняется в контрольной точке, то оно выполняется во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости. И наоборот. В нашем примере в качестве контрольной точки удобно взять начало координат – точку О (0; 0). Подставим ее координаты в первое неравенство:
Получили верное неравенство, значит, решением первого неравенства является та полуплоскость, в которой находится точка О (0; 0), а это часть плоскости, которая находится ниже построенной прямой (на рисунке эту полуплоскость обычно обозначают штриховкой с одной стороны прямой).
Рис.1.
Рассмотрим второе неравенство
Для определения искомой полуплоскости, как и в первом случае, возьмем точку О (0; 0). Подставим ее координаты во второе неравенство:
Получили верное неравенство, значит, решением второго неравенства является та полуплоскость, в которой находится точка О (0; 0), а это часть плоскости, которая находится ниже построенной прямой. На рисунке вторую прямую отметим знаком ‚. Рассмотрим третье неравенство
Получили верное неравенство, значит, решением третьего неравенства является та полуплоскость, в которой находится точка О (0; 0), а это часть плоскости, которая находится ниже построенной прямой. Рассмотрим четвертое неравенство
Получили верное неравенство, значит, решением четвертого неравенства является та полуплоскость, в которой находится точка О (0; 0), а это часть плоскости, которая находится левее построенной прямой. Дополнительное условие системы ограничений Область плоскости, где пересекаются все решения отдельных неравенств (на рисунке отмечена желтым цветом), является множеством решений системы ограничений нашей задачи. Обозначим вершины полученного многоугольника буквами А, В, С, D и E. Шестиугольник ОАВСDE есть искомый многоугольник решений системы ограничений. 3. Рассмотрим функцию прибыли 4. Проведем через начало координат прямую, перпендикулярную вектору Обозначим на графике прямую, проходящую через точку С, равенством 5. Координаты точки С являются оптимальным решением (оптимальным планом). Точка С – это точка пересечения прямых и ‚, следовательно, ее координаты определяются системой уравнений:
Решая систему, получим х 1 = 6, х 2 = 4, т.е. Х опт. = (6; 4). Подставим найденные координаты в функцию прибыли
Вывод. Максимальная прибыль в 24 рубля достигается при производстве 6 единиц продукции Р 1 и 4 единиц продукции Р 2.
Симплексный метод. Симплексный метод – метод последовательного улучшения решения (плана) и нахождения оптимального решения (плана). Он заключается в том, что в начале находится любое допустимое базисное решение, а затем это решение целенаправленно улучшается. Симплексный методом является универсальным методом, которым можно решить любую задачу линейного программирования. Рассмотрим решение задачи линейного программирования симплексным методом на примере.
Пример. Решить симплексным методом задачу об использовании ресурсов. Решение. Решение задачи будем оформлять в виде симплексных таблиц. Ранее мы уже составили экономико-математическую модель этой задачи:
По условию применения симплексного метода, система ограничений должна быть приведена к системе линейных уравнений. Если (как в нашем случае) ограничительные условия заданы неравенствами, то их преобразуют в равенства путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих) переменных. Добавим к левой части каждого неравенства нашей системы ограничений соответствующую балансовую переменную: в первом неравенстве – х 3, во втором неравенстве – х 4, в третьем – х 5 и в четвертом – х 6. Получим:
Условие неотрицательности всех переменных от х 1 до х 6 можно записать кратко:
запишем в виде
Заполним исходную таблицу (Таблица 1). Заполнение таблицы начинаем со столбцов «х 1» – «х 6» и «Свободные члены», занося в таблицу коэффициенты при соответствующих переменных[19] и свободные члены из системы ограничений (1.4). При этом коэффициенты в столбцах х 3, х 4, х 5 и х 6 образуют единичную матрицу, следовательно, именно эти четыре переменные будут базисными в исходной таблице. Запишем эти переменные в столбец «Базисные переменные» так, чтобы на пересечении одноименных строки и столбца (например, строка «х 3» и столбец «х 3») стояла единица. Последняя строка симплексной таблицы называется индексной. В ней записываем коэффициенты при соответствующих переменных функции прибыли из уравнения (1.5). Элементы последней строки называют оценками. Исходная таблица заполнена. Таблица 1
Шаг1. Выясним, имеются ли в последней (индексной) строке отрицательные числа (оценки). Таких чисел два: -2 и -3. Выбираем одно из них, например, -3, и просматриваем соответствующий столбец (столбец «х 2»)[20]. В столбце «х 2» есть три положительных элемента: 3, 1 и 1. Делим на эти числа соответствующие свободные члены:
Получили, что наименьшим является третье частное, т.е. частное элементов строки «х 5», следовательно, эта строка становиться разрешающей. Выделим в таблице разрешающую строку и разрешающий столбец. Элемент на их пересечении называется разрешающим элементом. Он равен 1. Начнем составление следующей таблицы (Таблица 2). В столбце «Базисные переменные» вместо элемента х 5 из разрешающей строки пишем элемент х 2 из разрешающего столбца. Теперь базисными переменными являются х 3, х 4, х 2 и х 6. На месте третьей строки новой таблицы (строка «х 2») записываем элементы разрешающей строки Таблицы 1, деленные на разрешающий элемент. Т.к. у нас разрешающий элемент равен 1, то разрешающая строка переписывается без изменений. К каждой из остальных строк прибавляем разрешающую строку, умноженную на такое число, чтобы в клетках разрешающего столбца получались нули. Например, умножим разрешающую строку Таблицы 1 на -3 и сложим с первой строкой этой таблицы. Результат запишем в первую строку Таблицы 2: столбец «х 1»: столбец «х 2»: столбец «х 3»: столбец «х 4»: столбец «х 5»: столбец «х 6»: столбец «Свободные члены»: Далее умножим разрешающую строку Таблицы 1 на -1 и сложим со второй строкой этой таблицы. Результат запишем во вторую строку Таблицы 2. Четвертую строку оставляем без изменений, т.к. в соответствующей клетке разрешающего столбца уже стоит 0. И, наконец, разрешающую строку Таблицы 1 умножим на 3 и сложим с последней (индексной) строкой этой таблицы. Результат запишем последнюю (индексную) строку Таблицы 2. Таблица 2
Шаг 2. Выясним, имеются ли в последне
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 677; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.119.199 (0.176 с.) |
и 
, тогда 
.
(r – m – 1) – квантиль порядка 
«хи-квадрат» распределения с k = r – m –1 степенями свободы.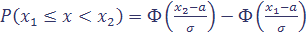
,
.
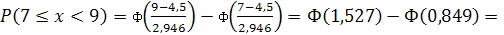
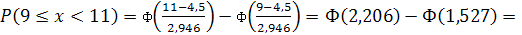
и результат запишем в новый столбец:
;
;
;
.
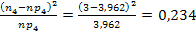. Таким образом, получили 
.
(r – m – 1). В нашем примере уровень значимости a = 0,05, тогда 1– a = 0,095. Число интервалов в итоге оказалось равным r = 4, а т = 2, т.к. по выборке оцениваются 2 параметра функции распределения, а именно математическое ожидание и среднее квадратическое отклонение, тогда r – m – 1 = 4 – 2 – 1 = 1. Таким образом, требуется определить квантиль порядка 
«хи-квадрат» распределения с k = 1 степенями свободы. Эту величину можно найти по таблице (Приложение2) или с помощью специальных программных средств (например, в Excel можно использовать встроенную статистическую функцию ХИ2ОБР(вероятность; степени свободы)[18]):
.
.
, следовательно, нулевая гипотеза Н 0: ξ ~ N (4,5; 2,946) не противоречит экспериментальным данным, а значит, не отвергается. Иными словами, с ошибкой 5% (или с вероятностью 95%) можно утверждать, что длина слов в книге «Винни-Пух и все-все-все» распределена по нормальному закону.
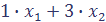единиц ресурса S 1;
единиц ресурса S 2;
единиц ресурса S 3;
единиц ресурса S 4.
.
при ограничениях
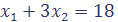
. Построим по двум точкам прямую, которая задается аналогичным равенством:
. Построим по двум точкам прямую, которая задается аналогичным равенством:
. Соответствующее равенство 
задает на плоскости горизонтальную прямую, походящую через точку (0;5). Построим эту прямую на координатной плоскости, обозначив символом ƒ. Для определения искомой полуплоскости также можно взять точку О (0; 0). Подставим ее координаты в третье неравенство:
. Оно эквивалентно неравенству 
. Соответствующее равенство 
задает на плоскости вертикальную прямую, походящую через точку (7; 0). Построим эту прямую на координатной плоскости, обозначив символом „. Для определения искомой полуплоскости опять возьмем точку О (0; 0). Подставим ее координаты в четвертое неравенство:
с началом в точке О (0; 0) и концом в точке (2; 3). Этот вектор является градиентом и показывает направление возрастания значений функции 
. Обозначим построенную прямую равенством 
. Далее, перемещая эту прямую параллельно самой себе в направлении вектора 
, т.к. именно в этой точке функция 
.
.
.
.
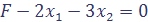. Среди полученных частных выбираем наименьшее: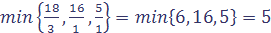
.
;
;
;
;
.
