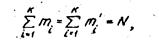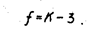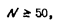Кривые F-распределения Фишера

Рис.1.3

Если окажется, что нулевая гипотеза справедлива, т.е. генераль­ные дисперсии одинаковы, то различие несмещенных оценок дисперсий незначимо и объясняется случайнымипричинами, в частности случайным отбором объектов выборки. Например, если различие несмещенных оценок дисперсий результатов измерений, выполненных двумя приборами, оказа­лось незначимым, то приборы имеют одинаковую точность.

Если нулевая гипотеза будет отвергнута, т.е. генеральные диспер­сии неодинаковы, то различие несмещенных оценок дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны. Например, если разли­чие _________________ результатов измерений, произведенных двумя приборами, оказалась значимым, то точность приборов различна.

 

Критерий Кохрэна

G -критерий Kохрэна применяется для оценки однородности несмещенных оценок дисперсий, вычисленных по одинаковому чис­лу N наблюдений. При этом генеральные совокупности должны быть распределены нормально. Критерий формируется как отношение максимальной из сравниваемых оценок дисперсий к сумме всех K дисперсий;

Если G<G _кр=G_q,f1,f2, то оценки дисперсий признаются однородными или, другими словами, различаются незначимо. В этом слу­чае с уровнем значимости q ммнимается нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: _____________________________________________.Числа степе­ней свободы числителя f1 и знаменателя f2 определяются условиями

Если требуется оценить генеральную дисперсию, то при условии од­нородности оценок дисперсий целесообразно принять в качестве ее оцен­ки среднее арифметическое несмещенных оценок дисперсий

Критерий Пирсона

Нормальный закон распределения характеризуется плотностью вероят­ности вида

 

где M{X}, ____ — соответственно математическое ожидание и диспер­сия случайной величины. согласованности изучаемого распределения с нормальным

Для проверки гипотезы о соответствии, экспериментального закона распределения случайной величины нормальному применяют критерий Пир­сона или, как его иначе называют, критерий X² (хи-квадрат),так как принятие и отклонение гипотезы основаны на X² -распределении.

Использование критерия Пирсона основано на сравнении эмпиричес­ких (наблюдаемых) ___ и теоретических (вычисленных в предположении нормального распределения) _____ частот. Обычно ____ и _____ различны.

Возможно, что расхождение случайно (незначимо) и объясняется малым числом наблюдений, способом их группировки Или другими причина­ми. Возможно, что расхождение частот неслучайно (значимо) и объясня­ется тем, что теоретические частоты вычислены, исходя из неверной ги­потезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный ранее вопрос. Однако, как и любой статистический критерий, он не доказывает справедливость гипотезы, а лишь устанавливает при принятом уровне значимости q ее согласие или несогласие с данными наблюдений.

Пусть по выборке объема ___ получено эмпирическое распределение.

Допустим, в предположении нормального распределения генеральной совокупности, вычислены теоретические частоты _____. При уровне значимости q требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы принимается слу­чайная величина

или

где К- число интервалов (вариант).

Эта величина случайная, так как в различая опытах она принимает различные, заранее неизвестные значения. Чем меньше различаются эмпирические и теоретические частоты, тем меньше значение критерияи, следовательно, он в известной мере характеризует близость эмпири­ческого и теоретического распределений. Возведением в квадрат разнос­тей частот устраняется возможность взаимного погашения положительных и отрицательных разностей.

При неограниченном возрастании объема выборки (_________) закон распределения случайной величины, независимо от того, какому за­кону распределения подчинена генеральная совокупность, стремится к за­кону распределения X² с f степенями свободы. Поэтому случайная ве­личина обозначена X², а сам критерий называют критерием сог­ласия "хи квадрат".

Число степеней свободы находят по равенству f=K-1-l где l- число параметров предполагаемого распределения, которые оце­нены по данным выборки, а l вызвана тем, что имеется дополнитель­ное ограничение:

т.е.- Теоретическое число элементов совокупности должно быть равно фак­тическому числу элементов.

Поскольку в данном случае, предполагаемое распределение является нормальным, nо оценивают два параметра (математическое ожидание и среднеквадратическое отклонение), поэтому l=2, и число степеней свободы

Еслирасчетное (наблюдаемое)значение критерия оказалось меньше критического _____ которое находят по таблицам, для соответствующего уровня значимости q и числа степеней свободы, т.е. если

то нет оснований отвергнуть нулевую гипотезу о нормальности распреде­ления. В противном случае (при ___________) нулевая гипотеза отверга­ется.

При проверке гипотезы о нормальности распределения существует правило, согласно которому общее количество элементов выборки должно быть

а число элементов, попавших в любой i-и интервал (т.е. значения эмпи­рических частот ____),должно быть ___________________________

Если в крайние интервалы попадает меньшее число элементов, то они объединяются ссоседними интервалами. Внутренние интервалы объеди­нять запрещается. Общее число интервалов К, оставшихся после объеди­нения, должно удовлетворять условию _____________

Иначе число степеней, свободы f окажется равным нулю, и гипо­тезу невозможно будет проверить.

В целях контроля вычислений формулу целесообразно преобра­зовать к виду

Если ­­­­_________, то нет оснований отвергнуть нулевую гипоте­зу. Т.е., расхождение эмпирических и теоретических частот незначимо. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.