
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор меры центральной тенденцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Каждая мера центральной тенденции обладает характеристиками, которые делают ее ценной в определенных условиях. Для номинативных данных, разумеется, единственной подходящей мерой центральной тенденции является мода, или модальная категория - та града-ция номинативной переменной, которая встречается наиболее часто. Для порядковых и метрических переменных, распределение которых унимодальное и симметричное, мода, медиана и среднее совпадают. Чем больше отклонение от симметричности, тем больше расхождение между значениями этих мер центральной тенденции. По этому расхождению можно судить о том, насколько симметрично или асимметрично распределение. Наиболее очевидной и часто используемой мерой центральной тенденции является среднее значение. Но его использование ограничивается тем, что на величину среднего влияет каждое отдельное значение. Если какое-нибудь значение в группе увеличится на с, то среднее увеличится на с/N Таким образом, среднее значение весьма чувствительно к «выбросам» - экстремально малым или большим значениям переменной. На величину моды и медианы величина каждого отдельного значения не влияет. Например, если в группе из 20 измерений цеременной наибольшее значение утроится по величине, то не изменится ни мода, ни медиана. Величина среднего при этом заметно изменится. Иначе говоря, мода и медиана не чувствительны к «выбросам».
Если 9 человек имеют месячный доход от 5000 до 6000 рублей, со средним 5600 рублей, а доход десятого составляет 15000 рублей, то средний доход для этих 10 человек составит 6540 рублей. Эта цифра не позволяет судить о всей группе, и в качестве меры центральной тенденции следовало бы избрать медиану или моду. Меры центральной тенденции чаще всего используются для сравнения групп по уровню выраженности признака. Если исследователь при этом сомневается, какую меру использовать, то можно дать простые советы. Выборочные средние можно сравнивать, если выполняются следующие условия: · группы достаточно большие, чтобы судить о форме распределения; · распределения симметричны; · отсутствуют «выбросы». Если хотя бы одно из перечисленных условий не выполняется, то следует ограничиться модой и медианой. Альтернативой является «сквозное» ранжирование представителей сравниваемых групп и сравнение средних, вычисленных для рангов этих групп. КВАНТИЛИ РАСПРЕДЕЛЕНИЯ Помимо мер центральной тенденции в психологии широко используются меры положения, которые называются квантилями распределения. Квантиль — это точка на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на две группы с известным соотношением их численности. С одним из квантилей мы уже знакомы — это медиана. Это значение признака, которое делит всю совокупность измерений на две группы с равной численностью. Кроме медианы часто используются процентили и квартили. Процентили {Percentiles) — это 99 точек — значений признака (Р1..., Р99), которые делят упорядоченное (по возрастанию) множество наблюдений на 100 частей, равных по численности. Определение конкретного значения про-центиля аналогично определению медианы. Например, при определении 10-го процентиля, Р10, сначала все значения признака упорядочиваются по возрастанию. Затем отсчитывается 10% испытуемых, имеющих наименьшую выраженность признака. Р10будет соответствовать тому значению признака, который отделяет эти 10% испытуемых от остальных 90%. Квартили (Quartlles) — это 3 точки — значения признака (Р2$, JPso» Лз)> которые делят упорядоченное (по возрастанию) множество наблюдений на 4 равные по численности части. Первый квартиль соответствует 25-му процентилю, второй — 50-му процентилю или медиане, третий квартиль соответствует 75-му процентилю. Процентили и квартили используются для определения частоты встречаемости тех или иных значений (или интервалов) измеренного признака или для выделения подгрупп и отдельных испытуемых, наиболее типичных или нетипичных для данного множества наблюдений. МЕРЫ ИЗМЕНЧИВОСТИ Меры центральной тенденции отражают уровень выраженности измеренного признака. Однако не менее важной характеристикой является выраженность индивидуальных различий испытуемых по измеренному признаку. Меры изменчивости {Dispersion) применяются в психологии для численного выражения величины межиндивидуальной вариации признака. Наиболее простой и очевидной мерой изменчивости является размах, указывающий на диапазон изменчивости значений. Размах (Range) — это просто разность максимального и минимального значений: R = x max – x min Ясно, что это очень неустойчивая мера изменчивости, на которую влияют любые возможные «выбросы». Более устойчивыми являются разновидности размаха: размах от 10 до 90-го процентиля (Р90 — Р10) или междуквартильный размах (Р75 - Р25). Последние две меры изменчивости находят свое применение для описания вариации в порядковых данных. А для метрических данных используется дисперсия — величина, название которой в науке является синонимом изменчивости. Дисперсия (Variance) — мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего:
Чем больше изменчивость в данных, тем больше отклонения значений от среднего, тем больше величина дисперсии. Величина дисперсии получается при усреднении всех квадратов отклонений:
Следует отличать теоретическую (генеральную) дисперсию — меру изменчивости бесконечного числа измерений (в генеральной совокупности, популяции в целом) и эмпирическую, или выборочную, дисперсию — для реально измеренного множества значений признака. Выборочное значение в статистике используется для оценки дисперсии в генеральной совокупности. Выше указана формула для генеральной (теоретической) дисперсии (Dx) которая, понятно, не вычисляется. Для вычислений используется формула выборочной (эмпирической) дисперсии (Dx), отличающаяся знаменателем:
ПРИМЕР Вычислим дисперсию признака Х для выборки N = 6
18 0 12 Мх= 18/6 = 3; Dx= 12/(6-1) = 2,4 Стандартное отклонение (Std. deviation) (сигма, среднеквадратическое отклонение) — положительное значение квадратного корня из дисперсии:
На практике чаще используется именно стандартное отклонение, а не дисперсия. Это связано с тем, что сигма выражает изменчивость в исходных единицах измерения признака, а дисперсия — в квадратах исходных единиц. Стандартизация или z-преобразование данных — это перевод измерений в стандартную Z-шкалу (Z-scores) со средним Мz = 0 и Dz (или
В результате преобразованные значения (z-значения) непосредственно выражаются в единицах стандартного отклонения от среднего. Если для одной выборки несколько признаков переведены в z-значения, появляется возможность сравнения уровня выраженности разных признаков у того или иного испытуемого. Для того чтобы избавиться от неизбежных отрицательных и дробных значений, можно перейти к любой другой известной шкале: IQ (среднее 100, сигма 15); Т-оценок (среднее 50, сигма 10); 10-балльной — стенов (среднее 5,5, сигма 2) и др. Перевод в новую шкалу осуществляется путем умножения каждого z-значения на заданную сигму и прибавления среднего:
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 1450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.166.168 (0.008 с.) |

 ПРИМЕР _____________________
ПРИМЕР _____________________

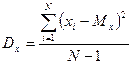

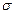 z) = 1. Сначала для переменной, измеренной на выборке, вычисляют среднее Мx стандартное отклонение
z) = 1. Сначала для переменной, измеренной на выборке, вычисляют среднее Мx стандартное отклонение  Затем все значения переменной хi пересчитываются по формуле:
Затем все значения переменной хi пересчитываются по формуле:




