
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод максимального правдоподобия (Д.Лолли).Содержание книги
Поиск на нашем сайте
В отличие от предыдущего, основывается не на предварительной оценке общностей, а на априорном определении числа общих факторов и, в случае большой выборки, позволяет получить статистический критерий значимости полученного факторного решения. Метод минимальных остатков (Г.Харман). Основан на минимизации внедиагональных элементов остаточной корреляционной матрицы; проводится предварительный выбор числа факторов. Альфа-факторный анализ. Был разработан специально для изучения психологических данных; выводы носят, в основном, психометрический, а не статистический характер; минимальное количество общих факторов оценивается по собственным значениям и коэффициентам общности. Факторизация образов, в отличие от классического ФА, предполагает, что общность каждой переменной определяется как линейная регрессия всех остальных переменных.
Перечисленные методы отличаются по способу поиска решения основного уравнения ФА. Выбор метода требует большого опыта работы. Однако некоторые исследователи используют сразу несколько методов, выделенные же во всех методах факторы считают наиболее устойчивыми. Третий этап – это «поворот» факторов в пространстве для достижения простой структуры, в которой каждая переменная характеризуется преобладающим влиянием какого-то одного фактора. Выделяются два класса вращения: ортогональное и косоугольное. К ортогональным методам относятся методы “Varymax” (Kaiser, 1959) – максимизируется разброс квадратов факторных нагрузок по каждому фактору в отдельности, что приводит к увеличению больших нагрузок и уменьшению – маленьких. “Quartymax” – простая структура; в отличие от предыдущего метода формируется для всех факторов одновременно. В некоторых случаях важнее получить простую структуру, чем сохранить ортогональность факторов. Для достижения этого используются аналогичные методы косоугольного поворота: “Oblymin” и “Oblymax”. Конфирматорный факторный анализ. Все описанные выше модели ФА относятся к эксплораторному (поисковому) ФА. Настоящим переворотом в ФА было изобретение конфирматорного (подтверждающего) анализа – КФА. Основной принцип КФА: в качестве гипотезы формируется структура ожидаемой матрицы факторных нагрузок (весов), которая затем накладывается на заданную корреляционную матрицу. Гипотеза подвергается статистической проверке, и постепенно исследователь приходит к соответствующей экспериментальным данным матрице нагрузок, не прибегая к вращению факторов.
Однако гипотеза должна основываться на серьёзном анализе природы изучаемых переменных и лежащих в их основе факторов. Часто для этого проводится предварительный эксплораторный ФА. В качестве математического аппарата в данной модели используется моделирование с помощью линейных структурных уравнений. Данный подход предполагает априорное формулирование гипотез относительно количества латентных и измеряемых переменных, а также их взаимосвязи. Можно выделить следующие этапы: Составляется диаграмма путей, представляющих собой графы, в которых присутствуют измеряемые и латентные переменные, соединённые стрелками (направлены в сторону влияний); Строятся системы уравнений множественной регрессии; их количество соответствует количеству зависимых переменных; Проверяется соответствие предложенной модели (системы уравнений) эмпирическим данным; Осуществляется перебор моделей на данных одной выборки. Метод КФА позволяет оценить валидность тестов (конструктную, дискриминантную, конвергентную). Использование множества индикаторов для каждого латентного конструкта даёт возможность представить степень, с которой каждая переменная объясняет латентную переменную. Остаточная дисперсия обусловлена случайными флуктуациями. С помощью параметров измерительной модели определяется внутренняя согласованность теста, по которой можно говорить об уровне надёжности измерения. В программе LISREL надёжность измеряемых переменных представляется в виде множественных корреляций этих переменных с латентными конструктами (P.Bentler, 1982, 1992; D.Cole, 1987). Моделирование с помощью латентно-структурных уравнений позволяет также проводить анализ данных лонгитюдного исследования с множественными индикаторами (K.Joreskog, 1979, 1988). Модель латентных классов. Все модели латентных структур предполагают локальную независимость характеристик. То есть, для данной латентной характеристики наблюдаемые переменные независимы в смысле теории вероятностей.
В основе модели лежит формула Бэйеса (с учётом экспериментальных данных) их апостериорной плотности распределения. Априорно задаются две латентные характеристики: количество классов (K) и соответствующее им относительное число испытуемых в классе – P(k), а также параметр, позволяющий устанавливать степень вероятности определённого ответа на i -й вопрос при условии, что испытуемый относится к k -му классу – r(k). Априорное задание этих латентных характеристик соответствует гипотезе исследователя, либо задаётся стандартными способами. Вероятность появления i -го профиля
По формуле Бэйеса вычисляется апостериорная (с учётом реальных профилей ответов на вопросы теста) вероятность принадлежности к классу k при условии, что испытуемый имеет i -паттерн ответов:
Для каждого класса строится наиболее вероятный профиль ответов его представителей. Данный метод полезен при адаптации существующих новых опросников и их разработке, а также для анализа результатов исследования. (J.Rost, 1988; Т.Савченко, 1995). При адаптации опросников метод латентно-структурного анализа (LSA) позволяет выделить вопросы теста, которые не соответствуют предложенной модели и подлежат замене или переформулированию. Метод LSA используется также для проведения типологизации по множественному критерию. Модели научения. Вероятностные модели представляют самый широкий класс моделей в психологии. Модели такого типа существуют почти во всех её разделах. Далее будут приведены лишь отдельные, наиболее характерные примеры. Так, в моделях научения есть класс вероятностных моделей. Примером общей вероятностной модели процесса научения является модель, имеющая два подмножества гипотез. (K.Chow, J.Cotton, 1983; Ch.Brainerd, 1982). Согласно этим моделям, испытуемый выдвигает гипотезу из одного подмножества; в случае верного решения в следующем испытании гипотеза выдвигается из этого же множества, а в случае неудачи – с вероятностью p происходит выбор одного из двух подмножеств. Однако модели, имеющие три подмножества гипотез, более адекватно отражают процесс идентификации понятий. В качестве примера адекватной вероятностной модели можно привести разработанную А.Дрынковым (1985) модель, описывающие кривые научения и представляющую собой автомат-подкрепление со счётным множеством расстояний. Модели принятия решения. Теория принятия решений представляет собой набор понятий и семантических методов, позволяющих всесторонне анализировать проблемы принятия решений в условиях неопределённости. Можно выделить три основных подхода к построению моделей процесса принятия решений § теорию статистических решений; § теорию полезности; § теорию игр. Эти теории нашли применение в психологической практике. Теория принятия решений. Теория принятия решений моделирует поведение людей, которые, принимая решения, действуют в соответствии с некоторыми аксиомами. В основе теории принятия решений лежит предположение о том, что выбор альтернатив должен определяться двумя факторами: 1) представлениями лица, принимающего решение о вероятностях различных возможных исходов, которые могут иметь место при выборе того или иного варианта решения; 2) предпочтениями, отдаваемыми различным исходам. Первое – субъективная вероятность, второе – ожидаемая полезность.
Теория полезности. Основы современной теории полезности были заложены А.Крамером и Д.Бернулли (1738), которые предположили, что для многих людей полезность богатства увеличивается с убывающей скоростью по мере его роста. Лишь в 1931г. философ и математик Ф.Рамсей построил систему аксиом для субъективно ожидаемой полезности. Опираясь на его результаты, Л.Сэвидж (1964) ввел строгую систему аксиом для субъективно ожидаемой полезности, которая формируется из аксиом предпочтения. Теория предпочтения основывается на отношении нестрогого В настоящее время модель Севиджа для субъективно ожидаемой полезности получила наибольшее признание среди теорий принятия решений с риском: SEU = P* U, где SEU – субъективно ожидаемая полезность исхода; U –полезность наступившего исхода; P* - субъективная вероятность наступившего исхода. Субъективная вероятность – число, выражающее степень возможности данного события (по мнению субъекта). С.Стивенс и Е.Галантер (1957) получили линейную функцию субъективной вероятности с искажениями на концах шкалы. Позже А.Тверски и Д.Канеман (1974) показали, что люди недооценивают низкие вероятности и переоценивают высокие. В теории максимизации принимаются аксиомы, комбинирующие субъективную вероятность и полезность. В теории принятия решений оценки вероятностей, полученные на основе суждения одного лица, входят в сумму Если необходимо использовать уже имеющиеся данные совместно с экспертными оценками, то теорема Бэйеса даёт возможность уточнить вероятностные оценки с учётом полученной дополнительной информации. Для дискретного случая теорема имеет вид:
где S –данные,
Достаточно широкий диапазон суждений можно выразить посредством функции одного класса. Функции внутри класса можно изменять используя теорему Бэйеса. Существуют четыре важных этапа процесса принятия решений: 1) определение альтернативных способов действия; 2) описание вероятностей возможных исходов; 3) ранжирование предпочтений возможных исходов через их полезность; 4) рациональный синтез информации, полученной на первых трёх этапах. Теория игр. Теория игр является «теорией математических моделей принятия оптимальных решений в условиях конфликта» [2]. Она используется для моделирования поведения в конфликтной ситуации. Под конфликтом понимается явление, применительно к которому можно указать, какие стороны и как в нём участвуют, какие возможны исходы, кто и как в них заинтересован. Понятие игры в теории игр аналогично понятию конфликта в психологии. Понятие оптимальности поведения сторон представляет наиболее важный элемент теоретико-игрового подхода к изучению конфликтов, так как выбор принципа оптимальности фактически равнозначен формализации представлений исследователя о модели принятия решений в подобных ситуациях. Одним из наиболее распространённых является принцип максимально гарантированного результата, заключающийся в том, что сторона принимающая решение, всегда выбирает действие, дающее максимально гарантированный эффект независимо от действий других участников конфликта. Родоначальником теории игр является Джон фон Нейман. В России это – Ю.Гермейер, Г.Поспелов. Теория игр, так же как и теория принятия решений, - самостоятельное направление в исследовании операций; она используется во многих науках в качестве аппарата моделирования и аппарата представления. Различаются игры: § позиционные и в нормальной форме; § антагонистические и с непротивоположными интересами; § двух лиц и n лиц. Игра считается полностью заданной, если известно количество участников, их стратегии и матрицы возможных исходов. В конечной игре существуют гарантированные стратегии, обеспечивающие участнику выигрыш, не меньший, чем гарантированный. Л.Севидж ввёл понятие риска. Он работал с матрицей риска, дополняющей матрицу полезности. Иначе говоря, выбирается действие, приводящее к минимизации максимально возможного риска. Ю.Гермейер ввёл аналогичный критерий для игр с непротивоположными интересами. Модели, разработанные на основе теории игр, дают хороший прогноз, однако при моделировании вводится достаточно много ограничений, а также не учитываются личностные характеристики участников, поэтому, несмотря на усовершенствовании математической теории игр, она обладает существенными ограничениями. В связи с этим, актуальной задачей математической психологии в данном направлении можно считать создание формальных математических моделей поведения человека в зависимости от его субъективного опыта, личностных характеристик и мотивации (Т.Савченко, 1990). Важным приложением аппарата теории игр является его использование в экспериментальной психологии в качестве экспериментальной методики изучения поведения в ситуации с непротивоположными интересами (А.Раппопорт, К.Терхьн, М.Пилмак, А.Лебедев, Т.Савченко).
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.013 с.) |

 .
. .
.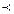 «y не предпочтительнее, чем x» или строгого предпочтения
«y не предпочтительнее, чем x» или строгого предпочтения 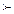 на X, если u(x) > u(y) для любых x и y, таких, что x
на X, если u(x) > u(y) для любых x и y, таких, что x 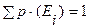 , где Ei (i = 1, 2, …, n) полный набор взаимоисключающих событий, и если она не равна единице, то меняются рассматриваемые оценки [Keeney, 1974]. Для оценки распределения вероятностей величин, имеющих большое количество значений, берётся несколько значений точек функции распределения этой величины, и находится кривая, оптимально проходящая через эти точки.
, где Ei (i = 1, 2, …, n) полный набор взаимоисключающих событий, и если она не равна единице, то меняются рассматриваемые оценки [Keeney, 1974]. Для оценки распределения вероятностей величин, имеющих большое количество значений, берётся несколько значений точек функции распределения этой величины, и находится кривая, оптимально проходящая через эти точки.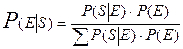 ,
, - вероятность события E при данном S, а
- вероятность события E при данном S, а 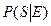 - вероятность S при данном E. Функция
- вероятность S при данном E. Функция 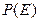 и
и 


