
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многомерное шкалирование (МШ).Содержание книги
Поиск на нашем сайте
Одним из количественных методов изучения психических явлений и процессов, адекватно отражающих их системный характер, признан метод МШ. С его помощью анализируются попарные различия Dij между элементами i и j, в результате чего строится геометрический образ системы. Элементы системы изображаются точками моделирующего пространства, а связям между элементами соответствуют расстояния dij между i и j. Метод МШ разрабатывался в работах У.Торгерсона, Р.Шеппарда, К.Кумбса, Д.Краскала, Ф.Янга, В.Крылова и других. Модели МШ можно расклассифицировать по двум основаниям. По типу данных, полученных в эксперименте: § прямое субъективное шкалирование (задана одна матрица близостей Dij); § модель предпочтений (задана матрица близостей Dij и матрица предпочтений); § модель индивидуального шкалирования (задано несколько матриц близостей). По процедуре реализации метода: § метрическое шкалирование (расстояние в реконструируемом пространстве dij пропорционально различиям Dij, полученным в эксперименте); § неметрическое шкалирование (данные Dij монотонно связаны с расстояниями dij в пространстве Минковского). Метод Шеппарда – Краскала позволяет вычислить показатель стресса, т.е. «невязку» между исходными и вычисленными различиями между объектами:
где dij – расстояние между объектами, вычисленными в процедуре МШ; Dij – исходные различия; § шкалирование в псевдоевклидовом пространстве (не выполняется аксиома неравенства треугольника). В данном случае величина расстояния между объектами определяется по формуле
где § нечёткое шкалирование (данные описаны «нечёткими» психолингвистическими шкалами). Совместное использование МШ и КА позволяет провести анализ данных, более адекватный, чем даёт применение каждого метода в отдельности. При больших выборках необходимо сначала провести КА, а затем, с помощью МШ реконструировать пространство всех классов и каждого класса в отдельности (при необходимости). На основании обобщённого опыта было обнаружено, что при КА маленькие классы адекватны данным, часто являясь осмысленными группами, а большие – нет. И, наоборот, при МШ небольшие изменения в данных могут стать причиной существенных изменений в локальном взаимном расположении точек. В то же время общее расположение точек внутри конфигурации является содержательным (см. работы Граева, Суппеса).
Стохастические модели. Вероятностные модели. Модели с латентными переменными. Модели с латентными переменными являются важным классом вероятностных моделей. Они основаны на предположении о том, что наблюдаемые, объясняемые тестами переменные могут быть объяснены с помощью так называемых латентных более глубинных переменных, которые невозможно измерить непосредственно, однако можно оценить их значение косвенно. К методам латентных переменных относятся: § конфирматорный факторный анализ, § эксплораторный факторный анализ, § регрессионный анализ, § однофакторный анализ, § методы латентных структур. Мак Дональд предложил обобщённую модель латентных структур. Цель создания моделей с латентными переменными – объяснение наблюдаемых переменных и взаимосвязей между ними с помощью латентных переменных. При заданном значении наблюдаемых переменных требуется сконструировать множество латентных переменных и функцию, которая достаточно хорошо аппроксимировала бы наблюдаемые переменные, а в конечном счёте – плотность вероятности наблюдаемой переменной. В факторном анализе основной акцент делается на моделировании значений наблюдаемых переменных, их корреляциях, ковариациях, а в методах латентно-структурного анализа – на моделировании распределения вероятности наблюдаемых переменных. Модели факторного анализа (ФА). Работа Пирсона (1901) – первая, которая была посвящена методу главных компонент. Большой вклад при разработке теста на интеллект внесли К.Спирмен (1926, 1946), Л.Тёрстон (1947, 1951), а при разработке теории личности – Р.Кеттел (1947, 1951) и Г.Ю.Айзенк. Входные данные, обрабатываемые методом ФА, - это корреляционная или ковариационная матрицы. Основная цель – выявление интегральных латентных факторов по наблюдаемым переменным, что означает построение для данной корреляционной матрицы K соответствующей матрицы нагрузок A. Матрица А определяется численными методами, при этом количество факторов не должно превышать количество наблюдаемых переменных. То есть соотношение между n наблюдаемыми переменными должны объясняться возможно меньшим числом латентных факторов.
Первый принцип, лежащий в основе классической модели ФА, - постулат о линейной независимости между линейными характеристиками; Второй – наблюдаемые переменные могут быть представлены как линейная комбинация некоторых латентных факторов. Ряд этих факторов является общим для нескольких переменных, другие – специфические, связанные, в основном, только с одной переменной. В 60-е годы, в связи с быстрым развитием методов ФА, появилось огромное число различных методов. В дальнейшем проявляется тенденция к обобщениям: возникает нелинейный ФА, построение обобщающей модели с латентными переменными, возникновение и развитие конфирматорного ФА. Обобщённая математическая модель ФА в матричном виде – это Основные этапы ФА: 1. сбор эмпирических данных и подготовка корреляционной (ковариационной) матрицы; 2. выделение первоначальных (ортогональных) факторов; 3. вращение факторной структуры и содержательная интерпретация результатов ФА. Второй этап – это прежде всего выбор метода ФА. Назовём наиболее используемые из них в психологии. Метод главных компонент. Его модель имеет вид
где V – матрица собственных векторов, C – диагональная матрица собственных значений. То есть, в данном методе поиск решения идёт в направлении вычисления собственных векторов (факторов), а собственные значения характеризуют дисперсию (разброс) по факторам. Метод главных факторов. Для определения числа факторов используются различные статистические критерии, при помощи которой проверяется гипотеза о незначительности матрицы корреляционных остатков.
|
||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.38 (0.011 с.) |

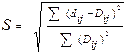 ,
,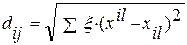
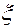 принимает значение (1) для евклидового пространства и (–1) – для псевдоевклидового. Функция стресса для этих пространств вычисляется и выбирается наименьшая;
принимает значение (1) для евклидового пространства и (–1) – для псевдоевклидового. Функция стресса для этих пространств вычисляется и выбирается наименьшая;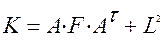 , где A – матрица нагрузок, K – корреляционная матрица, L – матрица ошибок, F – единичная матрица факторов.
, где A – матрица нагрузок, K – корреляционная матрица, L – матрица ошибок, F – единичная матрица факторов.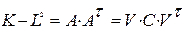 ,
,


