
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная совокупность и выборка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Психология и математика. В настоящее время междисциплинарный подход становится все более привычным в практике подготовки специалистов. Широко он используется и при подготовке психологов. Именно на стыке математических и психологических предметов родилась сравнительно новая дисциплина «Математические методы в психологии». Благодаря проникновению математического аппарата в психологию, последняя смогла выйти за рамки интроспекции и получила возможность количественно описывать и сравнивать наблюдаемые явления. Впоследствии некоторые методы, такие как корреляционный и факторный анализ, появились именно благодаря усилиям психологов. Именно математический аппарат является удобным инструментом описания и моделирования тех или иных явлений в различных отраслях человеческой деятельности. Современному психологу владение математическим статистикой необходимо прежде всего потому, что без нее психолог не сможет обосновать свои рассуждения и будет не в состоянии доказать закономерность своих выводов. Знания этого предмета также необходимы, чтобы быть хорошим психодиагностом, математически правильно понимать и интерпретировать результаты тестирования. Современный этап развития психологической пауки характеризуется экстенсивным развертыванием исследований в различных направлениях, накоплением огромного фактического материала и широким включением этой науки в решение практических задач. Опыт других наук показывает, что на определенных этапах (сходных с тем, который переживает сейчас психология) неизбежно возникают задачи систематизации накапливаемых данных, их обобщения и формализации. Важнейшим (хотя и не единственным) средством решения этих задач является использование математики. Вот почему в последнее время так часто возникают дискуссии о взаимоотношениях психологии и математики, о возможностях применения математических методов для описания и анализа результатов психологических исследований. В этом отношении психология ничем не отличается от других конкретных наук. Вопрос о связи с математикой поставлен в ней так же остро, как в свое время он был поставлен в физике, затем в химии и биологии; как ставится он сейчас в экономике, лингвистике и некоторых других науках.
Психология, которую еще недавно часто относили к ветви чисто гуманитарных наук (рассматривали ее как область философии и педагогики) по методам исследований, принципам их организации, по подходам к анализу получаемых результатов, сейчас вплотную подходит к границам естественных наук. Связанное с этим проникновение в психологические исследования математических методов существенно изменяет их характер. С одной стороны, возникают новые возможности получения и анализа результатов психологического исследования. С другой, предъявляются более строгие требования к понятийному аппарату психологии, к постановке задач исследования и построению новых теорий. Вопрос о применении математических методов в психологии не нов. Еще в середине XIX и начале XX в. наблюдаются, правда, еще не вполне регулярные, но тем не менее приносящие взаимную пользу, - попытки провести аналогии между психологическими и физическими исследованиями, особенно в области построения лабораторного эксперимента, анализа и обработки экспериментальных данных. По существу уже в первых экспериментально-психологических исследованиях (например, в классической психофизике, в работах по изучению сенсомоторных реакций) для обработки получаемых данных и их обобщения был использован существовавший в то время математический аппарат. Почти одновременно в психологию и физику приходят вероятностные и статистические методы, теория дифференциальных уравнений, вариационное исчисление и другие. В психологии работают известные математики и физики - Г. Т. Фехнер, Г. Гельмгольц, В. Вундт, интерес к психологическим исследованиям проявляют А. Пуанкаре, Ж. Адамар, Н. Бор, А. Эйнштейн. О том, чтобы математически описать деятельность мозга, мечтал И. П. Павлов. Исследования того периода можно отнести к числу самых первых пробных шагов на пути применения математических методов в психологических исследованиях. Но идеи того периода оставили в психологии заметный след. Более того, описанные в математической форме результаты ряда исследований вошли в психологическую науку как существенные достижения. Примером тому может служить знаменитый закон Фехнера, характеризующий зависимость интенсивности ощущения от интенсивности стимула (В современной психофизике закон Фехнера подвергается серьезной критике. Однако важно отметить, что эта критика ведется в русле математического подхода к изучению ощущений. Так, С. С. Стивене [75] противопоставляет утверждаемой Фехнером логарифмической зависимости ощущения от стимула степенную; Свете, Таннер и Бердзал [71] подходят к изучению ощущений с позиций статистической теории принятия решения). Он до сих пор приводится во всех учебных пособиях и учебниках по психологии.
Однако на первых этапах развития экспериментальной психологии математические методы использовались для анализа и описания сравнительно простых проявлений психического. С их помощью, например, выявлялась зависимость времени сенсомоторной реакции от интенсивности стимула, измерялась абсолютная и дифференциальная чувствительность различных органов чувств и т. п. Существовавшие в то время математические методы, собственно, и не позволяли исследовать более сложные проявления психического. Вторая четверть XX в. в развитии психологии характеризуется некоторой потерей интереса к математическим методам. В психологических исследованиях преобладают качественные описания, количественному анализу уделяется весьма незначительное внимание, формализация не пользуется популярностью. Интерес к применению математических методов с новой силой вспыхнул в середине XX в. И это в значительной мере стало возможным благодаря развитию самой математики, а также ряда технических наук. В это время зарождаются и развиваются такие дисциплины, как теория информации, теория алгоритмов, появляются методы математического описания процессов поведения, регуляции и организации систем, начинают развиваться кибернетика и теория систем. Вместе с тем существенные изменения происходят и в самой психологии: возникают новые задачи и формируются новые направления исследований. Не рассматривая структуру современной психологии, отметим только, что для многих ее областей характерна большая потребность в использовании математики. Существенную роль в проникновении математики в психологию сыграла (и продолжает играть) инженерная психология. Возникшая как ответ на потребность практики в исследовании систем "человек - машина" (деятельности человека в системах контроля и управления), инженерная психология первой из психологических дисциплин попыталась применить новые математические подходы и методы. Несколько позднее они стали использоваться также и в других областях психологии (социальной, педагогической, медицинской и т. д.). В связи с развитием психологических исследований и все более широким применением в них математики, естественно, возникает задача создания специального метаязыка психологической науки, который мог бы охватить единым терминологическим (и понятийным) аппаратом систему психологических явлений, человеческую деятельность и функционирование сложных систем, включающих человека (типа "человек - машина", "рабочая группа", "коллектив людей - техника"). Вместе с тем применение психологических знаний в практике проектирования сложных систем и необходимость описания этих систем единым языком вызвали дополнительные требования к строгости, точности, качественной и количественной определенности многих как новых, так и старых классических психологических методов, понятий, концепций и теорий.
Не менее мощным стимулом применения математических методов в психологии явилось широкое использование вычислительной техники при изучении явлений, связанных с деятельностью человека. Следует, однако, отметить, что процесс "внедрения" математических методов в психологию идет неравномерно и связан с определенными трудностями. Возникающие в связи с этим процессом проблемы условно можно разделить на следующие группы: 1) методологические проблемы использования математики в психологии; 2) построение психологических шкал и психологические измерения; 3) планирование психологических экспериментов и обработка получаемых данных; 4) использование методов математического моделирования в психологии; 5) информация и психические процессы; 6) математические методы в проектировании деятельности человека; 7) системный анализ в психологии. 8) применение электронно-вычислительной техники в психологии. Разумеется, это разделение может рассматриваться как удобная рабочая схема, ни в коей мере не претендующая на содержательную классификацию проблем (скорее, она констатирует направления, в которых ведутся поиски). По нашему мнению, время для построения такой классификации еще не настало. Сделав эти предварительные замечания, перейдем к рассмотрению отдельных групп проблем.
Измерение. Шкалы измерения. В психологии довольно часто приходится иметь дело с измерением. По сути дела любой психологический тест является инструментом измерения, результатом которого, чаще всего, являются числовые данные. Измерение – операция для определения отношения одного объекта к другому. Измерение реализуется за счет приписывания объектам значений так, чтобы отношения между значениями отражали отношения между объектами. К примеру, мы измеряем рост двух людей (объект измерения - рост). Получив значения 170 и 185 см. мы можем точно сказать, что один человек выше другого. Данный вывод был получен благодаря измерению роста. Таким образом, отношение между объектами было передано с помощью чисел. В психологии можем видеть аналогичные предыдущему примеру явления. Мы используем тесты интеллекта, чтобы получить числовое значение IQ и иметь возможность сравнить его с нормативным значением, используем тесты личности, чтобы на основе полученных чисел описать психологические особенности человека, используем тесты достижений, чтобы выяснить насколько хорошо был усвоен учебный материал. Измерением так же является подсчет количества определённых актов поведения в ходе наблюдения за испытуемыми, подсчет площади штриховки в проективных рисунках, подсчет количества ошибок в корректурной пробе.
В случае с ростом объектом измерения был не человек, а его рост. Изучая психику человека мы так же измеряем не его самого, а определённые психологические особенности: черты личности, интеллект, отдельные характеристики познавательной сферы и т.д. Всё, что мы измеряем называется переменными. Переменная – свойство, которое может менять своё значение. Рост является свойством всех людей, но у каждого он разный, а значит является переменной. Пол так же является переменной, но может принимать всего 2 значения. Все показатели тестов в психологии являются переменными. Результаты некоторых психологических тестов, на первый взгляд, очень трудно представить как результат измерения и трудно понять, какие свойства (переменные) измеряются этими тестами. Яркий пример тому – проективные тесты, особенно рисуночные и вербальные. За каждым элементом рисунка скрывается какая-либо психологическая особенность (переменная) и говоря о выраженности либо невыраженности этой переменной на основе элемента рисунка мы производим акт измерения. Таким образом, несмотря на огромное количество переменных, измеряемых с помощью проективных рисунков измерение чаще всего сводится к простой констатации факта «переменная выражена / не выражена», реже имеется три или больше градации. Гораздо проще обстоит дело с тестами, в которых нужно что-либо упорядочить, т.к. их результат – число, отражающее порядковое место. Ещё более очевидны результаты тестов-опросников, тестов интеллекта и познавательных способностей. Таким образом, тест, как инструмент измерения, накладывает свои ограничения на получаемый результат. Такое ограничение называется шкалой измерения. Шкала измерения – ограничение типа отношений между значениями переменных, накладываемое на результаты измерений. Чаще всего, шкала измерения зависит от инструмента измерения. К примеру, если переменной является цвет глаз, то мы не можем сказать, что один человек больше или меньше другого по этой переменной, мы так же не можем найти среднее арифметическое цвета. Если переменной является порядок (именно порядок) рождения детей в семье, то мы можем сказать, что первый ребенок однозначно старше второго, но не можем сказать на сколько он старше (отношения «больше/меньше»). Имея результаты теста интеллекта, мы можем однозначно сказать на сколько один человек интеллектуальнее другого. С.Стивенс рассматривал четыре шкалы измерения. 1. Шкала наименований - простейшая из шкал измерения. Числа (равно как буквы, слова или любые символы) используются для различения объектов. Отображает те отношения, посредством которых объекты группируются в отдельные непересекающиеся классы. Номер (буква, название) класса не отражает его количественного содержания. Примером шкалы такого рода может служить классификация испытуемых на мужчин и женщин, нумерация игроков спортивных команд, номера телефонов, паспортов, штрих-коды товаров. Все эти переменные не отражают отношений больше/меньше, а значит являются шкалой наименований.
Особым подвидом шкалы наименований является дихотомическая шкала, которая кодируется двумя взаимоисключающими значениями (1/0). Пол человека является типичной дихотомической переменной. В шкале наименований нельзя сказать, что один объект больше или меньше другого, на сколько единиц они различаются и во сколько раз. Возможна лишь операция классификации — отличается/не отличается. В психологии иногда невозможно избежать шкалы наименований, особенно при анализе рисунков. К примеру, рисуя дом, дети часто рисуют солнце в верхней части листа. Можно предположить, что расположение солнца слева, посередине, справа или отсутствие солнца вообще может говорить о некоторых психологических качествах ребенка. Перечисленные варианты расположения солнца являются значениями переменной шкалы наименований. Причем, мы можем обозначить варианты расположения номерами, буквами или оставить их в виде слов, но как бы мы их не называли, мы не можем сказать, что один ребенок «больше» другого, если нарисовал солнце не посередине, а слева. Но мы можем точно сказать, что ребенок, нарисовавший солнце справа однозначно не является тем, кто нарисовал солнце слева (или не входит в группу). Таким образом, шкала наименований отражает отношения типа: похож/не похож, тот/не тот, относится к группе/не относится к группе.
2. Порядковая (ранговая) шкала - отображение отношений порядка. Единственно возможные отношения между объектами измерения в данной шкале – это больше/меньше, лучше/хуже. Самой типичной переменной этой шкалы является место, занятое спортсменом на соревнованиях. Известно, что победители соревнований получают первое, второе и третье место и мы точно знаем, что спортсмен с первым местом имеет лучшие результаты, чем спортсмен со вторым местом. Кроме места, имеем возможность узнать и конкретные результаты спортсмена. В психологии возникают менее определенные ситуации. К примеру, когда человека просят проранжировать цвета по предпочтению, от самого приятного, до самого неприятного. В этом случае, мы точно можем сказать, что один цвет приятнее другого, но о единицах измерения мы не можем даже предположить, т.к. человек ранжировал цвета не на основе каких-либо единиц измерения, а основываясь на собственных чувствах. То же самое происходит в тесте Рокича, по результатам которого мы так же не знаем на сколько единиц одна ценность выше (больше) другой. Т.е., в отличие от соревнований, мы даже не имеем возможности узнать точные баллы различий. Проведя измерение в порядковой шкале нельзя узнать на сколько единиц отличаются объекты, тем более во сколько раз они отличаются.
3. Интервальная шкала - помимо отношений указанных для шкал наименования и порядка, отображает отношение расстояния (разности) между объектами. Разности между соседними точками в этой шкале равны. Большинство психологических тестов содержат нормы, которые и являются образцом интервальной шкалы. Коэфициент интеллекта, результаты теста FPI, шкала градусов цельсия – всё это интервальные шкалы. Ноль в них условный: для IQ и FPI ноль – это минимально возможный балл теста (очевидно, что даже проставленные наугад ответы в тесте интеллекта, позволят получить какой-либо балл отличный от нуля). Если бы мы не создавали условный ноль в шкале, а использовали реальный ноль как начало отсчета, то получили бы шкалу отношений, но мы знаем, что интеллект не может быть нулевым. Не психологический пример шкалы интервалов — шкала градусов Цельсия. Ноль здесь условный — температура замерзания воды и существует единица измерения — градус Цельсия. Хотя мы знаем, что существует абсолютный температурный ноль - это минимальный предел температуры, которую может иметь физическое тело, который в шкале Цельсия равен -273,15 градуса. Таким образом, условный ноль и наличие равных интервалов между единицами измерения являются главными признаками шкалы интервалов. Измерив явление в интервальной шкале, мы можем сказать, что один объект на определенное количество единиц больше или меньше другого.
4. Шкала отношений. В отличие от шкалы интервалов может отражать то, во сколько один показатель больше другого. Шкала отношений имеет нулевую точку, которая характеризует полное отсутствие измеряемого качества. Данная шкала допускает преобразование подобия (умножение на константу). Определение нулевой точки - сложная задача для психологических исследований, накладывающая ограничение на использование данной шкалы. С помощью таких шкал могут быть измерены масса, длина, сила, стоимость (цена), т.е. всё, что имеет гипотетический абсолютный ноль. Вывод Любое измерение производится с помощью инструмента измерения. То, что измеряется называется переменной, то чем измеряют – инструмент измерения. Результаты измерения называются данными либо результатами (говорят «были получены данные измерения»). Полученные данные могут быть разного качества – относиться к одной из четырех шкал измерения. Каждая шкала ограничивает использование определённых математических операций, и соответственно ограничивает применение определённых методов математической статистики.
Таблицы и графики.
Наиболее распространенной формой группировки экспериментальных данных являются статистические таблицы. Таблицы бывают простыми и сложными. К простым относятся таблицы, применяемые при альтернативной группировке, когда одна группа испытуемых противопоставляется другой; например, здоровые — больным, высокие люди — низким и т.п. Пример простой таблицы приведен ниже (см. Таблицу 3.1). В ней представлены результаты обследования мануальной асимметрии у 110 учащихся 3—6-х классов. Таблица 3.1
Из таблицы видно, что леворукие ученики чаще встречаются среди учащихся пятых и шестых классов, чем среди третьих и четвертых классов. Можно в большей степени детализировать эту таблицу, выделив каждый класс в отдельную строку: Таблица 3.2
Из таблицы 3.2 хорошо видно, что леворуких учащихся больше в пятых классах школы, и меньше — в третьих. Простые таблицы рекомендуется использовать, когда измерение изучаемых признаков производится в номинативной или ранговой шкале. Усложнение таблиц происходит за счет возрастания объема и степени дифференцированности представленной в них информации. К сложным таблицам относят так называемые многопольные таблицы, которые могут использоваться при выяснении причинно-следственных отношений между варьирующими признаками. Такие таблицы, как правило, имеют сложное строение, позволяющее одновременно осуществлять разные варианты группировки данных. Примером сложной таблицы служит Таблица 3.3, в которой представлены классические данные Ф. Гальтона, иллюстрирующие наличие положительной зависимости между ростом родителей и их детей. Таблица организована таким образом, что позволяет оценить частоту встречаемости в популяции однозначно фиксируемых соотношений роста родителей и роста ребенка. Например, при низком росте родителей в 66 дюймов (1 дюйм равен 2,54 см) только один из 144 обследованных детей имел рост в 60,7 дюймов, а 56 детей имели рост 66,7 дюйма. В то же время высокий рост детей (74,7 дюйма) был зафиксирован только в тех семьях, где родители имели рост не ниже 70 дюймов. Таблица 3.3
Эта таблица позволяет выявить тенденцию, заключающуюся в том, что у высоких родителей, как правило, дети имеют высокий рост, а у низкорослых родителей чаще бывают дети невысокого роста. Данный пример показывает, что таблицы имеют не только иллюстративное, но и аналитическое значение, позволяя обнаруживать разные аспекты связей между варьирующими признаками. Следует запомнить, что правильно составленные таблицы — это большое подспорье в экспериментальной работе, позволяющее одновременно осуществлять разные варианты группировки полученных данных. Статистические ряды Особую форму группировки данных представляют так называемые статистические ряды, или числовые значения признака, расположенного в определенном порядке. В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики, регрессии, ряды ранжированных значений признаков и ряды накопленных частот. Наиболее часто в психологии используются вариационные ряды, ряды регрессии и ряды ранжированных значений признаков. Вариационным рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной выборке. Например, психолог провел тестирование интеллекта по тесту Векслера у 25 школьников, и сырые баллы по второму субтесту оказались следующими: 6, 9, 5, 7, 10, 8, 9, 10, 8, 11, 9, 12, 9, 8, 10, 11, 9, 10, 8, 10, 7, 9, 10, 9, 11. Как видим, некоторые цифры попадаются в данном ряду по несколько раз. Следовательно, учитывая число повторений, данные ряд можно представить в более удобной, компактной форме: Варианты х, 6 9 5 7 10 8 11 12 (3.1) Частоты вариант.f117126431 Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами, или весами, вариант. Они обозначаются строчной буквой латинского алфавита.£ и имеют индекс «/», соответствующий номеру переменной в вариационном ряду. Общая сумма частот вариационного ряда равна объему выборки, т.е. л = £f, =1+7+1+2+6+4+3+1 = 25 Частоты можно выражать и в процентах. При этом общая сумма частот или объем выборки принимается за 100%. Процент каждой отдельной частоты или веса подсчитывается по формуле: П1% = f 1 : n х 100% (3.2) Процентное представление частот полезно в тех случаях, когда приходится сравнивать вариационные ряды, сильно различающиеся по объемам. Например, при тестировании школьной готовности детей города, поселка городского типа и села были обследованы выборки детей численностью 1000, 300 и 100 человека соответственно. Различие в объемах выборок очевидно. Поэтому сравнение результатов тестирования лучше проводить, используя проценты частот. Приведенный выше ряд (3.1) можно представить по другому. Если элементы ряда расположить в возрастающем порядке, то получится так называемый ранжированный вариационный ряд: Варианты х, 56789 10 1112 (3.3) Частоты f 112 4 7 6 3 1 Подобная форма представления (3.3) более предпочтительна, чем (3.1), поскольку лучше иллюстрирует закономерность варьирования признака. Частоты, характеризующие ранжированный вариационный ряд, "можно складывать, или накапливать. Накопленные частоты получаются последовательным суммированием значений частот от первой частоты до последней. В качестве примера вновь обратимся к ряду 3.3. Преобразуем его в ряд 3.4 в котором введем дополнительную строчку и назовем ее «кумуляты частот». Варианты х, 5 6 7 8 9 10 11 12 Частоты f. 112 4 7 6 3 1 (3.4) Кумуляты частот 1 2 4 8 15 21 24 25 Рассмотрим подробно как получилась последняя строчка. В начале ряда частот стоит 1. В кумулятивном ряду на втором месте стоит 2 — это сумма первой и второй частоты, т.е. 1 + 1, на третьем месте стоит 4 это сумма второй (уже накопленной частоты) и третьей частоты, т.е. 2 + 2, на четвертом 8 = 4 + 4 и т.д. МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ Мера центральной тенденции (Central Tendency) — ^то число, характеризующее выборку по уровню выраженности измеренного признака. ч Существуют три способа определения «центральной тенденции», каждому из которых соответствует своя мера: мода, медиана и выборочное среднее. Мода (Mode) — это такое значение из множества измерений, которое встречается наиболее часто. Моде, или модальному интервалу признака, соответствует наибольший подъем (вершина) графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение Называется унимодальным. П РИМЕР _____________ Среди 8 значений признака (3, 7, 3, 5, 7, 8, 7, 6) мода Мо = 7 как наиболее часто встречающееся значение. В табл. 3.2 предыдущего параграфа Мо = 3, а в табл. 3.3 модальным является интервал 50-54. Когда два соседних значения встречаются одинаково часто и чаще, чем любое другое значение, мода есть среднее этих двух значений. Распределение может иметь и не одну моду. Когда все значения встречаются одинаково часто, принято считать, что такое распределение не имеет моды. Бимодальное распределение имеет на графике распределения две вершины, даже если частоты для двух вершин не строго равны. В последнем случае выделяют большую и меньшую моду. Во всей группе может быть и несколько локальных вершин распределения частот. Тогда выделяют наибольшую моду и локальные моды. Еще раз отметим, что мода — это значение признака, а не его частота. Медиана (Median) — это такое значение признака, которое делит упорядоченное (ранжированное) множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая — больше. Таким образом, первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом: · если данные содержат нечетное число значений (8, 9, 10, 13, 15), то медиана есть центральное значение, т. е. Md= 10; · если данные содержат четное число значений (5, 8, 9, 11), то медиана есть точка, лежащая посередине между двумя центральными значениями, т. е. Md =(8+9)/2 = 8,5. Среднее (Mean) (Мх — выборочное среднее, среднее арифметическое) — определяется как сумма всех значений измеренного признаку, деленная на 1 количество суммированных значений. Если некоторый признак X измерен в группе испытуемых численностью N, мы получим значения: х1, х2,..., xi..., хn (где i — текущий номер испытуемого, от 1 до N). Тогда среднее значение Мx определяется по формуле:
КВАНТИЛИ РАСПРЕДЕЛЕНИЯ Помимо мер центральной тенденции в психологии широко используются меры положения, которые называются квантилями распределения. Квантиль — это точка на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на две группы с известным соотношением их численности. С одним из квантилей мы уже знакомы — это медиана. Это значение признака, которое делит всю совокупность измерений на две группы с равной численностью. Кроме медианы часто используются процентили и квартили. Процентили {Percentiles) — это 99 точек — значений признака (Р1..., Р99), которые делят упорядоченное (по возрастанию) множество наблюдений на 100 частей, равных по численности. Определение конкретного значения про-центиля аналогично определению медианы. Например, при определении 10-го процентиля, Р10, сначала все значения признака упорядочиваются по возрастанию. Затем отсчитывается 10% испытуемых, имеющих наименьшую выраженность признака. Р10будет соответствовать тому значению признака, который отделяет эти 10% испытуемых от остальных 90%. Квартили (Quartlles) — это 3 точки — значения признака (Р2$, JPso» Лз)> которые делят упорядоченное (по возрастанию) множество наблюдений на 4 равные по численности части. Первый квартиль соответствует 25-му процентилю, второй — 50-му процентилю или медиане, третий квартиль соответствует 75-му процентилю. Процентили и квартили используются для определения частоты встречаемости тех или иных значений (или интервалов) измеренного признака или для выделения подгрупп и отдельных испытуемых, наиболее типичных или нетипичных для данного множества наблюдений. МЕРЫ ИЗМЕНЧИВОСТИ Меры центральной тенденции отражают уровень выраженности измеренного признака. Однако не менее важной характеристикой является выраженность индивидуальных различий испытуемых по измеренному признаку. Меры изменчивости {Dispersion) применяются в психологии для численного выражения величины межиндивидуальной вариации признака. Наиболее простой и очевидной мерой изменчивости является размах, указывающий на диапазон изменчивости значений. Размах (Range) — это просто разность максимального и минимального значений: R = x max – x min Ясно, что это очень неустойчивая мера изменчивости, на которую влияют любые возможные «выбросы». Более устойчивыми являются разновидности размаха: размах от 10 до 90-го процентиля (Р90 — Р10) или междуквартильный размах (Р75 - Р25). Последние две меры изменчивости находят свое применение для описания вариации в порядковых данных. А для метрических данных используется дисперсия — величина, название которой в науке является синонимом изменчивости. Дисперсия (Variance) — мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего:
Чем больше изменчивость в данных, тем больше отклонения значений от среднего, тем больше величина дисперсии. Величина дисперсии получается при усреднении всех квадратов отклонений:
Следует отличать теоретическую (генеральную) дисперсию — меру изменчивости бесконечного числа измерений (в генеральной совокупности, популяции в целом) и эмпирическую, или выборочную, дисперсию — для реально измеренного множества значений признака. Выборочное значение в статистике используется для оценки дисперсии в генеральной совокупности. Выше указана формула для генеральной (теоретической) дисперсии (Dx) которая, понятно, не вычисляется. Для вычислений используется формула выборочной (эмпирической) дисперсии (Dx), отличающаяся знаменателем:
ПРИМЕР Вычислим дисперсию признака Х для выборки N = 6
18 0 12 Мх= 18/6 = 3; Dx= 12/(6-1) = 2,4 Стандартное отклонение (Std. deviation) (сигма, среднеквадратическое отклонение) — положительное значение квадратного корня из дисперсии:
На практике чаще используется именно стандартное отклонение, а не дисперсия. Это связано с тем, что сигма выражает изменчивость в исходных единицах измерения признака, а дисперсия — в квадратах исходных единиц. Стандартизация или z-преобразование данных — это перевод измерений в стандартную Z-шкалу (Z-scores) со средним Мz = 0 и Dz (или
В результате преобразованные значения (z-значения) непосредственно выражаются в единицах стандартного отклонения от среднего. Если для одной выборки несколько признаков переведены в z-значения, появляется возможность сравнения уровня выраженности разных признаков у того или иного испытуемого. Для того чтобы избавиться от неизбежных отрицательных и дробных значений, можно перейти к любой другой известной шкале: IQ (среднее 100, сигма 15); Т-оценок (среднее 50, сигма 10); 10-балльной — стенов (среднее 5,5, сигма 2) и др. Перевод в новую шкалу осуществляется путем умножения каждого z-значения на заданную сигму и прибавления среднего:
Критерий Стьюдента t-критерий Стьюдента применяется, когда необходимо сделать статистический вывод, равно ли математическое ожидание M{ Х} генеральной совокупности некоторому предполагаемому значению С или когда требуется построить доверительный интервал для M{ Х}. Обнаружено, что случайная величина t (при независимых наблюдениях) распределена по закону Стьюдента, если Х распределена нормально:
где N- общее число наблюдений (объем выборки), Х - среднее арифметическое случайной переменной Х; S{Х), S{X}- среднеквадратическое отклонение соответственно единичных значений Х и среднего арифметического Х. На рис.1.2 показаны кривы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.21.176 (0.015 с.) |

 (4.1)
(4.1)

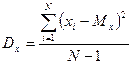

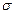 z) = 1. Сначала для переменной, измеренной на выборке, вычисляют среднее Мx стандартное отклонение
z) = 1. Сначала для переменной, измеренной на выборке, вычисляют среднее Мx стандартное отклонение  Затем все значения переменной хi пересчитываются по формуле:
Затем все значения переменной хi пересчитываются по формуле:





