
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели теории графов и геометрическое моделирование.Содержание книги
Поиск на нашем сайте
К данному типу относится моделирование психологических структур и процессов. Например, восприятие можно моделировать с помощью субъективных пространств; при разработке теории личности используются модели классификации и реконструируются семантические пространства и т.д. эти модели строятся на основе применения методов многомерного шкалирования и кластерного анализа. Входными данными в эти методы являются матрицы близостей. Для подсчёта матрицы расстояния необходимо выбрать метрику или метод вычисления расстояния между объектами в многомерном пространстве. Наиболее часто используются следующие метрики: Евклида:
сити-блок (Манхеттен):
Минковского:
метрика на основе корреляции Пирсона:
метрика на основе корреляции Спирмена:
i,j – номера столбцов; k – номер строки; dij – элемент матрицы расстояний; xik, xjk – элемент исходной матрицы; n –количество объектов. Коэффициент корреляции Пирсона подсчитывается для данных, измеренных в порядковых шкалах и шкалах наименований:
Коэффициент ранговой корреляции rs Спирмена является непараметрическим аналогом классического выборочного коэффициента корреляции (неранговые выборки автоматически ранжируются):
Исходный этап для применения многомерного шкалирования (далее – МШ) и кластерного анализа (КА) – это вычисление расстояний между строками или столбцами. Наиболее распространённой считается обычная евклидова метрика. Её обобщение – метрика Минковского, частным случаем которой является манхэттеновская метрика, или метрика сити-блок. Нормализованные евклидовы расстояния в большей степени подходят для переменных, измеренных в различных единицах или значительно отличающихся по величине. Манхэттеновская метрика, как правило, применяется для номинальных или качественных переменных. Расстояния, вычисляемые на основе коэффициента корреляции, отражают согласованность колебаний оценок, в отличие от метрики Евклида, которая определяет, в среднем, сходные показатели. Кластерный анализ (КА). КА позволяет строить систему классификации исследованных объектов и переменных в виде «дерева» (дендрограммы) или же осуществлять разбиение объектов на заданное число удалённых друг от друга классов.
Методы КА можно расклассифицировать на: Внутренние – признаки классификации равнозначны; Внутренние можно разделить на: Иерархические – процедура классификации имеет древовидную структуру. Иерархические, в свою очередь подразделяются на: Агломеративные – объединяющие; Дивизитивные – разъединяющие. Неиерархические Внешние – существует один главный признак классификации, который определяют по остальным. В психологии наиболее распространён иерархический дивизитивный метод. Он позволяет строить «дерево» классификации n объектов посредством их иерархического объединения в группы или кластеры на основе заданного критерия – минимума расстояния в пространстве m переменных, описывающих объекты. Кроме того, с его помощью осуществляется разбиение некоторого множества объектов на естественное число кластеров. Графическое представление результатов даётся в виде «дерева» иерархической кластеризации. По оси X – объекты, подлежащие классификации (на одинаковом расстоянии друг от друга). По оси Y – расстояния, на которых происходит объединение объектов в кластеры. Для определения естественного числа кластеров вводится оценка разбиения на классы, которую вычисляют по величине отношения средних внутрикластерных расстояний к межкластерным (А.Дрынков, Т.Савченко, 1980). Глобальный минимум оценки характеризует естественное число классов, а локальные - под- и надструктуры. Методы иерархического КА различаются по стратегии объединения, т.е. пересчёта расстояний. Выделяются стратегии ближайшего соседа. При объединении i-го и j-го классов в класс k расстояние между новым классом k и любым другим классом h пересчитываются следующим образом:
Расстояния между другими классами остаются неизменными. Стратегия дальнего соседа:
Группового среднего:
где ni, nj, nk – число объектов в классах i, j, k. Первые две стратегии, за исключением последней, изменяют пространство (сужают и растягивают). Поэтому, если не удаётся если не удаётся получить хорошего разбиения на классы с помощью третьей стратегии (а их необходимо выделить), то используются первые две. При этом первая стратегия объединяет классы по близким границам, а вторая – по дальним.
В социальной психологии при исследовании взаимоотношений в коллективах, помимо разбиения на классы, необходимо установить также объекты, через которые классы связаны друг с другом. На эти вопросы можно ответить с помощью дендритного КА, который часто применяется совместно с иерархическим (Плюта, 1981). Главная роль в нём принадлежит дендриту – ломаной линии, которая не содержит замкнутых ломанных и в то же время соединяет любые два элемента. Предлагается построение дендрита, у которого сумма длин связей минимальна. Сначала к каждому объекту находится ближайший, при этом образуется скопление первого порядка, которые затем также объединяются по величине минимального расстояния до тех пор, пока не будет построен дендрит. Группы объектов считаются вполне отделимыми, если длина дуги между ними Дендриты могут иметь форму розетки, амёбообразного следа, цепочки. При совместном использовании иерархического КА и дендрита распределение элементов по классам осуществляется по первому методу, а взаимосвязи между ними анализируются с помощью дендрита.
|
||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.70.28 (0.007 с.) |

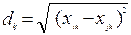

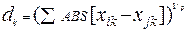
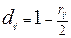


 *
*


 , где
, где  ; Cср - средняя длина дуги; S - стандартное отклонение.
; Cср - средняя длина дуги; S - стандартное отклонение.


