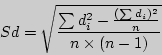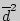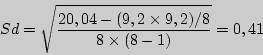Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрические и непараметрические методыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Методы обучения, т.е. нахождения достаточно хорошей распознающей функ- ции f 2 F, традиционно подразделяются на параметрические и непарамет- рические в соответствии с тем, просто или сложно устроено пространство F. Параметрические — это те методы, в которых F = fF(w; ¢)jw 2 Wg для неко- торого достаточно удобного (например, евклидова) пространства параметров W и некоторой функции F: W £ X! Y, а непараметрические — это мето- ды, в которых, якобы, пространство F не зафиксировано заранее, а зависит от обучающего набора T. На самом деле разница между параметрическими и непараметрическими методами — только в употребляемых словах. Полезный пример параметрических методов — методы обучения линейных распознавателей, которых даже для простейшей линейной регрессии (X = Rd, Y = R, W = R £ Rd, F(w; x) = w0 +Pdj=1 wjxj) довольно много. Подробнее эти методы рассматриваются в разделе 2. [А.Б. Мерков] непараметрические методы в математической статистике, методы непосредственной оценки теоретического распределения вероятностей и тех или иных его общих свойств (симметрии и т.п.) по результатам наблюдений. Название Н. м. подчёркивает их отличие от классических (параметрических) методов, в которых предполагается, что неизвестное теоретическое распределение принадлежит какому-либо семейству, зависящему от конечного числа параметров (например, семейству нормальных распределений, и которые позволяют по результатам наблюдений оценивать неизвестные значения этих параметров и проверять те или иные гипотезы относительно их значений. Разработка Н. м. является в значительной степени заслугой советских учёных. Мощность критериев Мощность критерия - это его способность выявлять различия, если они есть. Иными словами, это его способность отклонить нулевую гипотезу об отсутствии различий, если она неверна. Ошибка, состоящая в том, что мы приняли нулевую гипотезу, в то время как она неверна, называется ошибкой II рода. Вероятность такой ошибки обозначается как β. Мощность критерия - это его способность не допустить ошибку II рода, поэтому: Мощность=1—β Мощность критерия определяется эмпирическим путем. Одни и те же задачи могут быть решены с помощью разных критериев, при этом обнаруживается, что некоторые критерии позволяют выявить различия там, где другие оказываются неспособными это сделать, или выявляют более высокий уровень значимости различий. Возникает вопрос: а зачем же тогда использовать менее мощные критерии? Дело в том, что основанием для выбора критерия может быть не только мощность, но и другие его характеристики, а именно: а) простота; б) более широкий диапазон использования (например, по отношению к данным, определенным по номинативной шкале, или по отношению к большим n); в) применимость по отношению к неравным по объему выборкам; г) большая информативность результатов.
БИЛЕТ 10 Классификация задач и методов их решения Множество задач психологического исследования предполагает те или иные сопоставления. Мы сопоставляем группы испытуемых по какому-либо признаку, чтобы выявить различия между ними по этому признаку. Мы сопоставляем то, что было "до" с тем, что стало "после" наших экспериментальных или любых иных воздействий, чтобы определить эффективность этих воздействий. Мы сопоставляем эмпирическое распределение значений признака с каким-либо теоретическим законом распределения или два эмпирических распределения между собой, с тем, чтобы доказать неслучайность выбора альтернатив или различия в форме распределений. Мы, далее, можем сопоставлять два признака, измеренные на одной и той же выборке испытуемых, для того, чтобы установить степень согласованности их изменений, их сопряженность, корреляцию между ними. Наконец, мы можем сопоставлять индивидуальные значения, полученные при разных комбинациях каких-либо существенных условий, с тем чтобы выявить характер взаимодействия этих условий в их влиянии на индивидуальные значения признака. Именно эти задачи позволяет решить тот набор методов, который предлагается настоящим руководством. Все эти методы могут быть использованы при так называемой "ручной" обработке данных. Краткая классификация задач и методов дана в Таблице 1.2. Таблица 1.2 Классификация задач и методов их решения
Сидоренко е.в.
Билет 11 Параметрический критерий различий и сдвигов: Т - Критерий Стьюдента Критерии носят название `` параметрические '', потому, что в формулу их расчета включаются такие параметры выборки, как среднее, дисперсия и др. Как правило, в психологических исследованиях чаще всего применяются два параметрических критерия - это t - критерий Стьюдента, который оценивает различия средних для двух выборок и F - критерий Фишера, оценивающий различия между двумя дисперсиями. Т - Критерий Стьюдента Критерий t Стьюдента направлен на оценку различий величин средних Случай несвязных выборок В общем случае формула для расчета по t - критерию Стьюдента такова:
где Рассмотрим сначала равночисленные выборки. В этом случае n1 = n2 = n, тогда выражение (9.2) будет вычисляться следующим образом:
В случае неравночисленных выборок
В обоих случаях подсчет числа степеней свободы осуществляется по формуле:
где n1 и n2 соответственно величины первой и второй выборки. Понятно, что при численном равенстве выборок k = 2 Это пример, его учить не нужно, но чтоб разобраться, можно посмотреть (Лена) Рассмотрим пример использования t - критерия Стьюдента для несвязных и неравных по численности выборок. Пример: Психолог измерял время сложной сенсомоторной реакции выбора (в мс) в контрольной и экспериментальной группах. В экспериментальную группу (X) входили 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, активно не занимающихся спортом. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом. Результаты эксперимента представим в виде табл. 9, в которой произведем ряд необходимых расчетов: Таблица 9
Средние арифметические составляют в экспериментальной группе Разница по абсолютной величине между средними
Подсчет выражения дает:
Тогда значение
Число степеней свободы 2,13 для P 2,95 для P 4,07 для P Строим ``ось значимости'': Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,]% уровне, или, иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, активно не занимающихся спортом. В терминах статистических гипотез это утверждение звучит так: гипотеза Случай связных выборок В случае связных выборок с равным числом измерений в каждой можно использовать более простую формулу t - критерия Стьюдента. Вычисления значений
где В свою очередь
Число степеней свободы k определяется по формуле k = n - 1 Рассмотрим пример использования t - критерия Стьюдента для связных и, очевидно, равных по численности выборок. Пример: Психолог предположил, что в результате научения время решения эквивалентных задач ``игры в 5'' (т. е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач. Решение задачи представим в виде табл. 10. Таблица 10
Вначале произведем расчет по формуле:
Затем применим формулу:
И, наконец, следует применить формулу. Получим:
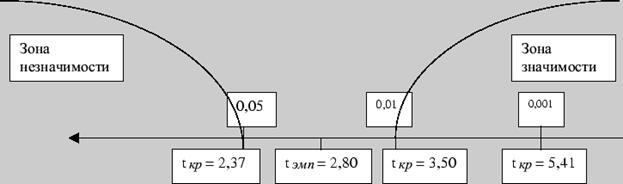
Число степеней свободы: k = 8 - 1 = 7 и по табл. 17 приложения 6 находим 2,37 для P З,50 для P 5,41 для P Строим ось значимости:
Таким образом, на 5% уровне значимости первоначальное предположение подтвердилось, действительно, среднее время решения третьей задачи существенно меньше среднего времени решения первой задачи. В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза Для применения t - критерия Стьюдента необходимо соблюдать следующие условия: Измерение может быть проведено в шкале интервалов и отношений. Сравниваемые выборки должны быть распределены по нормальному закону.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 1287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.240 (0.008 с.) |

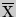 и
и 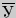 двух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.
двух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.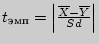

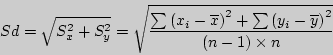
 , выражение будет вычисляться следующим образом:
, выражение будет вычисляться следующим образом:
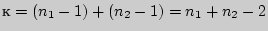
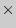 n - 2.
n - 2.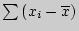
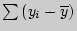
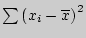
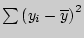
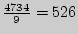 , в контрольной группе
, в контрольной группе 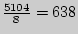

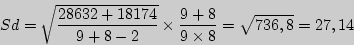
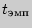 , вычисляемое по формуле (9.1), таково:
, вычисляемое по формуле (9.1), таково: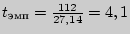
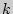 = 9 + 8-2= 15. По табл. 17 приложения 6 для данного числа степеней свободы находим
= 9 + 8-2= 15. По табл. 17 приложения 6 для данного числа степеней свободы находим  :
: 0,05
0,05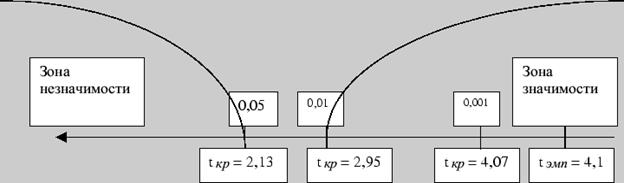
 о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза
о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза 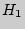 - о различии между экспериментальной и контрольными группами.
- о различии между экспериментальной и контрольными группами.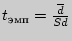

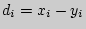 - разности между соответствующими значениями переменной X и переменной Y, а
- разности между соответствующими значениями переменной X и переменной Y, а 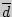 среднее этих разностей.
среднее этих разностей.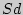 вычисляется по следующей формуле:
вычисляется по следующей формуле: