
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические гипотезы и критерии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(из учебника Мат.стат.) На разных этапах статистического исследования возникает необходимость в формулировании и экспериментальной проверке некоторых предположительных утверждений (гипотез). Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Выдвигается основная (нулевая) гипотеза В результате статистической проверки гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; вероятность совершить такую ошибку обозначают Процедура обоснованного сопоставления высказанной гипотезы с имеющейся выборкой осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотез. Под критической областью понимают совокупность значений критерия, при которых нулевую гипотезу Статистические критерии проверки гипотез разнообразны, но у них единая логическая схема построения, которую представим на рис. 103.
Рис. 103 1. Сравнение двух дисперсий нормальных генеральных совокупностей. При заданном уровне значимости
В качестве критерия проверки нулевой гипотезы принимают случайную величину отношения большей исправленной дисперсии к меньшей
Величина Пример 181. Исследование длительности оборотных средств двух групп предприятий (по 13 предприятий в каждой) дало следующие результаты:
Можно ли считать, что отклонения в длительности оборота оборотных средств групп предприятий одинаковы для уровня значимости 0,1? Решение. В этой задаче надо проверить нулевую гипотезу
По таблице приложения 6 по уровню значимости для двусторонней критической области
Так как Пример 182. Школьникам давались обычные арифметические задачи, а потом одной случайно выбранной половине учащихся сообщалось, что они не выдержали испытания, а остальным - обратное. Затем у каждого из них спрашивали, сколько секунд ему потребуется для решения новой задачи. Экспериментатор, вычисляя разность между определенным временем решения задачи, которое называл школьник, и результатами ранее выполненного задания, получил следующие данные:
Проверьте на уровне значимости 0,01 гипотезу о том, что дисперсия совокупности детских оценок, имеющих отношение к оценке их возможностей, не зависит от того, что сообщалось детям о плохих результатах испытаний или об удачном решении первой задачи. Решение. Применим критерий Фишера-Снедекора для нулевой гипотезы
Критическую точку находим в приложении для уровня значимости
Получили, что 2. Сравнение двух средних нормальных генеральных совокупностей с известными дисперсиями. Проверяется нулевая гипотеза о равенстве генеральных средних рассматриваемых совокупностей с заданными или вычисляемыми дисперсиями. В качестве критерия проверки нулевой гипотезы примем случайную величину
Пример 183. Производительность двух моторных заводов, выпускающих дизельные двигатели, характеризуется следующими данными:
Можно ли считать одинаковыми производительности дизельных двигателей на обоих заводах при уровне значимости Решение. Найдем выборочные числовые характеристики данных независимых выборок:
Найдем наблюдаемое значение критерия:
По условию, конкурирующая гипотеза имеет вид Найдем критическую точку:
по таблице функции Лапласа (прил. 2) находим Так как 3. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности. По выборочной средней при заданном уровне значимости проверяется нулевая гипотеза
которая распределена нормально. Пример 184. Из нормальной генеральной совокупности с известным средним квадратическим отклонением Решение. Найдем наблюдаемое значение критерия:
Найдем критическую точку двусторонней критической области:
и по таблице функции Лапласа находим Поскольку 4. Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события. При заданном уровне значимости В качестве критерия проверки нулевой гипотезы принимаем случайную величину
Пример 185. По 100 независимым испытаниям найдена относительная частота 0,07. При уровне значимости 0,05 проверить нулевую гипотезу Решение. Найдем наблюдаемое значение критерия:
Учитывая, что критическая область двусторонняя, находим
По таблице функции Лапласа (прил. 2) находим Поскольку Критерий Стьюдента t-критерий Стьюдента применяется, когда необходимо сделать статистический вывод, равно ли математическое ожидание M{ Х} генеральной совокупности некоторому предполагаемому значению С или когда требуется построить доверительный интервал для M{ Х}. Обнаружено, что случайная величина t (при независимых наблюдениях) распределена по закону Стьюдента, если Х распределена нормально:
где N- общее число наблюдений (объем выборки), Х - среднее арифметическое случайной переменной Х; S{Х), S{X}- среднеквадратическое отклонение соответственно единичных значений Х и среднего арифметического Х. На рис.1.2 показаны кривые дифференциального закона распределения Ф(t) для различных степеней свободы f=N-1, по которым вычисляют несмещенную оценку дисперсии S2{ Х }. При сравнительно небольших N кривая Ф(t) более пологая, чем нормальный закон распределения Ф(Х). При N----- кривая Ф(t) приближается к кривой нормированного нормального распределения. Из рис.1.2 видно, что t-распределение симметрично относительно t=0, поэтому в таблицах, где даны критические значения t кр = tq,f для принятого уровня значимости q и имеющегося числа степеней свободы f, задаются только положительные tкр. Если при расчете t по формуле (1.3) при подстановке в нее вместо М{X} предполагаемого значения С окажется, что t < tкр, то можно сделать вывод о том, что гипотеза М{X} = С не противоречит результатам наблюдения при принятой уровне значимости q.
В противном случае эта гипотеза отвергается с тем же уровнем значимости q. При этом остается возможность совершить ошибку первого рода, т.е. отвергнуть верную гипотезу с вероятностью q. - Рассмотрим использование t-критерия Стьюдента для построения доверительного интервала для математического ожидания. При t=t кр разность [X - M{Х}] в (1.3) равна половине ширины доверительного интервала __ т.е.
Доверительный интервал, в котором с доверительной вероятностью P=I-q находится математическое ожидание M{X}, определяется следующими выражениями:
Поскольку математическое ожидание М{X} есть истинное, объективно существующее неслучайное значение, а границы интервала - случайные величины (за счет наличия в них случайных величин X и S{X}), то правильно будет говорить о том, что доверительный интервал (1.5), (1.6) с вероятностью Р = I - q накрывает М {X}.
Критерий Фишера Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей, распределенных по нормальному закону. F-критерий Фишера называют дисперсионным отношением, так как он формируется как отношение двух сравниваемых несмещенных оценок дисперсий: причем в числителе ставится большая из двух дисперсий. Расчетное F сравнивают с _____________, которое находятиз таблиц, для степеней свободы _____________________________________где N 1 - число элементов выборки, по который вычислена _______. N 2 - число элементов выборки, по которым получена оценка дисперсии ________. Если F<Fкр, то принимается нулевая гипотеза о равенстве генеральных дисперсий _________________ при принятом уровне значимости q. На рис. 1.3 показаны кривые распределения _____. Зачернена область критических значений F. На практике задача сравнения дисперсий возникает, если требуется сравнить.точность приборов, инструментовили методов измерений. Предпочтительнее тот прибор, инструмент или метод, который обеспечивает наименьшее рассеяние результатов измерений, т.е. наименьшую дисперсию.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.169 (0.008 с.) |

 и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу
и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу  , которая противоречит нулевой.
, которая противоречит нулевой. и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают
и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают  , а мощностью критерия является вероятность
, а мощностью критерия является вероятность  .
.
 проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:
проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

 имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы
имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы  и
и  .
. дня,
дня,  дней,
дней,  дня,
дня,  дней.
дней. о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе
о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе  . Используем критерий Фишера-Снедекора со степенями свободы
. Используем критерий Фишера-Снедекора со степенями свободы  и вычислим наблюдаемое значение критерия (отношение большей дисперсии к меньшей)
и вычислим наблюдаемое значение критерия (отношение большей дисперсии к меньшей)
 и числам степеней свободы
и числам степеней свободы  находим критическую точку
находим критическую точку
 , то нет оснований отвергать нулевую гипотезу о равенстве отклонений в длительности оборота оборотных средств двух групп предприятий.
, то нет оснований отвергать нулевую гипотезу о равенстве отклонений в длительности оборота оборотных средств двух групп предприятий.

 . Вычислим наблюдаемое значение критерия
. Вычислим наблюдаемое значение критерия
 и числам степеней свободы
и числам степеней свободы  и
и  :
:
 и нулевая гипотеза на уровне значимости 0,01 отвергается.
и нулевая гипотеза на уровне значимости 0,01 отвергается.
 ?
?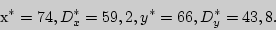

 , поэтому критическая область - двусторонняя.
, поэтому критическая область - двусторонняя.
 .
. , то нулевая гипотеза об одинаковости производительности двух заводов отклоняется.
, то нулевая гипотеза об одинаковости производительности двух заводов отклоняется. о равенстве генеральной средней
о равенстве генеральной средней  гипотетическому значению
гипотетическому значению 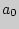 . В качестве проверки нулевой гипотезы примем случайную величину
. В качестве проверки нулевой гипотезы примем случайную величину
 извлечена выборка объема
извлечена выборка объема  и по ней найдена выборочная средняя
и по ней найдена выборочная средняя  . Проверить нулевую гипотезу
. Проверить нулевую гипотезу  , при конкурирующей гипотезе
, при конкурирующей гипотезе  и уровне значимости 0,1.
и уровне значимости 0,1.

 .
. , то нулевая гипотеза принимается.
, то нулевая гипотеза принимается. появления события равна гипотетической вероятности
появления события равна гипотетической вероятности  серии повторных независимых испытаний.
серии повторных независимых испытаний.
 при конкурирующей гипотезе
при конкурирующей гипотезе  .
.
 из равенства
из равенства
 .
. , то нет оснований отвергать гипотезу о незначительном отличии наблюдаемой относительной частоты от гипотетической вероятности.
, то нет оснований отвергать гипотезу о незначительном отличии наблюдаемой относительной частоты от гипотетической вероятности.






