Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение теоретических и эмпирических распределений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В практической работе часто возникает необходимость определить соответствие эмпирического и теоретического распределения или двух и более эмпирических распределений между собой. Общие принципы сравнения основываются на анализе так называемой нулевой гипотезы. Согласно этой гипотезе первоначально принимается, что между эмпирическим и теоретическим распределением признака в генеральной совокупности достоверного различия нет. Статистический анализ должен привести или к отклонению нулевой гипотезы, если доказана достоверность полученных различий, или к ее сохранению, если достоверность различий не доказана, т.е. различия признаны случайными. Отбрасывание нулевой гипотезы должно быть связано с принятием определенного уровня вероятности (значимости). В медико–биологических исследованиях этот уровень должен быть не менее 0,95(a£0,05). Для приближенной проверки гипотезы о нормальном распределении можно воспользоваться показателями асимметрии и эксцесса (формулы 19). Для нормального распределения эти показатели должны быть равны нулю. Однако, часто оценки этих показателей (А и Е), вычисленные для выборок, взятых даже из нормально распределенной совокупности, отличаются от нуля. В этом случае необходимо рассчитать средние квадратические ошибки sА и sЕ по формулам:
где n – объем выборки. Для достаточно большой выборки (n>30), если показатели асимметрии и эксцесса в два и более раза превышают показатели их средних квадратических ошибок, гипотезу о нормальности распределения нужно отвергнуть. Более точную оценку производят, сравнивая теоретические и экспериментальные функции распределения вероятности (накопленные вероятности) по критерию Колмогорова – Смирнова (критерий l, рис.9а) либо функции распределения плотности вероятностей по критерию Пирсона – (критерий c2, рис.9б).
Рис.9. Сравнение теоретических и экспериментальных распределений по: а) критерию Колмогорова – Смирнова, б) критерию Пирсона. Пунктирная линия – эмпирическое распределение, сплошная – теоретическое распределение.
Рассмотрим сравнение теоретического и эмпирического распределений по критерию Пирсона. В этом случае рассчитываются теоретические вероятности (частоты) попадания значений случайной величины в соответствующие интервалы по формуле (17) и таблице 1 Приложения. Критерий c2, предложенный Пирсоном, определяют по формуле:
где mi – экспериментальные частоты попадания значения случайной величины в интервал, npi–теоретические частоты. По таблице 3 Приложения критических точек распределения c2кр по заданному уровню значимости (a) и числу степеней свободы df, находим критическое значение c2кр (a,df). Число степеней свободы – это общее число величин, по которым вычисляются соответствующие статистические показатели, минус число тех условий, которые связывают эти величины, то есть уменьшают возможности вариации между ними. Для определения данного критерия число степеней свободы определяется по следующей формуле: df=k–r–1, где k – число интервалов, r – число параметров предполагаемого распределения. Так как распределение случайной величины, подчиняющейся нормальному закону, можно охарактеризовать двумя параметрами: средней арифметической величиной m и среднеквадратическим отклонением s, то в нашем случае r=2. Число степеней свободы df=k–3, где k – число интервалов группировки. Уровень значимости принимается не более 0,05 (P>95%). Если c2эмп. <c2кр. гипотеза о согласии эмпирического и теоретического распределения не отвергается. Для применения критерия Пирсона необходимо, чтобы количество данных в каждом классе было не менее трех – пяти. Интервалы, в которых это условие не выполняется, следует объединить с соседними. Для закрепления рассмотренного материала, рассмотрим статистическую обработку выборки из 100 значений пульса (ЧСС), измеренного у студентов 1 курса КрасГМА. Наметим основные этапы исследования: 1. Сгруппируем исследуемый ряд по классам. Подсчитаем середины интервалов и частоты попадания в интервал. 2. Построим гистограмму и полигон распределения. 3. Найдем эмпирическую функцию распределения и построим ее график. 4. Вычислим числовые (точечные) характеристики распределения. 5. Найдем интервальные оценки для генеральной средней. Проверим гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону используя критерий Пирсона c2.
При измерении частоты сердечных сокращений у 100 студентов 1–го курса получились следующие величины: 48 56 54 57 47 50 58 59 60 67 68 70 69 74 75 53 58 86 51 88 60 87 65 69 71 68 50 61 49 76 77 61 85 59 88 64 51 86 91 78 52 49 81 55 62 63 73 72 72 66 67 80 79 82 84 75 83 84 83 72 73 73 62 67 81 63 83 64 66 67 67 66 71 68 71 76 63 66 64 66 65 68 76 78 77 68 72 73 74 79 78 77 76 70 71 69 72 73 69 71 Разобьем эти величины на интервалы. Величину интервала найдем из формулы: Dx= h=Dx = Составим таблицу, в которой будут отражены следующие данные: интервалы, середины каждого интервала, частоты попадания в них величин и их относительные частоты. Относительные частоты будут рассчитаны по формуле: т.е. отношение числа величин попавших в интервал к общему количеству величин.
Таблица 4
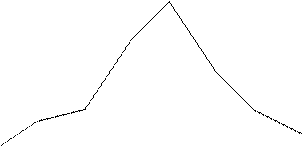
Построим гистограмму и на этом же графике построим полигон.
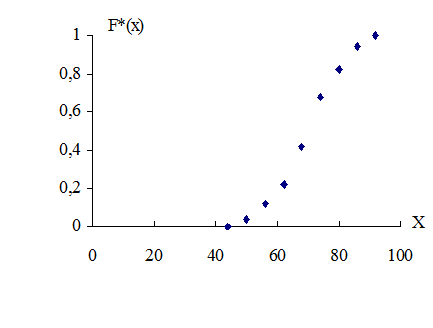
Найдем эмпирическую функцию распределения F*(x). Эта функция определяет для каждого значения х относительную частоту значения Х<х: F*(x)= где nx – число значений меньше х, n – объем выборки. Для построения графика функции F*(x) составим таблицу: Таблица 5
Число значений Х<x получается суммированием всех частот попадания в интервалы меньших значения х из таблицы 4. Например, в интервал меньше значения 56 попадут 8+4=12 вариант. Такой ряд называют рядом накопленных частот.
Построим график эмпирической функции распределения:
0,04 если 44£x<50 0,12 если 50£x<56 0,22 если 56£x<62 F*(x)= 0,42 если 62£x<68 0,68 если 68£x<74 0,82 если 74£x<80 0,94 если 80£x<86 1,00 если 86£x<92 1,00 если x³92
Для вычисления числовых характеристик удобно составить следующую таблицу:
Таблица 6
Найдем выборочную среднюю:
Найдем выборочную дисперсию:
Из нее найдем выборочное среднее квадратическое отклонение:
Найдем коэффициенты асимметрии и эксцесса:
Для предварительного выбора закона распределения вычислим средние квадратические ошибки определения коэффициентов асимметрии и эксцесса.
Одним из признаков распределения случайной величины по нормальному закону является равенство нулю коэффициентов асимметрии и эксцесса. Из приведенных расчетов видно, что выборочные коэффициенты А и Е отличаются от нуля не более, чем на удвоенные средние квадратические ошибки их определения:
что соответствует нормальному закону распределения. Вид полигона и гистограммы относительных частот также напоминает нормальную кривую (кривую Гаусса). Функция плотности вероятности для нормального распределения имеет вид: f(x)= В качестве неизвестных нам параметров mи s возьмем их выборочные оценки
Подставим данные в формулу:
Функция распределения вероятности предполагаемого нормального распределения имеет следующий вид:
По таблице 1 Приложения найдем вероятность того, что значение случайной величины попадет в интервал от а до b: Р(a < x < b)= Гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону, назовем нулевой и проверим ее с помощью критерия согласия Пирсона c2. С этой целью будем сравнивать эмпирические mi (наблюдаемые) и теоретические npi (вычисленные в предположении нормального распределения) частоты. В качестве критерия проверки нулевой гипотезы принимаем случайную величину:
Затем по таблице критических точек распределения c2 (таблица 3 Приложения) по заданному уровню значимости a и числу степеней свободы найдем критическое значение c2кр.(a,df). Если c2эмп.£c2кр.(a,df), то считаем, что данный критерий оснований для отклонения гипотезы не дает, а в противном случае считаем, что гипотеза не согласуется с экспериментальными данными и ее надо отвергнуть. Вычислим вероятности pi: p1=P(44£x<50)= Ф(-1,87283)–Ф(-2,45087)=(1-0,9693)–(1-0,9928)= 0,0307–0,0072=0,0235 p2=P(50 Ф(-1,2948)–Ф(-1,87283)=(1-0,9015)–0,0307= 0,0985–0,0307=0,0678 ... р8 =Р(86 Ф(2,17341)–Ф(1,595376)=0,9861–0,9452=0,0409
Полученные величины сведем в таблицу 7: Таблица 7
c2эмп=4,17. В таблице критических точек распределения c2 по уровню значимости a=0,05 и числу степеней свободы df=k–3=5 найдем:. c2кр.(0,05;5)=11,07. 4,17<11,07 (c2эмп.<c2кр.(0,05;5)). Т.к. c2 наблюдаемое меньше, чем c2 критическое, то нет основания для отклонения гипотезы о нормальном распределении случайной величины. Построим нормальную кривую и сравним ее с полигоном. Сравнение полигона относительных частот и нормальной кривой показывает, что построенная нормальная кривая удовлетворительно сглаживает полигон
Найдем интервальные оценки параметров нормального закона распределения. Для нахождения доверительного интервала, покрывающего математическое ожидание случайной величины, найдем по таблице 2 Приложения по заданной доверительной вероятности p=0,95 (a=0,05) число t=1,96 и при p=0,99 (a=0,01): t=2,58. Вычислим доверительный интервал:
Искомый доверительный интервал для математического ожидания равен:
67,41<m<71,47; 66,8<m<72,1 Выводы: Если будет произведено достаточно большое число выборок случайных величин (измерение частоты пульса ЧСС у студентов КрасГМА), то: 1. При a=0,05. В 95% из них доверительный интервал (67,41; 71,47) покроет математическое ожидание значения ЧСС, и только в 5% случаев математическое ожидание может выйти за границы доверительного интервала. 2. Аналогично при a=0,01. В 99% случаев доверительный интервал (66,8; 72,1) покроет математическое ожидание и в 1% случаев математическое ожидание может выйти за границы доверительного интервала. При анализе распределения первичных данных частоты сердечных сокращений у студентов КрасГМА был установлено, что характер их распределения можно признать нормальным по критерию c2. Среднее значение изученного параметра равно 69,44 уд/мин. Среднеквадратическое отклонение – 10,38; коэффициенты асимметрии и эксцесса – -0,152 и -0,42 соответственно. Выполнено построение эмпирической функции распределения. Контрольные вопросы. 1. Что такое случайная величина, варианта? 2. Чем отличаются дискретные и непрерывные случайные величины? 3. Что называется законом распределения случайной величины? 4. По каким формулам вычисляются числовые характеристики: а) для дискретных случайных величин; б) для непрерывных случайных величин? 5. По каким формулам вычисляются статистические показатели для сгруппированных данных? 6. Что такое функция распределения и плотность вероятности? Как они связаны? 7. На сколько классов нужно разбивать данные при группировке? 8. Чем отличается гистограмма и полигон распределения? 9. Что такое нормальное распределение, каковы его основные свойства? 10. Что характеризуют показатели асимметрии и эксцесса? 11. Каковы возможные причины многовершинности кривых распределения? 12. Что такое нормированное отклонение? 13. Какой процент вариант укладывается в пределах ±1s, ±2s, ±3s, при нормальном распределении? 14. Какие вероятности считаются доверительными? 15. Что такое уровень значимости? Какая связь между уровнем значимости и вероятностью? 16. Можно ли выражать уровень значимости в процентах? На что указывает процентная величина уровня значимости? 17. Чем отличается выборочная совокупность от генеральной? 18. Как колеблются средние арифметические отдельных выборок вокруг средней арифметической генеральной совокупности? 19. Что такое средняя квадратическая (стандартная) ошибка? Какова ее формула? 20. В каких пределах по отношению к средней арифметической выборочной совокупности может находиться средняя арифметическая генеральной совокупности? С какой вероятностью? 21. Какова зависимость между значениями средней квадратической ошибки и объемом совокупности? 22. В чем сущность нулевой гипотезы? По каким критериям можно сравнивать эмпирические и теоретические распределения? 23. Что такое критерий соответствия хи–квадрат? Напишите формулу для его вычисления. 24. Что показывает число степеней свободы? 25. Как вычисляется число степеней свободы при сравнении эмпирического ряда распределения с нормальным по критерию хи–квадрат? 26. Как вычисляются теоретические частоты при нормальном распределении? 27. При каких значениях хи–квадрата следует отклонять нулевую гипотезу? Задания для самостоятельной работы. Провести статистическую обработку результатов эксперимента. Проверить соответствие экспериментальных данных нормальному закону распределения с помощью критерия c2. Вариант 1 Рост взрослых людей 190 196 175 181 181 184 154 173 169 169 163 174 192 176 177 177 180 177 155 174 167 167 177 165 195 181 194 178 177 191 175 155 175 165 170 161 178 178 176 178 185 148 154 173 168 158 179 187 184 182 179 184 154 165 170 171 159 164 190 183 175 180 192 150 170 171 172 164 158 160 165 175 168 171 151 177 176 183 179 193 Вариант 2 Содержание Р в слюне (ммоль/л) 1,9 7,0 3,7 5,5 3,1 3,9 4,5 5,7 4,0 3,7 6,0 3,8 5,4 6,1 3,9 4,4 5,6 3,8 2,4 2,5 3,6 2,2 4,5 4,7 2,3 3,8 5,7 2,9 5,9 3,1 6,7 4,4 4,7 3,6 6,9 5,6 3,5 6,4 3,0 6,6 4,7 4,5 2,9 7,6 4,9 2,0 6,7 3,0 5,0 4,8 4,1 3,4 7,7 4,8 7,5 5,9 3,0 4,9 4,0 3,3 4,4 5,2 3,9 7,0 5,8 3,3 5,1 4,0 4,0 3,6 4,5 5,6 7,4 6,1 2,0 5,1 4,0 3,9 4,9 4,6 5,5 2,7 3,1 3,6 5,3 4,0 4,7 5,0 4,7 3,9 Вариант 3 Объем циркулирующей плазмы (мл/кг) 25 45 36 37 38 41 42 26 31 35 40 43 36 37 36 30 26 44 30 40 31 37 32 34 32 39 42 46 41 38 28 39 27 43 33 44 34 40 31 26 33 36 37 35 48 37 38 35 38 32 41 33 36 42 27 36 37 28 39 35 40 47 43 44 34 36 35 34 36 41 42 35 28 39 31 37 38 50 29 33
Вариант 4 Показатели гематокрита (эритроциты–плазма) 0,26 0,12 0,20 0,28 0,29 0,21 0,45 0,38 0,29 0,24 0,27 0,18 0,23 0,30 0,32 0,18 0,42 0,36 0,26 0,29 0,48 0,10 0,22 0,16 0,41 0,23 0,14 0,33 0,34 0,35 0,27 0,24 0,30 0,17 0,11 0,15 0,30 0,28 0,40 0,23 0,35 0,23 0,28 0,16 0,26 0,17 0,36 0,30 0,22 0,27 0,49 0,22 0,22 0,39 0,26
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.105 (0.008 с.) |

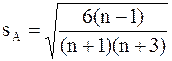 ,
, 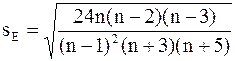 , (25)
, (25)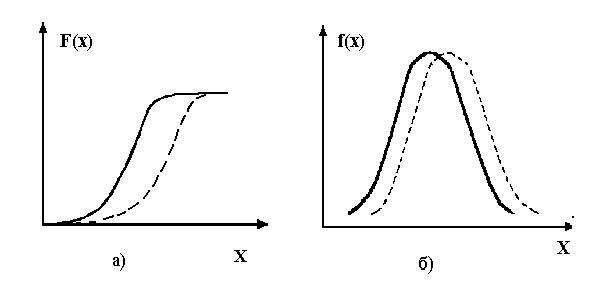
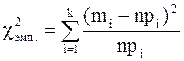 (26)
(26) , xmax=91 xmin=47
, xmax=91 xmin=47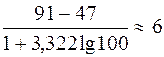
 ,
,

 ,
,
 0, если x<44
0, если x<44

 m
m
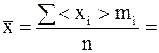 =
= 
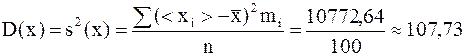


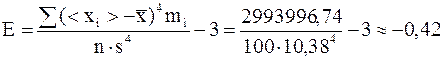


 <0,48 (2sА), êEê=ê-0,42ê<0,928 (2sЕ),
<0,48 (2sА), êEê=ê-0,42ê<0,928 (2sЕ),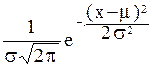
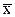 и s соответственно:
и s соответственно: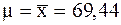 ,s=s=10,38.
,s=s=10,38.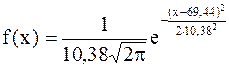

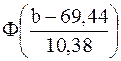 –
– 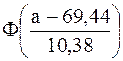
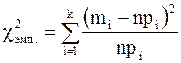
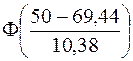 –
– 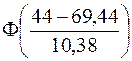 =
= x<56)=
x<56)=  –
– 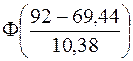 –
– 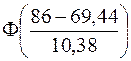 =
=