
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Руководство к практическим занятиям поСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Л.А. ШАПИРО, Н.Г. ШИЛИНА
РУКОВОДСТВО К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО МЕДИЦИНСКОЙ И БИОЛОГИЧЕСКОЙ СТАТИСТИКЕ
КРАСНОЯРСК 2003
Л.А. Шапиро, Н.Г. Шилина. Руководство к практическим занятиям по медицинской и биологической статистике. Учебное пособие для студентов медицинских вузов. – Красноярск, 2003, 94 стр. Цена договорная.
Рецензенты: Горнева Е.И., доцент кафедры высшей математики Красноярского государственного технического университета, к.т.н. Гончарова Г.Н., заведующая кафедрой СГОЗ Красноярской государственной медицинской академии д.м.н., профессор. Новиков О.М., профессор кафедры медицинского страхования, менеджмента и маркетинга Красноярской государственной медицинской академии, д.м.н.
Рекомендуется Сибирским региональным Учебно–методическим центром высшего профессионального образования в качестве учебного пособия для студентов и аспирантов медицинских вузов. Рекомендуется Учебно–методическим объединением по медицинскому и фармацевтическому образованию вузов России в качестве учебного пособия для студентов, обучающихся по специальности 040600–Сестринское дело.
Руководство предназначено для студентов и аспирантов медицинских вузов. В нем в общедоступной форме изложены необходимые для медико-биологических исследований статистические методы: группировка материала, составление вариационных рядов, вычисление и оценка выборочных показателей, корреляционный, регрессионный и дисперсионный анализ.
ПРЕДИСЛОВИЕ.
В настоящее время стремление к математическому выражению соответствующих закономерностей распространилось на все области знаний, в том числе на биологию и медицину. Важнейшим обстоятельством, определившим применение математико-статистических методов, явилось установление того, что многим медико-биологическим явлениям свойственны статистические закономерности, обнаруживаемые при изучении совокупностей. Так, многие экологические, генетические, цитологические, микробиологические, фармакологические и другие явления – массовые по своей природе. В данном руководстве изложены элементарные основы медицинской и биологической статистики в объеме, предусмотренном программой. Оно состоит из четырех основных тем: изучение нормального закона распределения случайной величины, закономерностей малых выборок, а также корреляционного, регрессионного и дисперсионного анализа. Большое внимание уделено понятию достоверности при анализе медико-биологических данных. Изложенный материал иллюстрируется конкретными примерами из различных областей биологии и медицины. К каждой теме составлены контрольные вопросы и задания для самостоятельной работы. В Приложении собраны необходимые таблицы. Руководство является специализированным, приспособленным для подготовки врача.
Таблица 1
0<P<1, При графическом способе задания на оси абсцисс откладывают значения, принимаемые этой величиной, а на оси ординат – соответствующие им вероятности (рис.1). Для непрерывной случайной величины такого графика построить нельзя, так как случайная величина имеет бесчисленное множество значений, сплошь заполняющей некоторый промежуток (рис.2).
Кроме закона распределения, дискретные и непрерывные случайные величины характеризуются числовыми характеристиками. Возраст
Рис.5. Гистограмма распределения студентов по возрасту.
Кривая, соединяющая середины прямоугольников, называется полигоном распределения. Так как при достаточно большом числе n случаев, относительная частота появления тех или иных значений случайной величины x соответствует их вероятности Р(x), то можно считать, что площади прямоугольников, составляющих гистограмму, пропорциональны вероятностям попадания случайной величины в соответствующий интервал Dx. Высота прямоугольников будет являться плотностью распределения вероятностей. Функция плотности распределения вероятностей f(х) в этом случае имеет ступенчатый характер. При достаточно большом числе интервалов на гистограмме функция распределения вероятностей приобретает плавный характер (пунктирная линия на рис.5). В пределе, при Dx Для ряда непрерывных случайных величин, сгруппированных в классы, математическое ожидание и дисперсия вычисляются по формулам (3), (5), где m – число попаданий в класс, n – общее количество величин, <xi> – средняя величина в классе. В нашем примере: Таблица 3
å=100 М(x)=21,3 D(x)=9,9
На практике ряд распределения (вариационный ряд) составляют следующим образом: 1. Из имеющихся значений признака x выбирают наименьшее (xmin), наибольшее (xmax), определяют размах распределения (xmax – xmin). 2. Определяют число классов группировки. Для определения числа классов можно воспользоваться формулой: k=1+3,32·lg n, где n – число измерений. Величину k округляют до целых чисел. 3. Определяют оптимальную величину класса (интервала группировки) Dxi= 4. Выбирают границы классов. Границы первого класса следует выбрать так, чтобы он содержал наименьшее значение, но не начинался с него, например, класс может начинаться с величины (xmin – 5. Определяют середину интервала <xi>. Задание: Для ряда измерений роста студентов сгруппировать данные по классам, определить математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить гистограмму и полигон распределения. 148 158 150 162 170 156 186 151 161 152 171 165 174 157 172 172 177 166 157 149 159 154 164 167 173 176 147 163 185 164 161 153 168 162 184 162 169 154 167 163 166 172 158 155 165 179 165 160 159 169 Нормальный закон распределения случайных величин.
Для того чтобы обрабатывать результаты экспериментов, важно знать, к какому виду распределения случайных величин относятся полученные результаты. Например, в физике распределение скоростей молекул газа при тепловом движении подчиняется распределению Максвелла. Распределение дискретных случайных величин может подчиняться биномиальному закону, для редких событий справедливо распределение Пуассона и т.д. Важное место в статистике вообще и в биологической статистике в частности, занимает нормальное распределение (распределение Гаусса). Нормальное распределение возникает тогда, когда на изменение случайной величины действует множество различных независимых факторов, каждый из которых в отдельности не имеет преобладающего значения. Многие распределения биологических признаков, характеризующиеся непрерывной вариацией, а также ошибки измерений подчиняются нормальному закону. Размещение вариант при нормальном распределении характеризуется определенными закономерностями: Параметр m характеризует математическое ожидание (среднее арифметическое) случайной величины, являясь центром распределения и наиболее вероятным значением. Изменение математического ожидания не влияет на форму кривой, а только вызывает ее смещение вдоль оси x. Параметр s характеризует изменчивость случайной величины (меру растянутости кривой вдоль оси x): чем больше s, тем больше кривая растянута. График нормальной кривой симметричен относительно прямой x=m (одинаковые по абсолютной величине отрицательные и положительные отклонения случайной величины от центра равновероятны). По мере увеличения разности (x–m) значение f(x) убывает. Это значит, что большие отклонения менее вероятны, чем малые. При (x–m) График функции нормального распределения представляет собой колоколообразную кривую (рис.6).
Рис.6. Кривая нормального распределения.
Для нормального распределения, имеющего математическое ожидание mи среднее квадратическое отклонение s, плотность распределения вероятности имеет вид: f(x) = а функция распределения вероятности равна:
Для перехода от двух параметров распределения mи s к одному, делают замену переменной: t= с помощью которой функцию (14) можно привести к виду:
Функция (16) не выражается через элементарные функции, но для нее составлены таблицы, которые называются таблицами нормального интеграла вероятности. Вероятность того, что значение случайной величины попадет в интервал от а до b: Р(a<x<b)= при этом значения функции Ф находят по таблице 1 Приложения. Для нее выполняется соотношение: Ф(–t) = 1– Ф(t). В нашем примере распределения студентов по возрасту, функция распределения будет иметь вид: F(x)= Найдем вероятность того, что на первый курс поступят вундеркинды в возрасте младше 16 лет: P(x<16)= Задание: Анализ веса 75 новорожденных детей показал, что у них в интервал от 1 до 1,9 кг попало 5 новорожденных, 2 – 2,9 кг – 25 новорожденных, 3 – 3,9 кг – 40 новорожденных, 4 – 4,9кг – 5 новорожденных. Записать функции плотности вероятности f(x) и распределения вероятностей F(x) для предполагаемого нормального распределения веса новорожденных, определить вероятность рождения недоношенного ребенка весом <2,5 кг. Функция нормального закона распределения, как правило, симметрична относительно математического ожидания. Если же варианты накапливаются преимущественно в правой или левой части ряда, то говорят об асимметрии. Мерой скошенности ряда служит коэффициент асимметрии А. Для симметричных кривых распределения А равен нулю, для правоасимметричных А>0, для левоасимметричных А<0. Асимметрия считается незначительной, если А А= Для распределений с резко выраженным пиком (островершинных) Е >0, для плосковершинных Е <0 (рис 7б).
Рис.7а. Рис.7б.
Если число измерений в некоторых классах мало, или исследуемый материал не является однородным, можно наблюдать многовершинные распределения.
Интервальные оценки.
Для изучения закономерностей вариации при нормальном распределении широко пользуются величиной нормированного отклонения t. Мы ввели этот параметр в уравнении (15) для преобразования переменных при вычислении функции распределения вероятностей. Смысл такого преобразования (нормирования) заключается в том, что за начало отсчета значений случайной величины берется математическое ожидание (среднее значение), а среднее квадратическое отклонение используется как единица измерения. Нормированное отклонение представляет собой отклонение той или иной варианты от математического ожидания,выраженное в сигмах: t= Каждая варианта характеризуется определенным значением t, указывающим ее положение в ряду значений или на кривой распределения. Так, если какая то варианта имеет значение t=1,5, это значит, что она располагается в правой части кривой на расстоянии в 1,5σ. Если варианта имеет значение t=-2,5, то она расположена в левой части кривой на расстоянии от μ в 2,5σ и т.д. Зная вариационную кривую распределения вариант по тому или иному признаку и предполагая, что распределение является нормальным, можно заранее предсказать, какой процент изученных вариант укладывается в пределах Вероятности 0,95 и 0,99 (95% и 99%), получили название доверительных вероятностей, т.е. таких, значениям которых можно достаточно доверять или которыми можно уверенно пользоваться. Доверительные вероятности, в свою очередь, определяют доверительные границы или доверительный интервал, в котором может находиться случайная величина. Из уравнения (20) можно записать выражение для интервала значений случайной величины х: Δх=±st. (21) Произведение st будет определять величину интервала, в котором может находиться случайная величина с заданной степенью вероятности. Вероятность любого отклонения от средней, как функция нормированного отклонения, определяется с помощью таблицы 2 Приложения. Геометрически величины, находящиеся в таблице, являются долями площади нормальной кривой в границах от -t до +t, выражающие в то же время и вероятность. Первая колонка слева таблицы 2 дает значения t с одним десятичным знаком, второй десятичный знак t представлен 10 столбцами, на которых вверху стоят цифры от 0 до 9. Тогда t=1,00 соответствует вероятность 0,6827 (11–я строка, 1–я цифра) и т.д. В то же время, задаваясь определенным уровнем вероятности, можно определить t. Для различных вероятностей доверительные интервалы будут следующими: Вероятности Интервалы 0,95 ±1,96s 0,99 0,999 Определенным значениям вероятностей соответствуют так называемые уровни значимости. По отношению к закономерностям нормального закона распределения, уровень значимости обозначает вероятность выхода случайной величины за пределы доверительного интервала. Если доверительную вероятность обозначить – Р, а уровень значимости – a, то a=1 – Р. Для доверительной вероятности 0,95 – уровень значимости будет равен 0,05 (5% вариант могут выйти за пределы доверительного интервала), для доверительной вероятности 0,99, a=0,01 и т.д. В медико–биологических исследованиях используются как доверительные вероятности (Р), так и уровни значимости(a).
Рассчитаем, какая доля вариант находится в вариационной кривой между -1,5s и +1,0s пользуясь таблицей 2 Приложения. В интервале между -1,5s и +1,5s находится 0,8664 всех вариант. Следовательно, в интервале между -1,5s и Задание: Рассчитайте, какая доля вариант находится в вариационной кривой между -1s и 2,8s, между Ответы: 0,839, 0,495, 0,46, 0,50, 0,0139.
Как они связаны? 7. На сколько классов нужно разбивать данные при группировке? 8. Чем отличается гистограмма и полигон распределения? 9. Что такое нормальное распределение, каковы его основные свойства? 10. Что характеризуют показатели асимметрии и эксцесса? 11. Каковы возможные причины многовершинности кривых распределения? 12. Что такое нормированное отклонение? 13. Какой процент вариант укладывается в пределах ±1s, ±2s, ±3s, при нормальном распределении? 14. Какие вероятности считаются доверительными? 15. Что такое уровень значимости? Какая связь между уровнем значимости и вероятностью? 16. Можно ли выражать уровень значимости в процентах? На что указывает процентная величина уровня значимости? 17. Чем отличается выборочная совокупность от генеральной? 18. Как колеблются средние арифметические отдельных выборок вокруг средней арифметической генеральной совокупности? 19. Что такое средняя квадратическая (стандартная) ошибка? Какова ее формула? 20. В каких пределах по отношению к средней арифметической выборочной совокупности может находиться средняя арифметическая генеральной совокупности? С какой вероятностью? 21. Какова зависимость между значениями средней квадратической ошибки и объемом совокупности? 22. В чем сущность нулевой гипотезы? По каким критериям можно сравнивать эмпирические и теоретические распределения? 23. Что такое критерий соответствия хи–квадрат? Напишите формулу для его вычисления. 24. Что показывает число степеней свободы? 25. Как вычисляется число степеней свободы при сравнении эмпирического ряда распределения с нормальным по критерию хи–квадрат? 26. Как вычисляются теоретические частоты при нормальном распределении? 27. При каких значениях хи–квадрата следует отклонять нулевую гипотезу? Задания для самостоятельной работы. Провести статистическую обработку результатов эксперимента. Проверить соответствие экспериментальных данных нормальному закону распределения с помощью критерия c2. Вариант 1 Рост взрослых людей 190 196 175 181 181 184 154 173 169 169 163 174 192 176 177 177 180 177 155 174 167 167 177 165 195 181 194 178 177 191 175 155 175 165 170 161 178 178 176 178 185 148 154 173 168 158 179 187 184 182 179 184 154 165 170 171 159 164 190 183 175 180 192 150 170 171 172 164 158 160 165 175 168 171 151 177 176 183 179 193 Вариант 2 Содержание Р в слюне (ммоль/л) 1,9 7,0 3,7 5,5 3,1 3,9 4,5 5,7 4,0 3,7 6,0 3,8 5,4 6,1 3,9 4,4 5,6 3,8 2,4 2,5 3,6 2,2 4,5 4,7 2,3 3,8 5,7 2,9 5,9 3,1 6,7 4,4 4,7 3,6 6,9 5,6 3,5 6,4 3,0 6,6 4,7 4,5 2,9 7,6 4,9 2,0 6,7 3,0 5,0 4,8 4,1 3,4 7,7 4,8 7,5 5,9 3,0 4,9 4,0 3,3 4,4 5,2 3,9 7,0 5,8 3,3 5,1 4,0 4,0 3,6 4,5 5,6 7,4 6,1 2,0 5,1 4,0 3,9 4,9 4,6 5,5 2,7 3,1 3,6 5,3 4,0 4,7 5,0 4,7 3,9 Вариант 3 Объем циркулирующей плазмы (мл/кг) 25 45 36 37 38 41 42 26 31 35 40 43 36 37 36 30 26 44 30 40 31 37 32 34 32 39 42 46 41 38 28 39 27 43 33 44 34 40 31 26 33 36 37 35 48 37 38 35 38 32 41 33 36 42 27 36 37 28 39 35 40 47 43 44 34 36 35 34 36 41 42 35 28 39 31 37 38 50 29 33
Вариант 4 Показатели гематокрита (эритроциты–плазма) 0,26 0,12 0,20 0,28 0,29 0,21 0,45 0,38 0,29 0,24 0,27 0,18 0,23 0,30 0,32 0,18 0,42 0,36 0,26 0,29 0,48 0,10 0,22 0,16 0,41 0,23 0,14 0,33 0,34 0,35 0,27 0,24 0,30 0,17 0,11 0,15 0,30 0,28 0,40 0,23 0,35 0,23 0,28 0,16 0,26 0,17 0,36 0,30 0,22 0,27 0,49 0,22 0,22 0,39 0,26
Сводка основных формул. 1. Средняя арифметическая выборки: 2. Дисперсия: D(x)= 3. Среднее квадратическое отклонение: 4. Стандартная ошибка (средняя квадратическая ошибка): 5. Критерий нормированного отклонения (по Стьюденту): t= 6. Доверительный интервал: tp,n× 7. Критерий tэксп для определения достоверности средней арифметической одной выборки: 8. Критерий tэксп разности средних арифметических двух выборок: а) n б) n<30
Контрольные вопросы. 1. Отличаются ли друг от друга по закономерностям случайной вариации выборочная и генеральная совокупности? 2. Как колеблются средние арифметические отдельных выборок вокруг средней арифметической генеральной совокупности? 3. Что такое средняя квадратическая (стандартная) ошибка? По какой формуле она определяется? 4. Какова зависимость между значением стандартной ошибки и объемом совокупности? 5. В каких пределах по отношению к средней арифметической выборочной совокупности может находится средняя арифметическая генеральной совокупности? С какой вероятностью? 6. Изменяется ли доверительный интервал для 7. В каких случаях применяется распределение Стьюдента? 8. Как определяется критерий нормированного отклонения по Стьюденту? 9. Как пользуясь таблицами Стьюдента: а) определить t для заданного уровня вероятности, зная число опытов n; б) определить вероятность по известным t и числу опытов n. 10. Какой критерий используется для проверки достоверности статистических показателей? 11. Как определить достоверность средней арифметической одной выборки? 12. Как определить достоверность разности средних арифметических: а) зависимых выборок; б) независимых выборок? 13. Как отличается определение достоверности разности средних арифметических для независимых выборок в случае: а)количество вариант в выборке n б) количество вариант в выборке n<30?
Задания для самостоятельной работы.
1. Рассчитать основные статистические характеристики ( 2. Для данных выборок определить доверительный интервал для генеральной средней: а) с вероятностью р=0,95; б) с вероятностью р=0,99. 3. Рассчитать достоверность различия двух независимых выборок (таблица 1). 4. Рассчитать достоверность различия двух связанных выборок (таблица 2) разностным методом. Записать вывод. Вариант 1. Скорость десневой экссудатации у детей (мл/сутки) Таблица 1
Скорость не стимулированного слюноотделения у детей (мл/мин.) Таблица 2
Вариант 2. Калий мочи (г/сутки) Таблица 1
Норадреналин мочи (мкг/сутки) при грудной жабе. Таблица 2
Вариант 3. Содержание адренокортикотропного гормона (мл.ед) Таблица 1
Микрошероховатость поверхности эмали после воздействия кислотой (Со ОЭДФ) Таблица 2
Вариант 4. Свободный гепарин крови Таблица 1
Микрошероховатость поверхности эмали после воздействия ортофосфорной кислотой Таблица 2
Вариант 5. Связанный холестерин крови (мг%) Таблица 1
Содержание трийодтиронина (мг/мл) при тиреотоксикозе Таблица 2
Вариант 6. Показатели гемоглобина пришлого населения Заполярья (г/л) Таблица 1
Количество плазматических недозрелых клеток в слизистой толстой кишки (%) при дизентерии. Таблица 2
Тема 3. Основы корреляционного анализа
В медицинских и биологических исследованиях можно наблюдать наличие связей между отдельными признаками, явлениями. Например, пульс может изменяться в зависимости от артериального давления, дыхания, температуры тела и т.д. Существует две категории связей или зависимостей между признаками: функциональные и корреляционные (статистические). При функциональных зависимостях каждому значению одной переменной величины соответствует одно вполне определенное значение другой переменной (функции). Корреляционные (статистические) связи характеризуются тем, что численному значению одной переменной соответствует много значений (распределение) другой переменной. Функциональная связь имеет место по отношению к каждому отдельному наблюдению. Корреляционная связь проявляется лишь в среднем для всей совокупности наблюдений. В отношении отдельных наблюдений она является неполной и неточной. Например, существует связь между ростом и весом человека, однако полного соответствия между значениями этих признаков нет. В некоторых случаях более высокие люди могут иметь меньший вес и наоборот. Функциональную связь можно выразить в виде уравнения, где изменению аргумента будет соответствовать вполне определенное приращение функции. При корреляции можно наблюдать только совместное изменение наблюдаемых признаков. Например, при увеличении одного признака другой признак может тоже увеличиваться или наоборот, уменьшаться. Соответственно, корреляционная связь может быть положительной (прямой), когда оба признака меняются в одном направлении и отрицательной (обратной), когда развитие одного явления связано с ослаблением другого. Корреляционные зависимости наблюдаются между очень многими признаками организмов – морфологическими, физиологическими и т.д., поэтому их оценка имеет большое практическое значение. Изучение корреляционных зависимостей производится табличным, графическим и аналитическим методами. При табличном изучении корреляционных связей зависимость между величинами х и у задается двумерной таблицей, называемой корреляционной решеткой. Рассмотрим два случая: 1. Для небольшого количества измерений, не сгруппированных в классы следует выписать попарно все показатели: сначала первый показатель – обозначим его х; затем связанный с ним второй показатель у; количество пар показателей х и у обозначим N. Например:
2. Для большого количества наблюдений. В этом случае разбиваем на классы как ряд х, так и ряд у. Определив классы, следует построить корреляционную решетку. На двух сторонах квадрата (вверху по горизонтали и слева по вертикали) наносят значения классов обоих рядов. По горизонтали классы записывают слева направо от меньших значений к большим, по вертикали сверху вниз от меньших к большим. В макет корреляционной решетки следует занести показатели для всех обследованных одновременно по обоим признакам. Например, цифра 1 в первой клетке обозначает, что только один человек имеет артериальное давление от 60 до 70 и пульс от 30 до 40. Суммы всех опытов в горизонтальных строках пишутся справа(my), суммы всех опытов в вертикальных столбцах пишутся внизу (mx). Справа внизу в угловой клетке записывается сумма всех опытов (72). Она относится как к ряду х так и к ряду у.
Корреляционная решетка для зависимости частоты сердечных сокращений (ЧСС) от артериального давления (АД).
При графическом способе на плоскость попарно наносятся точки, соответствующие (х) и (у). Эти точки занимают определенную область, называемую корреляционным полем. На рисунках 1(а–е) показано возможное распределение вариант по отдельным клеткам корреляционной решетки при корреляциях, отличающихся по знаку и величине. Если варианты расположены в решетке равномерно в овале и разброс точек велик, то признаки х и у варьируют независимо, корреляция между ними отсутствует (рис.1а). Если корреляционное поле имеет вид эллипса со сгущением точек вокруг главной диагонали, то между признаками х и у имеется связь (рис.1б, в, г, д, е). По тому, к какой диагонали происходит сгущение точек можно судить о знаке корреляции. На рис.1б, в, д – связь положительная, на рис.1г, е – связь отрицательная. По степени сгущения точек можно судить о величине коэффициента корреляции. Если варианты расположены по диагонали, зависимость между х и у становится функциональной, то есть каждому значению х соответствует определенное значение у и наоборот.
а) б)
r=0 r=+0,5
в) г)
r=+0,8 r=–0,5
д) е)
r=+1 r=–1
Рис 1. Распределение вариант в корреляционных решетках при корреляции, отличающейся по знаку и величине.
Расположение вариант в корреляционной решетке не всегда бывает таким правильным. Нахождение одной или нескольких вариант в стороне от овала может резко изменить предполагаемое значение коэффициента корреляции. Поэтому для более точного измерения степени связи необходимо аналитическое вычисление коэффициента корреляции (r). По законам случайной вариации, если бы разброс экспериментальных данных равнялся нулю, то точки корреляционного поля сконцентрировались в условном центре с координатами, равным средним значениям:
При реальных корреляциях между х и у мерой рассеяния могут служить дисперсии или средние квадратические отклонения sx и sy: sх= <
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.015 с.) |



 Рис.1.Дискретное распределение. Рис.2.Непрерывное распределение.
Рис.1.Дискретное распределение. Рис.2.Непрерывное распределение.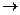 0 построенное нами распределение дискретной случайной величины стремится к распределению непрерывной случайной величины. Таким образом, распределение непрерывной случайной величины можно приближенно заменить распределением дискретной случайной величины.
0 построенное нами распределение дискретной случайной величины стремится к распределению непрерывной случайной величины. Таким образом, распределение непрерывной случайной величины можно приближенно заменить распределением дискретной случайной величины. =3,15
=3,15 . Эту величину также можно округлять соответственно точности значений x.
. Эту величину также можно округлять соответственно точности значений x. ). Последующие классы образуются добавлением величины интервала Dxi. Если нижняя граница класса совпадает с верхней границей предыдущего класса, это значение следует отнести к данному классу. Например, [1–2), [2–3) и т.д.
). Последующие классы образуются добавлением величины интервала Dxi. Если нижняя граница класса совпадает с верхней границей предыдущего класса, это значение следует отнести к данному классу. Например, [1–2), [2–3) и т.д. значение f(x) стремится к нулю, но никогда его не достигает.
значение f(x) стремится к нулю, но никогда его не достигает.
 , (13)
, (13) (14)
(14) , dx= s dt, (15)
, dx= s dt, (15) (16)
(16) (17)
(17)
 dx (18)
dx (18)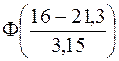 =Ф(–1,6825)=1–0,9535=0,0465=4,65%.
=Ф(–1,6825)=1–0,9535=0,0465=4,65%. 0,2. При А
0,2. При А  0,5 скошенность кривой считается сильной (рис.7а). Показатель эксцесса (Е) характеризует вершину кривой распределения.
0,5 скошенность кривой считается сильной (рис.7а). Показатель эксцесса (Е) характеризует вершину кривой распределения. ; E=
; E= 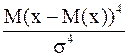 – 3 (19)
– 3 (19)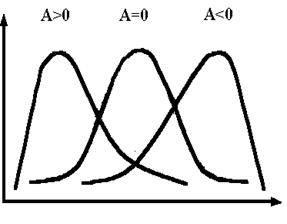

 , отсюда х – μ=σt. (20)
, отсюда х – μ=σt. (20) 1σ, в пределах
1σ, в пределах 

 : (0,8664:2)=0,4332. Аналогично, в интервале
: (0,8664:2)=0,4332. Аналогично, в интервале 

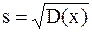



 30
30 
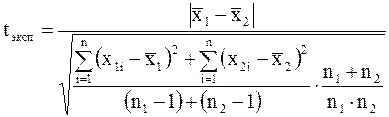
 при разных величинах n?
при разных величинах n? х(АД)
у
(ЧСС)
х(АД)
у
(ЧСС)


 ,
, 


