
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значения t при различных уровнях значимости (Р)Содержание книги
Поиск на нашем сайте
… 5. Определим доверительный интервал для уровня Р=0,95 в нашем примере. По таблицам Стьюдента (таблица 4 Приложения) находим t для уровня 0,95 и числа степеней свободы 4: t=2,78, следовательно: m=108,6±2,78×8,57=108,6±23,82 или 84,78£m£132,42. Роль среднеквадратической ошибки в статистическом анализе очень велика. Во–первых, она позволяет определить границы для показателей генеральной совокупности, а во–вторых, дает возможность определить степень достоверности различных статистических показателей, например, средней арифметической величины и разницы средних арифметических величин двух выборок. В обоих случаях алгоритм определения достоверности одинаков: определяется экспериментальный критерий нормированного отклонения tэксп для разности средней арифметической величины выборки и генеральной средней или средних арифметических двух выборок; сравнивается полученный экспериментальный критерий с tтабл для доверительной вероятности Р=0,95. Если tэксп больше либо равно tтабл, то средняя арифметическая выборки достоверно отражает генеральную среднюю, или две выборки отличаются с вероятностью, большей либо равной 0,95. Рассмотрим определение достоверности средней величины выборки. Мерой достоверности является критерий нормированного отклонения, определяемый по формуле (6):
Возникает вопрос, откуда взять величину генеральной совокупности (m)? Возможны два варианта: 1. Среднее арифметическое генеральной совокупности представляет собой определенную, отличающуюся от нуля величину, значение которой можно предположить по другим данным. В нашем примере, если ранее изучалась ЧСС в других выборках, то среднее арифметическое генеральной совокупности будет равно средней арифметической средних этих выборок. Предположим, получилось число 86. Тогда: tэксп= Определим по таблицам Стьюдента вероятность определения средней арифметической для степеней свободы равной 4 и t=2,64. Значение Р>0,95, следовательно, достоверность вполне достаточна. 2. Предполагается, что действие изучаемого фактора может быть и положительным, и отрицательным. Тогда m следует приравнять 0. В этом случае: t= Средние арифметические величины, вычисленные для большинства биологических показателей, чаще всего достоверны, если ряд не слишком растянут, но если варианты в ряду имеют и положительный, и отрицательный знак, определение достоверности
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

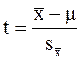
 = 2,64
= 2,64 .
. обязательно. Проиллюстрируем это на примере сравнения парных (зависимых) выборок.
обязательно. Проиллюстрируем это на примере сравнения парных (зависимых) выборок.


