
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двух независимых выборочных совокупностей.Содержание книги
Поиск на нашем сайте
Если эксперимент проводится на различных группах, то возникает вопрос: из одной генеральной совокупности или из разных взяты эти выборки? Если выборки взяты из одной генеральной совокупности, то разница их средних арифметических будет статистически незначима. Если выборки принадлежат к различным генеральным совокупностям, то разница их средних арифметических будет статистически достоверной (P Для установления разницы между средними арифметическими рассчитаем нормированное отклонение t:
Числителем является, взятая по абсолютной величине, разница между средними арифметическими двух групп (сокращенно обозначили d). В знаменателе – средняя квадратическая ошибка этой разницы Если n<30, ошибка разницы определяется по формуле:
Например, определялось содержание белка в сыворотке крови в группе здоровых людей (n1=5) и больных гепатитом (n2=6). Определим, достоверна ли разница в содержании белка у здоровых людей и больных гепатитом. Для вычислений составим таблицу: Таблица 2 Норма Гепатит
s1=0,212 s2=0,197
sd= Определим tтабл для P=0,95 и числа степеней свободы в двух группах: (n1–1)+(n2–1)=9; tтабл=2,26, tэксп>tтабл (2,67>2,26). Следовательно, вероятность различия P>0,95. Полученное содержание белка в норме: 6,866 Если численность выборок достаточно большая (n sd= Допустим, мы хотим сравнить действие двух лекарственных препаратов, снижающих артериальное давление. Группа больных, принимающих 1–й препарат, состояла из 40 человек, другая группа – из 50. Среднее систолическое артериальное давление в 1й группе составляло 150 tэксп = По таблице нормального интеграла вероятности (таблица 2 Приложения) находим вероятность P=0,22. Разница средних арифметических недостоверна, следовательно, сделать вывод какой лекарственный препарат эффективнее, нельзя. При отсутствии таблиц можно исходить из правила трех сигм: если разница d превышает свою ошибку почти в 3 раза, она достоверна с вероятностью не менее 0,99. Если n>30,то tэксп=1,96 гарантирует достоверность разницы с вероятностью 0,95.
Сводка основных формул. 1. Средняя арифметическая выборки: 2. Дисперсия: D(x)= 3. Среднее квадратическое отклонение: 4. Стандартная ошибка (средняя квадратическая ошибка): 5. Критерий нормированного отклонения (по Стьюденту): t= 6. Доверительный интервал: tp,n× 7. Критерий tэксп для определения достоверности средней арифметической одной выборки: 8. Критерий tэксп разности средних арифметических двух выборок: а) n б) n<30
Контрольные вопросы. 1. Отличаются ли друг от друга по закономерностям случайной вариации выборочная и генеральная совокупности? 2. Как колеблются средние арифметические отдельных выборок вокруг средней арифметической генеральной совокупности? 3. Что такое средняя квадратическая (стандартная) ошибка? По какой формуле она определяется? 4. Какова зависимость между значением стандартной ошибки и объемом совокупности? 5. В каких пределах по отношению к средней арифметической выборочной совокупности может находится средняя арифметическая генеральной совокупности? С какой вероятностью? 6. Изменяется ли доверительный интервал для 7. В каких случаях применяется распределение Стьюдента? 8. Как определяется критерий нормированного отклонения по Стьюденту? 9. Как пользуясь таблицами Стьюдента: а) определить t для заданного уровня вероятности, зная число опытов n; б) определить вероятность по известным t и числу опытов n. 10. Какой критерий используется для проверки достоверности статистических показателей? 11. Как определить достоверность средней арифметической одной выборки? 12. Как определить достоверность разности средних арифметических: а) зависимых выборок; б) независимых выборок? 13. Как отличается определение достоверности разности средних арифметических для независимых выборок в случае: а)количество вариант в выборке n б) количество вариант в выборке n<30?
Задания для самостоятельной работы.
1. Рассчитать основные статистические характеристики ( 2. Для данных выборок определить доверительный интервал для генеральной средней: а) с вероятностью р=0,95; б) с вероятностью р=0,99. 3. Рассчитать достоверность различия двух независимых выборок (таблица 1). 4. Рассчитать достоверность различия двух связанных выборок (таблица 2) разностным методом. Записать вывод. Вариант 1. Скорость десневой экссудатации у детей (мл/сутки) Таблица 1
Скорость не стимулированного слюноотделения у детей (мл/мин.) Таблица 2
Вариант 2. Калий мочи (г/сутки) Таблица 1
Норадреналин мочи (мкг/сутки) при грудной жабе. Таблица 2
Вариант 3. Содержание адренокортикотропного гормона (мл.ед) Таблица 1
Микрошероховатость поверхности эмали после воздействия кислотой (Со ОЭДФ) Таблица 2
Вариант 4. Свободный гепарин крови Таблица 1
Микрошероховатость поверхности эмали после воздействия ортофосфорной кислотой Таблица 2
Вариант 5. Связанный холестерин крови (мг%) Таблица 1
Содержание трийодтиронина (мг/мл) при тиреотоксикозе Таблица 2
Вариант 6. Показатели гемоглобина пришлого населения Заполярья (г/л) Таблица 1
Количество плазматических недозрелых клеток в слизистой толстой кишки (%) при дизентерии. Таблица 2
Тема 3. Основы корреляционного анализа
В медицинских и биологических исследованиях можно наблюдать наличие связей между отдельными признаками, явлениями. Например, пульс может изменяться в зависимости от артериального давления, дыхания, температуры тела и т.д. Существует две категории связей или зависимостей между признаками: функциональные и корреляционные (статистические). При функциональных зависимостях каждому значению одной переменной величины соответствует одно вполне определенное значение другой переменной (функции). Корреляционные (статистические) связи характеризуются тем, что численному значению одной переменной соответствует много значений (распределение) другой переменной. Функциональная связь имеет место по отношению к каждому отдельному наблюдению. Корреляционная связь проявляется лишь в среднем для всей совокупности наблюдений. В отношении отдельных наблюдений она является неполной и неточной. Например, существует связь между ростом и весом человека, однако полного соответствия между значениями этих признаков нет. В некоторых случаях более высокие люди могут иметь меньший вес и наоборот. Функциональную связь можно выразить в виде уравнения, где изменению аргумента будет соответствовать вполне определенное приращение функции. При корреляции можно наблюдать только совместное изменение наблюдаемых признаков. Например, при увеличении одного признака другой признак может тоже увеличиваться или наоборот, уменьшаться. Соответственно, корреляционная связь может быть положительной (прямой), когда оба признака меняются в одном направлении и отрицательной (обратной), когда развитие одного явления связано с ослаблением другого. Корреляционные зависимости наблюдаются между очень многими признаками организмов – морфологическими, физиологическими и т.д., поэтому их оценка имеет большое практическое значение. Изучение корреляционных зависимостей производится табличным, графическим и аналитическим методами. При табличном изучении корреляционных связей зависимость между величинами х и у задается двумерной таблицей, называемой корреляционной решеткой. Рассмотрим два случая: 1. Для небольшого количества измерений, не сгруппированных в классы следует выписать попарно все показатели: сначала первый показатель – обозначим его х; затем связанный с ним второй показатель у; количество пар показателей х и у обозначим N. Например:
2. Для большого количества наблюдений. В этом случае разбиваем на классы как ряд х, так и ряд у. Определив классы, следует построить корреляционную решетку. На двух сторонах квадрата (вверху по горизонтали и слева по вертикали) наносят значения классов обоих рядов. По горизонтали классы записывают слева направо от меньших значений к большим, по вертикали сверху вниз от меньших к большим. В макет корреляционной решетки следует занести показатели для всех обследованных одновременно по обоим признакам. Например, цифра 1 в первой клетке обозначает, что только один человек имеет артериальное давление от 60 до 70 и пульс от 30 до 40. Суммы всех опытов в горизонтальных строках пишутся справа(my), суммы всех опытов в вертикальных столбцах пишутся внизу (mx). Справа внизу в угловой клетке записывается сумма всех опытов (72). Она относится как к ряду х так и к ряду у.
Корреляционная решетка для зависимости частоты сердечных сокращений (ЧСС) от артериального давления (АД).
При графическом способе на плоскость попарно наносятся точки, соответствующие (х) и (у). Эти точки занимают определенную область, называемую корреляционным полем. На рисунках 1(а–е) показано возможное распределение вариант по отдельным клеткам корреляционной решетки при корреляциях, отличающихся по знаку и величине. Если варианты расположены в решетке равномерно в овале и разброс точек велик, то признаки х и у варьируют независимо, корреляция между ними отсутствует (рис.1а). Если корреляционное поле имеет вид эллипса со сгущением точек вокруг главной диагонали, то между признаками х и у имеется связь (рис.1б, в, г, д, е). По тому, к какой диагонали происходит сгущение точек можно судить о знаке корреляции. На рис.1б, в, д – связь положительная, на рис.1г, е – связь отрицательная. По степени сгущения точек можно судить о величине коэффициента корреляции. Если варианты расположены по диагонали, зависимость между х и у становится функциональной, то есть каждому значению х соответствует определенное значение у и наоборот.
а) б)
r=0 r=+0,5
в) г)
r=+0,8 r=–0,5
д) е)
r=+1 r=–1
Рис 1. Распределение вариант в корреляционных решетках при корреляции, отличающейся по знаку и величине.
Расположение вариант в корреляционной решетке не всегда бывает таким правильным. Нахождение одной или нескольких вариант в стороне от овала может резко изменить предполагаемое значение коэффициента корреляции. Поэтому для более точного измерения степени связи необходимо аналитическое вычисление коэффициента корреляции (r). По законам случайной вариации, если бы разброс экспериментальных данных равнялся нулю, то точки корреляционного поля сконцентрировались в условном центре с координатами, равным средним значениям:
При реальных корреляциях между х и у мерой рассеяния могут служить дисперсии или средние квадратические отклонения sx и sy: sх= Простейшей характеристикой Gx,y связи между случайными величинами х и у служит математическое ожидание произведения отклонений х и у от условного центра. Напомним, что математическое ожидание случайной величины х принимающей n значений с вероятностями P1, P2, P3 ,…,Pn, равно: Следовательно: Gx,y = Эта характеристика носит название ковариации или момента связи и может быть вычислена для выборки из n опытов как: Gx,y = Коэффициентом корреляции называется безразмерная величина r: r = Так как отклонение тех или других вариант от их средней арифметической, выраженной в долях среднего квадратического отклонения, представляет собой нормированное отклонение: tx = то формулу (5) можно представить в виде: r = Выражая отклонение отдельных вариант от средних арифметических по обоим признакам одновременно, можно сопоставить вариацию по обоим признакам. Рассмотрим зависимость между ростом и весом в примере 1. Вычислим
Вычислим для каждой варианты tx и ty, например: tx1 = ty1 =
Чем теснее связана вариация по этим двум признакам, тем чаще совпадут значения t обоих признаков и по знаку, и по количественному значению. Причем разные единицы измерения (см) и (кг) не имеют значения. Места, занимаемые ими в вариационных рядах, будут примерно одинаковыми. Наоборот, при отсутствии корреляции совпадение величин t по обоим признакам будет чисто случайным. При статистических оценках связи случайных величин (х) и (у) по заданным выборкам используют различные рабочие формулы, полученные путем алгебраического преобразования числителя и знаменателя формулы (7). Если не рассчитывались средние арифметические величины и средние квадратические отклонения, можно воспользоваться формулой:
Коэффициент корреляции изменяется от +1 до –1. Отрицательные значения указывают на обратную зависимость между величинами х и у (возрастание одной при убывании другой). Прямая связь между величинами существует при положительных значениях коэффициента корреляции. Корреляция будет полной при r = 1 и отсутствует при r = 0. Практически считается, что при r < 0,4 связь отсутствует, при 0,4 £ r £ 0,7 имеется слабая связь. Тесная взаимосвязь между случайными величинами или процессами х и у имеется при 0,7 £ r £ 1. Для вычисления коэффициента корреляции в нашем примере по формуле (8) составим таблицу:
Для удобства заменим суммы в формуле буквами латинского алфавита:
r= Вывод: Между ростом и весом имеется тесная положительная взаимосвязь. С увеличением роста увеличивается вес. Полученный коэффициент корреляции является выборочным, поэтому он имеет свою ошибку – “ошибку” выборочности. Эта ошибка является мерой расхождения между коэффициентом корреляции выборки (r) и коэффициентом корреляции генеральной совокупности (обозначим его r). Согласно нулевой гипотезе предполагается, что в генеральной совокупности нет связи между варьирующими признаками (r=0). Тогда критерий нормированного отклонения: tэксп= При значении tэксп, соответствующим вероятностям sr = тогда tэксп = В нашем примере: sr= По таблице Стьюдента (таблица 4 Приложения) находим для Р=0,95 (a=0,05) и числа степеней свободы df=7 (df=n–2 т.к. 2 выборки) tтабл=2,37. tэксп>tтабл, следовательно значение коэффициента корреляции достоверно. Мы рассмотрели случай простой корреляции между двумя признаками для малого числа наблюдений. Однако вариация любого признака у человека или животных может быть связана с вариацией многих факторов. В этом случае определяют коэффициенты множественной или частной корреляции. Коэффициент корреляции указывает лишь на степень связи в вариации двух переменных величин, но не дает возможности судить о том, как количественно меняется одна величина по мере изменения другой. На этот вопрос позволяет ответить другой метод изучения связи между признаками – метод регрессии. При изучении связи между двумя признаками х и у с помощью метода регрессии можно установить, как количественно меняется один признак при изменении другого на единицу. Проведение регрессионого анализа можно разделить на три этапа: выбор формы зависимости (типа уравнения); вычисление коэффициентов выбранного уравнения; оценка достоверности полученного уравнения. Соответственно связи между изучаемыми признаками различают простую и множественную, линейную и нелинейную регрессию. Для того чтобы выбрать тип уравнения регрессии, необходимо проанализировать тесноту и характер связи (корреляции), графики эмпирической зависимости между переменными, биологическую сущность изучаемого явления. При простой корреляции изучается зависимость между изменчивостью двух признаков х и у. Так как изменяются две величины, то регрессия может быть двусторонней: определение изменения у по изменению х и определение изменения х по изменению у. В медико–биологических исследованиях часто встречаются случаи, когда один признак (у) свободно варьирует, а второй является более фиксированным, т.е. такой свободной вариацией не обладает. Примером могут служить так называемые ряды динамики или временные ряды, показывающие изменение признаков во времени, регрессия таких рядов оказывается односторонней. Какую величину принимать за x или y, зависит от условий эксперимента. Например, вес щитовидной железы у человека можно определить только после операции. Однако имеется тесная связь между площадью скеннографического изображения (при введении радиоактивных изотопов) и весом этого органа. Зная уравнение регрессии, можно по площади скеннограммы определить вес щитовидной железы – важного диагностического признака. Рассмотрим случай линейной регрессии. Уравнением регрессии у по х называется уравнение вида
j а x Рис.2 График линейной зависимости. Коэффициент a – начальная ордината, определяет значение у при х = 0. Графически это отрезок, отсекаемый прямой по оси y. Одним из простых способов вычисления коэффициентов уравнения регрессии (не только линейной) является метод наименьших квадратов. Сущность его состоит в том, что наилучшим считается положение линии регрессии, при котором сумма квадратов отклонений эмпирических точек по ординатам от теоретических (расчетных) минимальна. Математически это условие записывается в виде:
где уi – экспериментальные точки; у(хi) – зависимость у(хi)=а+bхi Для выполнения условия (12) нужно приравнять нулю частные производные:
что дает для определения неизвестных коэффициентов а и b систему линейных уравнений:
Решение этой системы:
Коэффициент b носит название коэффициента регрессии. Для удобства введем обозначения:
тогда:
Рассмотрим основные этапы проведения регрессионного анализа на примере зависимости веса щитовидной железы (у) от площади скеннографического изображения (х).
Перепишем ряды в порядке возрастания х:
у 12 23 41 59 62 95 102 122 203 270 х 11 17 25 32 33 44 46 52 73 89
Построим эмпирическую кривую распределения, выбрав соответствующий масштаб:
Рис.3. Эмпирическая кривая регрессии. Для вычисления коэффициента a и b составим таблицу:
Уравнение регрессии будет иметь вид: у = -41,71 +3,332 х Для построения теоретической линии регрессии достаточно рассчитать по этому уравнению несколько точек: при х = 0; у =-41,71 х =10; у = -8,39 х=90; у= 258,16
Рис.4. Теоретическая линия регрессии. Уравнение регрессии позволяет вычислять теоретические (вероятные) значения зависимой переменной по заданным значениям независимых переменных в области их изменения. Как правило, оно применяется только внутри этой области. Например, если у больного площадь скеннографического изображения равна 30 см2, то вес щитовидной железы равен: y=-41,71+3,332×30=58,25г. Так как уравнение регрессии определялось нами на основе выборочной совокупности, оно может в той или иной мере представлять уравнение истинной регрессии в генеральной совокупности. Коэффициенты а и b, как и другие статистические параметры, имеют ошибки выборочности. В более простом случае для оценки качества полученного уравнения регрессии можно воспользоваться разностным методом, используемом нами для оценки средних арифметических парных выборок (Тема 2). Вычислим разности между эмпирическими значениями уi эмп и теоретическими уi теор, рассчитанные по уравнению регрессии. Найдем разности этих значений d=yiэмп–уiтеор. Рассчитаем статистические характеристики разностного ряда: dср
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.011 с.) |

 0,95).
0,95). (10)
(10) , сокращенно sd. Вычисление средней квадратической ошибки разности средних арифметических sd отличается для численности в выборках n<30 или n
, сокращенно sd. Вычисление средней квадратической ошибки разности средних арифметических sd отличается для численности в выборках n<30 или n  (11)
(11)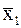

 =0,095
=0,095  =0,08
=0,08 =0,123, t эксп. =
=0,123, t эксп. =  = 2,67
= 2,67 0,095 cтатистически достоверно отличается от содержания белка в крови при гепатите: 7,195
0,095 cтатистически достоверно отличается от содержания белка в крови при гепатите: 7,195 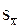 для каждой выборки. Средняя ошибка разницы в этом случае определяется по формуле:
для каждой выборки. Средняя ошибка разницы в этом случае определяется по формуле: ; (12)
; (12) =0,277
=0,277 

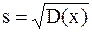




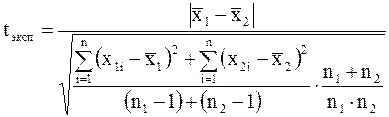
 при разных величинах n?
при разных величинах n? , D, s,
, D, s,  х(АД)
у
(ЧСС)
х(АД)
у
(ЧСС)


 ,
,  , sy=
, sy=  (2)
(2) .
. . (3)
. (3) . (4)
. (4)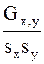 (5)
(5) , ty =
, ty =  , (6)
, (6) (7)
(7)
 168,55,
168,55,  =64,33, sx=6,46, sy=3,9
=64,33, sx=6,46, sy=3,9 =–1,63,
=–1,63, =–1,36 и т.д. Сопоставим значения tx и ty:
=–1,36 и т.д. Сопоставим значения tx и ty: (8)
(8)

 ,
,  ,
,  ,
,  ,
,  тогда формула (8) примет вид:
тогда формула (8) примет вид: =
= 
 =0,912864
=0,912864 (9)
(9) ), можно считать нулевую гипотезу отвергнутой, т.е. признать данное значение r достоверным. Для малых выборок (n<30) ошибку коэффициента корреляции sr можно определить по формуле:
), можно считать нулевую гипотезу отвергнутой, т.е. признать данное значение r достоверным. Для малых выборок (n<30) ошибку коэффициента корреляции sr можно определить по формуле: , где n – число пар измерений. (10)
, где n – число пар измерений. (10) (11)
(11) =0,154, tэксп=
=0,154, tэксп=  =5,9
=5,9 =f (х), устанавливающее зависимость между значениями независимой переменной х и условными средними зависимой переменной
=f (х), устанавливающее зависимость между значениями независимой переменной х и условными средними зависимой переменной  , вычисленное для конкретного значения х. Например, с весом х=60 кг может встретиться три человека с ростом: 160, 166 и 164 см. Условная средняя для х=60 будет равна (160+166+164):3=163,33. Если коэффициент корреляции достоверен и близок к единице, а график эмпирической зависимости – к прямой линии, то зависимость между х и у линейная и выражается уравнением: у = а + bx. Коэффициент b характеризует скорость изменения зависимой переменной у при изменении переменной х и равен тангенсу угла наклона прямой к оси х: b=tg
, вычисленное для конкретного значения х. Например, с весом х=60 кг может встретиться три человека с ростом: 160, 166 и 164 см. Условная средняя для х=60 будет равна (160+166+164):3=163,33. Если коэффициент корреляции достоверен и близок к единице, а график эмпирической зависимости – к прямой линии, то зависимость между х и у линейная и выражается уравнением: у = а + bx. Коэффициент b характеризует скорость изменения зависимой переменной у при изменении переменной х и равен тангенсу угла наклона прямой к оси х: b=tg 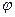 (рис.2).
(рис.2). y
y (12)
(12)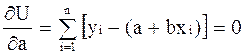 ;
;  , (13)
, (13) 

 (14)
(14)
 (15)
(15)  ;
;  ;
;  ;
;  ;
;  ,
, ,
,  .
.

 ;
; 

 . Если tэксп < tтабл для числа степеней свободы n–1 и р=0,95, то различие сравниваемых рядов несущественно, т.е. уравнение регрессии соответствует истинному уравнению в генеральной совокупности.
. Если tэксп < tтабл для числа степеней свободы n–1 и р=0,95, то различие сравниваемых рядов несущественно, т.е. уравнение регрессии соответствует истинному уравнению в генеральной совокупности.  943,11
943,11



