
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Малых выборок. Распределение Стьюдента.Содержание книги
Поиск на нашем сайте
В результате медико–биологических экспериментов исследователи получают данные, которые группируют в статистические ряды. Первым этапом исследования статистических рядов является ответ на вопрос, к какому виду распределения относятся полученные результаты. В зависимости от предполагаемого вида распределения производится вычисление основных статистических характеристик: средней арифметической величины (математического ожидания), дисперсии, среднего квадратического отклонения. Идеальным экспериментом является изучение совокупности всех объектов для решения поставленной задачи, то есть генеральной совокупности. В действительности число членов такой совокупности может быть бесконечно большим, поэтому на практике изучают выборочные совокупности из генеральной. В этом случае необходимо ответить на вопрос, насколько параметры данной выборки соответствуют параметрам генеральной совокупности, то есть вычисляя параметры конкретной выборки, дать оценку соответствующих параметров генеральной совокупности. Например, измеряя рост студентов 1–го курса в одной группе, определить интервал, в котором может варьировать рост всех студентов первого курса. Если взять несколько выборок (студенческих групп), то средние арифметические этих выборок, при числе членов каждой выборки более 30, будут распределяться вокруг генеральной средней по нормальному закону. При определении доверительного интервала для генеральной средней в этом случае нужно пользоваться статистическими таблицами для нормального интеграла вероятностей (таблица 2 Приложения). Если число членов в выборке мало (меньше 30), то возникает сомнение в возможности оценки по таким выборкам параметров генеральной совокупности. Оценку закономерностей распределения средних арифметических выборок с малым числом наблюдений дал английский математик Госсет (псевдоним Стьюдент). Полученное им распределение вероятностей получило название t – распределения Стьюдента. Рассмотрим основные этапы обработки малой выборки с использованием распределения Стьюдента. В качестве обозначений примем: m – среднее арифметическое, D – дисперсия (s2), s – среднее квадратическое отклонение генеральной совокупности, Пусть дан ряд значений частоты сердечных сокращений (ЧСС) у больных: 95 130 83 115 120 1. Найдем среднее арифметическое значение выборки:
2. Вычислим дисперсию (рассеивание ряда). При вычислении дисперсии малой выборки сумму квадратов отклонений каждой варианты от средней арифметической величины делят не на объем выборки n, а на число n–1: D(x)=s2=
Число df=n–1 называют числом степеней свободы. Смысл этого параметра в данном случае можно объяснить следующим образом: если имеется вариационный ряд состоящий из n членов, и была определена средняя арифметическая величина (
3. Среднее квадратическое отклонение выборки: s= Мы определили так называемые точечные (т.е. выраженные одним значением) параметры малой выборки. Перейдем к оценке генеральной совокупности по нашей выборке. 4. Определим среднюю величину расхождения между параметрами выборки и генеральной совокупности. Эту величину называют средней квадратической ошибкой (или средней ошибкой, ошибкой выборочности, стандартной ошибкой) sx:
Из формулы видно, что размер определяемой стандартной ошибки зависит от среднего квадратического отклонения s выборочной совокупности и объема выборки n. Если обьекты отобраны в выборку случайным образом, то чем больше ее размеры, тем меньше стандартная ошибка, а значит, меньше расхождения в выборочной и генеральной совокупностях. Результат записывается в виде: ЧСС= Для определения доверительного интервала с заданной степенью вероятности, в котором находится значение генеральной средней, введем понятие критерия нормированного отклонения для распределения Стьюдента (критерий Стьюдента): t = Величиной нормированного отклонения t (по Стьюденту) является величина разности между средней арифметической выборки Из формулы (6) доверительный интервал для генеральной средней будет иметь вид:
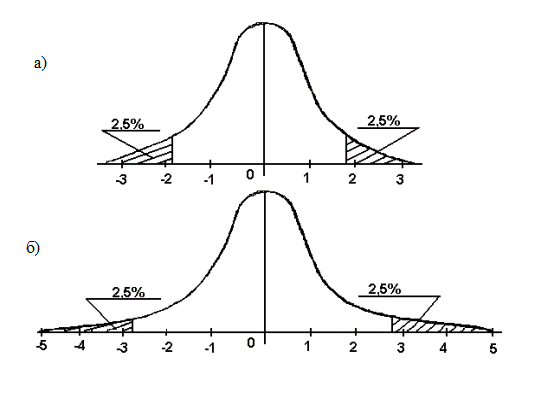
Оказалось, что распределение значений t отличается от нормального тем сильнее, чем меньше n (рис.1).
Рис.1. Разные значения t, отсекающие по 2,5% площади справа и слева: а) под кривой нормального распределения (n= б) под кривой t–распределения по Стьюденту (n=5, t=2,78).
Поэтому и вероятность нахождения выборочных средних в пределах определенных значений
Для числа опытов n=5 по таблицам Стьюдента t=2,78. Доверительный интервал:
По мере увеличения n, t – распределение Стьюдента приближается к нормальному. При n
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 , s2, s – соответствующие параметры выборки.
, s2, s – соответствующие параметры выборки. =108,6 (1)
=108,6 (1) =
= (2)
(2) 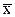 и остальные n–1 вариант. То есть имеется n–1 степени свободы. При числе опытов n больше либо равном 30 разница между n и n–1 не велика и не отражается на величине дисперсии.
и остальные n–1 вариант. То есть имеется n–1 степени свободы. При числе опытов n больше либо равном 30 разница между n и n–1 не велика и не отражается на величине дисперсии.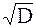 =
= 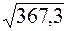 =19,16 (3)
=19,16 (3)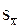 =
= 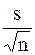
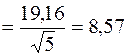 (4)
(4) (5)
(5) (6)
(6) (7)
(7)
 , t=1,96),
, t=1,96), t значительно снижается по сравнению с нормальным распределением. Так, для доверительной вероятности Р=0,95 значение t по таблицам для нормального закона распределения равно 1,96 и, следовательно, доверительный интервал:
t значительно снижается по сравнению с нормальным распределением. Так, для доверительной вероятности Р=0,95 значение t по таблицам для нормального закона распределения равно 1,96 и, следовательно, доверительный интервал: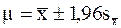 (n=
(n= 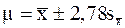 (n=5) (9)
(n=5) (9) 30 разница между ними практически исчезает. Таблицы t–критерия Стьюдента построены для заданных уровней доверительных вероятностей (уровней значимости) и числа степеней свободы: df=(n–1). Например, для числа опытов n=5 число степеней свободы равно 4. На пересечении df=4 и доверительной вероятности 0,95 (уровень значимости – 0,05) находим критерий Стьюдента – 2,78 (таблица 4 Приложения).
30 разница между ними практически исчезает. Таблицы t–критерия Стьюдента построены для заданных уровней доверительных вероятностей (уровней значимости) и числа степеней свободы: df=(n–1). Например, для числа опытов n=5 число степеней свободы равно 4. На пересечении df=4 и доверительной вероятности 0,95 (уровень значимости – 0,05) находим критерий Стьюдента – 2,78 (таблица 4 Приложения).


