
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 3. Свойства определителей. Обратная матрицаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§6. Свойства определителей §7. Обратная матрица Невырожденная и вырожденная матрицы Обратная матрица Необходимое и достаточное условие существования обратной матрицы Алгоритм вычисления обратной матрицы по формуле Вычисление обратной матрицы с помощью элементарных преобразований
§ 6. Свойства определителей
1. Если какая-либо строка (столбец) матрицы равны нулю, то ее определитель равен нулю.
Пример. Следствие 1. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен нулю. Следствие 2. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число, ее определитель умножится на это число. Замечание. За знак определителя можно выносить общий множитель какой-либо строки (столбца) в отличие от матрицы, за знак которой можно выносить лишь общий множитель всех элементов.
3. При транспонировании матрицы ее определитель не меняется. 4. При перестановке местами двух строк (столбцов) матрицы ее определитель меняет знак на противоположный. 5. Определитель матрицы не измениться, если к какой либо строке (столбцу) прибавить другую строку 9столбец), умноженную на число. 6. Определитель произведения двух квадратных матриц равен произведению их определителей, т.е.
Замечание. Даже если А ∙ В ≠ В ∙ А,
Итак, используя свойства определителей, можно всякий определитель свести к треугольному виду. Рассмотрим этот процесс на примере.
Пример. Вычислить определитель Решение.
§ 7. Обратная матрица
Для каждого числа а ¹ 0 существует обратное число а –1 такое, что а · а –1 = 1. Для квадратных матриц вводиться аналогичное понятие. Рассмотрим квадратную матрицу
Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля, и вырожденной если ее определитель равен нулю. Квадратная матрица А –1 называется обратной для квадратной матрицы А, если их произведение как слева, так и справа равное единичной матрице: А · А –1 = А –1· А = Е. В отличие от чисел, не каждая квадратная матрица имеет обратную. Теорема (необходимое и достаточное условие существования обратной матрицы). Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденная. Замечание. Если обратная матрица существует, то она единственна.
Обратная матрица может быть вычислена по формуле:
где Аij – алгебраические дополнения элементов матрицы А.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |


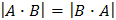 .
.

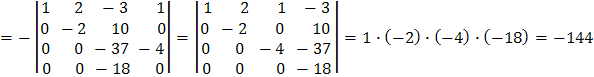
 .
.



