Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Действия над матрицами.Содержание книги Поиск на нашем сайте
Вопрос. Действия над матрицами. 1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B, т.е.
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц 6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами Пример
Вопрос. Ранг матрицы. Ранг матрицы представляет собой важную числовую характеристику. Наиболее характерной задачей, требующей нахождения ранга матрицы, является проверка совместности системы линейных алгебраических уравнений. В этой статье мы дадим понятие ранга матрицы и рассмотрим методы его нахождения. Для лучшего усвоения материала подробно разберем решения нескольких примеров. Навигация по странице. · Определение ранга матрицы и необходимые дополнительные понятия. · Нахождение ранга матрицы по определению. · Нахождение ранга матрицы методом окаймляющих миноров. · Нахождение ранга с помощью элементарных преобразований матрицы (методом Гаусса).
Нахождение ранга матрицы по определению.
Итак, первым методом нахождения ранга матрицы является метод перебора миноров. Этот способ основан на определении ранга матрицы. Пусть нам требуется найти ранг матрицы А порядка Вкратце опишем алгоритм решения этой задачи способом перебора миноров. Если есть хотя бы один элемент матрицы, отличный от нуля, то ранг матрицы как минимум равен единице (так как есть минор первого порядка, не равный нулю). Далее перебираем миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы равен единице. Если существует хотя бы один ненулевой минор второго порядка, то переходим к перебору миноров третьего порядка, а ранг матрицы как минимум равен двум. Аналогично, если все миноры третьего порядка равны нулю, то ранг матрицы равен двум. Если существует хотя бы один минор третьего порядка, отличный от нуля, то ранг матрицы как минимум равен трем, а мы преступаем к перебору миноров четвертого порядка.
И так далее. Отметим, что ранг матрицы не может превышать наименьшего из чисел p и n. Вопрос. Формулы для вычисления определителей второго и третьего порядков.
Вопрос. Чему равен определитель треугольной матрицы? Определитель треугольной матрицы равен произведению элементов на её главной диагонали. Вопрос. Что такое невырожденная матрица. Невырожденная матрица (иначе неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.
Вопрос. Решение матричных уравнений с помощью обратной матрицы. Обратная матрица Пусть имеется квадратная матрица n-го порядка
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка. Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают. Теорема условия существования обратной матрицы Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной. Матрица А = (А1, А2,...Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы Эквивалентные матрицы Пусть R и S два векторных пространства размерности n и m соответственно над числовым полем K, и пусть A линейный оператор отображающий R в S. Выясним, как меняется матрица оператора A при изменении базисов в пространствах R в S. Выберем произвольные базисы в пространствах R в S и обозначим через
соответствует матричное равенство
где х и у векторы x и y, представленные в виде координатных столбцов в базисах Выберем теперь в пространствах R и S другие базисы
Обозначим через Q и P невырожденные квадратные матрицы порядков n и m соответственно, которые осуществляют преобразование координат в пространствах R и S при переходе от старых базисов к новым (см.линейное пространство). Тогда связь между векторами в старых и новых базисах можно представить следующими равенствами:
Тогда, учитывая (3) и (4), имеем
Обозначив T=Q −1, и учитывая (3) и (5) получим:
Определение 1. Две прямоугольные матрицы A и B одинаковых размеров называются эквивалентными, если существуют две квадратные невырожденные матрицы P и T такие, что выполнено равенство
Отметим, что если A -матрица порядка m×n, то P и T квадратные матрицы порядков m и n, соответственно. Из (6) следует, что две матрицы, соответствующие одному и тому же линейному оператору A при различном выборе базисов в пространствах R и S эквивалентны между собой. Верно и обратное утверждение. Если матрица A соответствует оператору A, а матрица B эквивалентна матрице A, то она соответствует этому же линейному оператору A при других базисах в R и S. Выясним, при каких условиях две матрицы эквивалентны. Теорема. Для того, чтобы две матрицы одинаковых размеров были эквивалентны между собой, необходимо и достаточно, чтобы они имели один и тот же ранг. Доказательство. Необходимость. Так как умножение матрицы на квадратную невырожденную матрицу не может изменить ранг матрицы, то из (7) имеем:
Достаточность. Пусть задан линейный оператор A, отображающий пространство R в S и пусть этому оператору отвечает матрица A размера m×n в базисах
Зададим новый базис в пространстве R:
Тогда учитывая (8), имеем:
Далее выберем векторы
Дополним эти векторы некоторыми векторами Тогда матрица оператора A в новых базисах
где в матрице E ' -на главной диагонали стоят r единиц, а остальные элементы равны нулю. Так как матрицы A и E ' соответствуют одному и тому же оператору A, то они эквивалентны между собой. Выше мы показали, что эквивалентные матрицы имеют один и тот же ранг, следовательно ранг исходной матрицы A равен r. Из вышеуказанного следует, что произвольная m×n матрица ранга r эквивалентна матрице E ' - порядка m×n. Но E ' - однозначно определяется заданием размерности m×n матрицы и его ранга r. Следовательно все прямоугольные матрицы порядка m×n и ранга r эквивалентны одной и той же матрице E ' и, следовательно, эквивалентны между собой. Вопрос. Системы линейных алгебраических уравнений: основные понятия, виды Определение СЛАУ Определение Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Упорядоченный набор значений Пример Задание. Проверить, является ли набор Решение. Подставляем в каждое из уравнений системы
Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ. Ответ. Набор Виды систем Определение СЛАУ называется совместной, если она имеет, хотя бы одно решение. В противном случае система называется несовместной. Пример Система Пример Система Определение Система называется определённой, если она совместна и имеет единственное решение. В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой. Определение Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно. Пример
Определение Система называется квадратной, если количество уравнений равно количеству неизвестных. Пример Система Пример Задание. Систему Решение. Заданную СЛАУ записываем в матричной форме
вектор-столбец неизвестных:
вектор-столбец свободных коэффициентов:
то есть, запись СЛАУ в матричной форме:
Расширенная матрица системы Определение Расширенной матрицей системы Пример Задание. Записать матрицу и расширенную матрицу системы Решение. Матрица системы Замечание Если определитель системы равен нулю, то система может быть как совместной, так и несовместной. Замечание Данный метод удобно применять для маленьких систем с громоздкими вычислениями, а так же если нужно найти одну из неизвестных. Трудность заключается в том, что необходимо считать много определителей.
Примеры решения систем уравнений Пример Задание. Найти решение СЛАУ Решение. Вычисляем определитель матрицы системы:
Так как
Аналогично, определитель
Тогда получаем, что
Ответ. Пример Задание. При помощи формул Крамера найти решение системы Решение. Вычисляем определитель матрицы системы:
Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:
Таким образом,
Ответ.
Действия над векторами Определение Вектором называется направленный отрезок Суммой Свойства операции сложения: 1° 2° 3° 4° Определение Разностью Произведением 1. 2. 3. Свойства умножения вектора на число: 1° 2° 3° 4° 5° 6° 25 вопрос. Модуль (длина) вектора в координатной форме Если координаты вектора заданы, его длина находится по формуле
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами.
Определение Скалярным произведением двух ненулевых векторов
Свойства скалярного произведения: 1° 2° 3° Если 4° Если 5° 6° 7° Прямая линия в пространстве Определение 4. Пусть Пусть - произвольная декартова система координат, - произвольная прямая,
Уравнения (4.17) называются каноническими уравнениями прямой, проходящей через точку и имеющей в качестве направляющего вектор. Обозначим в (4.17) общее отношение через
Так как, то хотя бы одно из чисел Соотношения (4.18) при называются параметрическими уравнениями прямой, проходящей через точку и имеющей в качестве направляющего вектор. Замечание. Линию в пространстве естественно рассматривать как пересечение двух поверхностей, т.е. как совокупность точек, находящихся одновременно на двух поверхностях.
Если
определяет линию. Пусть: и:, не параллельна и не совпадает с ней. Тогда система уравнений
определяет линию пересечения и, т.е. прямую. Таким образом, система (4.20) – задание прямой как линии пересечения двух плоскостей и. Определение. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Примеры задач на вычисление расстояния от точки до прямой на плоскости Пример 1. Найти расстояние между прямой 3x + 4y - 6 = 0 и точкой M(-1, 3). Решение. Подставим в формулу коэффициенты прямой и координаты точки
Ответ: расстояние от точки до прямой равно 0.6. вопрос. Действия над матрицами. 1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B, т.е.
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц 6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами Пример
Вопрос. Ранг матрицы. Ранг матрицы представляет собой важную числовую характеристику. Наиболее характерной задачей, требующей нахождения ранга матрицы, является проверка совместности системы линейных алгебраических уравнений. В этой статье мы дадим понятие ранга матрицы и рассмотрим методы его нахождения. Для лучшего усвоения материала подробно разберем решения нескольких примеров. Навигация по странице. · Определение ранга матрицы и необходимые дополнительные понятия. · Нахождение ранга матрицы по определению. · Нахождение ранга матрицы методом окаймляющих миноров. · Нахождение ранга с помощью элементарных преобразований матрицы (методом Гаусса).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.217.247 (0.015 с.) |


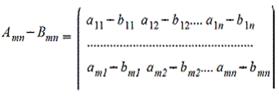






 .
.


 . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
. Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n. и
и  соответственно. Тогда (см. в линейные операторы) векторному равенству
соответственно. Тогда (см. в линейные операторы) векторному равенству и
и  . В новых базисах векторному равенству (1) будет соответствовать матричное равенство
. В новых базисах векторному равенству (1) будет соответствовать матричное равенство


 в качестве векторов базиса в S:
в качестве векторов базиса в S: до базиса в S.
до базиса в S.

 называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.
называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество. решением системы
решением системы 
 и
и  :
:

 является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов
является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов  это не выполняется.
это не выполняется.
 записать в матричной форме и выписать все матрицы, которые ей соответствуют.
записать в матричной форме и выписать все матрицы, которые ей соответствуют. , где матрица системы:
, где матрица системы:


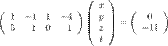
 называется матрица, полученная из матрицы системы
называется матрица, полученная из матрицы системы  , дописыванием справа после вертикальной черты столбца свободных членов.
, дописыванием справа после вертикальной черты столбца свободных членов.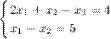
 , тогда расширенная матрица
, тогда расширенная матрица 
 при помощи метода Крамера.
при помощи метода Крамера.
 , то по теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель
, то по теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель  получим из определителя
получим из определителя  заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:
заменой его первого столбца столбцом свободных коэффициентов. Будем иметь: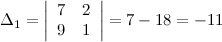
 получается из определителя матрицы системы
получается из определителя матрицы системы 

 ,
, 

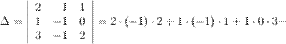


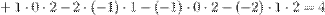








 , где точка
, где точка  - конец вектора.
- конец вектора. векторов
векторов  и
и  называют такой третий вектор
называют такой третий вектор  , начало которого совпадает с началом
, начало которого совпадает с началом 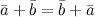 - коммутативность
- коммутативность - ассоциативность
- ассоциативность

 векторов
векторов  .
. вектора
вектора  называется вектор
называется вектор 

 , если
, если  ,
,  , если
, если  .
.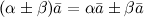
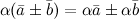


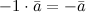




 - симметричность.
- симметричность. . Обозначается
. Обозначается 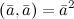 и называется скалярный квадрат.
и называется скалярный квадрат. , то
, то 
 и
и  , то
, то  . Верно и обратное утверждение.
. Верно и обратное утверждение.


 - произвольная прямая, любой вектор
- произвольная прямая, любой вектор  ,
, 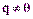 такой, что параллелен, называется направляющим вектором прямой.
такой, что параллелен, называется направляющим вектором прямой. ,
,  – направляющий вектор прямой. Этими условиями полностью определяется положение прямой в пространстве.
– направляющий вектор прямой. Этими условиями полностью определяется положение прямой в пространстве. коллинеарен
коллинеарен . (4.17)
. (4.17) , тогда
, тогда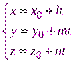 (4.18)
(4.18) ,
,  , либо отлично от нуля. Пусть для определенности
, либо отлично от нуля. Пусть для определенности  . Тогда при
. Тогда при  число
число  пробегает всю ось и
пробегает всю ось и  , и, таким образом,
, и, таким образом,  .
. и
и  - уравнения двух поверхностей, пересечением которых является линия, то система уравнений
- уравнения двух поверхностей, пересечением которых является линия, то система уравнений (4.19)
(4.19) (4.20)
(4.20)