Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V2: Линейные операции над матрицамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
I: S: Даны матрицы -: -: -: +: I: S: Дана матрица +: -: -: -: I: S: Если -: +: -: -: I: S: Даны матрицы -: -: -: +: I: S: Даны матрицы -: -: +: -: I: S: Даны матрицы -: -: -: +: I: S: Даны матрицы -: -: +: -: I: S: Если -: +: -: -: I: S: Если -: -: -: +: V2: Произведение матриц I: S: Для матриц А и В найдено произведение -: -: +: -: I: S: Операция произведения матриц правильно определена для матричного произведения вида … +: -: +: +: -: I: S: Операция произведения матриц правильно определена для матричного произведения вида … -: +: -: +: +: I: S: Операция произведения матриц правильно определена для матричного произведения вида … +: -: +: -: +: I: S: Операция произведения матриц правильно определена для матричного произведения вида … +: +: -: -: +: I: S: Операция произведения матриц правильно определена для матричного произведения вида … +: +: -: +: -: I: S: Заданы матрицы +: 3 -: −11 -: −7 -: 5 I: S: Дана матрица +: 5 -: – 5 -: – 1 -: 1 I: S: Элемент +: 3 I: S: Элемент +: 6 I: S: Элемент +: -1 I: S: Элемент +: 3 I: S: Заданы матрицы +: 3 -: − 11 -: − 7 -: 5 I: S: Дана матрица +: 5 -: – 5 -: – 1 -: 1 I: S:Если -: +: -: -: I: S: Если +: -: -: -: I: S:Если -: -: -: +: I: S:Если +: -: -: -: I: S: Дана матрица -: -: -: +: I: S: Дана матрица -: -: +: -: I: S: Дана матрица -: -: +: -: V2: Обратная матрица I: S: Матрица -: 0 +: 10 -: -10
-: 5 I: S: Матрица -: 3 -: 10 +: 9 -: -9 I: S: Матрица +: 10 -: 3 -: -10 -: 0 I: S: Для каких из матриц +: A -: B +: C -: D I: S: Для каких из матриц +: A -: B -: C +: D I: S: Для каких из матриц +: A +: B -: C -: D I: S: Матрица -: 3 -: 12 +: 0 -: – 12 I: S: Дана матрица +: -: -: -: I: S: Дана матрица +: -: -: -: V2: Системы линейных уравнений I: S: Если система линейных уравнений -: – 3 -: – 7 +: 6 -: 5 I: S: Если система линейных уравнений -: – 3 +: – 7 -: 6 -: 5 I: S: Система линейных уравнений -: – 3 -: 4 +: – 4 -: 3 I: S: Система линейных уравнений -: – 4 -: 2 +: – 2 -: 4 I: S: Система линейных уравнений -: 2 -: -5 +: -2 -: 5 I: S: Система линейных уравнений -: 6 -: -3 +: -6 -: 3 I: S: Если +: -: -: -: I: S: Дана система уравнений +: -: -: -: I: S: Дана система уравнений -: +: -: -: I: S: Система линейных уравнений L1: L2: L3: R1: 6 R2: 14 R3: – 4 R4: 2 I: S: Система линейных уравнений L1: L2: L3: R1: 23 R2: 11 R3: 5 R4: – 5 I: S: Система линейных уравнений L1: L2: L3: R1: 16 R2: 2 R3: 3 R4: – 3 I: S: Система линейных уравнений
L1: L2: L3: R1: 27 R2: 13 R3: – 3 R4: 3 I: S: Система линейных уравнений L1: L2: L3: R1: – 1 R2: 7 R3: 6 R4: – 6 I: S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса. -: -: -: +: I: S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса. -: +: -: -: I: S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса. -: -: +: -: I: S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей. L1: L2: L3: L4: R1: R2: R3: R4: R5: R6: I:
|
||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 620; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.166.217 (0.01 с.) |

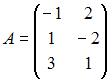 ,
,  ,
,  . Тогда матрица
. Тогда матрица  равна …
равна …



 . Если E – единичная матрица того же размера, что и матрица A, то матрица
. Если E – единичная матрица того же размера, что и матрица A, то матрица  равна …
равна …



 , то матрица
, то матрица  имеет вид...
имеет вид...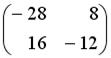



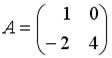 и
и  . Тогда
. Тогда  равно …
равно …



 ,
, 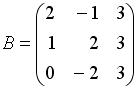 . Тогда матрица
. Тогда матрица 

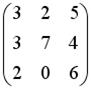

 ,
,  . Тогда матрица
. Тогда матрица 


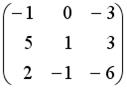
 ,
,  . Тогда матрица
. Тогда матрица 



 и
и  , то матрица
, то матрица  имеет вид…
имеет вид…


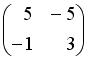
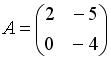 и
и  , то матрица
, то матрица  имеет вид…
имеет вид…



 , причем
, причем  . Тогда матрицей В может быть матрица …
. Тогда матрицей В может быть матрица …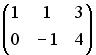




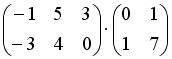






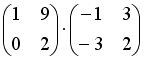
















 ,
,  . Тогда элемент
. Тогда элемент  матрицы
матрицы  равен …
равен …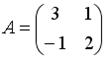 . Тогда элемент
. Тогда элемент  матрицы
матрицы 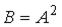 равен …
равен … в произведении матриц
в произведении матриц  равен …
равен … в произведении матриц
в произведении матриц  в произведении матриц
в произведении матриц  в произведении матриц
в произведении матриц  матрицы
матрицы 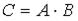 равен …
равен … . Тогда элемент
. Тогда элемент  матрицы
матрицы 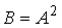 равен …
равен … ,
,  , тогда матрица
, тогда матрица 


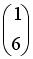
 ,
,  , тогда матрица
, тогда матрица 



 ,
,  , тогда матрица
, тогда матрица 


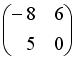
 ,
,  , тогда матрица
, тогда матрица 

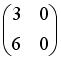

 . Тогда матрица
. Тогда матрица  имеет вид …
имеет вид …



 . Тогда матрица
. Тогда матрица  имеет вид …
имеет вид …

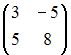

 . Тогда матрица
. Тогда матрица 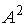 имеет вид …
имеет вид …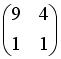



 не имеет обратной при k, равном …
не имеет обратной при k, равном … не имеет обратной при k, равном …
не имеет обратной при k, равном … не имеет обратной при k, равном …
не имеет обратной при k, равном …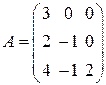 ,
,  ,
,  ,
,  существует обратная.
существует обратная. ,
,  ,
,  ,
,  существует обратная
существует обратная ,
,  ,
,  ,
,  не существует обратная
не существует обратная не имеет обратной, при
не имеет обратной, при  , равном …
, равном …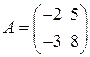 . Тогда обратная матрица
. Тогда обратная матрица  равна …
равна …



 . Тогда обратная матрица
. Тогда обратная матрица 
 где
где  ,
,  – некоторые числа, имеет бесконечное множество решений, то
– некоторые числа, имеет бесконечное множество решений, то  равно …
равно … где
где 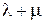 равно …
равно … не имеет решений, если
не имеет решений, если 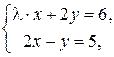 не имеет решений, если
не имеет решений, если  не имеет решений, если
не имеет решений, если  не имеет решений, если
не имеет решений, если 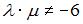 , то решение системы линейных уравнений
, то решение системы линейных уравнений  методом Крамера можно представить в виде …
методом Крамера можно представить в виде … ,
, 
 ,
, 
 ,
, 
 ,
, 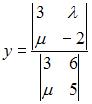
 . Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
. Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители… и
и 

 ,
,  и
и 
 . Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
. Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
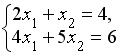 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.


 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями. решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями. решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями. решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.