
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
S: Укажите соответствие между уравнениями и видами кривых второго порядка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
L1: L2: L3: R1: парабола R2: гипербола R3: эллипс R4: окружность I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: эллипс R2: парабола R3: гипербола R4: окружность I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: парабола R2: окружность R3: гипербола R4: эллипс I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: окружность R2: парабола R3: эллипс R4: гипербола V2: Аналитическая геометрия в пространстве I: S: Нормальный вектор плоскости -: (7; 0; – 1) +: (7; – 1; – 1) -: (– 7; 1; 1) -: (7; 0; 0) I: S: Вектор -: 10 -: – 6 +: – 4 -: 6 I: S: Плоскости -: -: +: -: I: S: Координата -: 5 +: 3 -: 4 -: 2 I: S: Координата -: 7 -: 10 -: 13 +: 11 I: S: Координата -: 5 -: 3 -: 6 +: 4 I: S: Координата +: 2 -: 3 -: 4 -: 1 I: S: Координата -: 4 -: 1 -: 2 +: 3 I: S: Уравнение прямой, проходящей через точку -: -: -: +: I: S: Уравнение прямой, проходящей через точку +: -: -: -: I: S: Уравнение прямой, проходящей через точку -: -: -: +: I: S: Уравнение прямой, проходящей через точку -: -: -: +: I: S: Точкой пересечения плоскости -: -: -: +: V1: Комплексные числа V2: Комплексные числа и их представление. I: S: Модуль комплексного числа -: 2 -: 14 +: 10 -: I: S: Установите соответствие между комплексным числом и его модулем L1: L2: L3: L4: R1: 5 R2: 2 R3: 3 R4: 13 R5: 7 I: S: Аргумент комплексного числа -: +: -: 2 -: I: S: Установите соответствие между комплексным числом и его аргументом L1: L2: L3: R1: R2: R3: R4: I: S: Установите соответствие между комплексным числом и его аргументом L1: L2: L3: R1: R2: R3: R4: I: S: Установите соответствие между комплексным числом и его аргументом L1: L2: L3: R1: R3: R2: R4: I: S: Установите соответствие между комплексным числом и его аргументом L1: L2: L3: R1: R2: R3: R4: I: S: Комплексное число -: -: +: -: I: S: Задано комплексное число L1: L2: L3: R1: R2: R3: R4: R5: I: S: Тригонометрическая форма записи комплексного числа имеет вид: +: -: -: -: I: S: Показательная форма записи комплексного числа имеет вид: -: -: -: +: I: S: Алгебраическая форма записи комплексного числа имеет вид: -: -: +: -: I: S: Установите соответствие между формой записи комплексного числа и ее названием: L1: L2: L3: R1: тригонометрическая R2: алгебраическая R3: показательная R4: степенная V2: Операции над комплексными числами. I: S: Если -: -: -: +: I: S: Если +: -: -: -: I: S: Значение выражения -: +: -: -: I: S: Значение функции -: +: -: -: I: S: Значение функции -: -: -: +: I: S: Значение функции +: – 9 – 15i -: 15 – 15i -: – 9 – 9i -: 15 – 9i I: S: Значение функции -: – 9 – 15i -: 15 – 15i +: – 9 + 9i -: 15 – 9i I: S: Значение функции -: 40 + 13i +: – 32 + 25i -: – 32 + 13i -: 40 + 25i I: S: Значение функции -: 40 + 13i -: – 32 + 25i +: – 32 – 23i -: 40 + 25i I: S: Значение функции -: 4 – 8i -: – 6i +: – 8i -: 4 – 6i I: S: Значение функции -: 8i -: – 8i +: 0 -: 4 – 6i I: S: Если +: 16 -: 2 i -: 16 i -: 2 I: S: Если +: 0 -: -: -: V1: Элементы теории пределов V2: Понятие функции I: S: Пусть +: -: -: +: I: S: Пусть +: -: -: +: I: S: Пусть +: -: -: +: I: S: Пусть +: -: -: +: I: S: Пусть +: -: +: -: I: S: Областью определения функции +: -: -: -: I: S: Областью определения функции -: -: +: -: I: S: Областью определения функции -: +: -: -: I: S: Областью определения функции -: -: -: +: I: S: Областью определения функции -: -: +: -: I: S: Областью определения функции -: -: -: +: I: S: Областью определения функции +: -: -: -: I: S: Областью определения функции +: -: -: -: I: S: Областью определения функции -: -: -: +: I: S: Областью определения функции -: +: -: -: I: S: Областью определения функции -: -: +: -: I: S: Количество целых чисел, принадлежащих области определения функции +: 4 I: S: Количество целых чисел, принадлежащих области определения функции +: 4 I: S: Количество целых чисел, принадлежащих области определения функции +: 7 I: S: Количество целых чисел, принадлежащих области определения функции +: 2 I: S: Количество целых чисел, принадлежащих области определения функции +: 3
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.007 с.) |


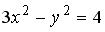






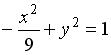


 имеет координаты…
имеет координаты…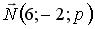 перпендикулярен плоскости
перпендикулярен плоскости  . Тогда значение p равно …
. Тогда значение p равно … и
и 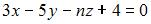 параллельны при значениях
параллельны при значениях 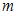 и
и  , равных …
, равных … ;
; 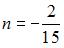
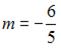 ;
; 

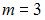 ;
; 
 точки
точки  , принадлежащей плоскости
, принадлежащей плоскости 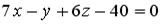 , равна…
, равна… точки
точки  , принадлежащей плоскости
, принадлежащей плоскости  , равна…
, равна…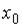 точки
точки  , принадлежащей плоскости
, принадлежащей плоскости  , равна…
, равна…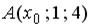 , принадлежащей плоскости
, принадлежащей плоскости  , равна…
, равна… , равна…
, равна…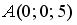 перпендикулярно плоскости
перпендикулярно плоскости 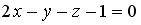 , имеет вид…
, имеет вид…

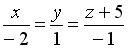

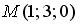 перпендикулярно плоскости
перпендикулярно плоскости  , имеет вид…
, имеет вид…
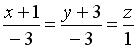

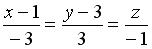
 перпендикулярно плоскости
перпендикулярно плоскости  , имеет вид…
, имеет вид…


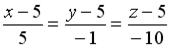
 перпендикулярно плоскости
перпендикулярно плоскости  , имеет вид…
, имеет вид…



 с осью
с осью  является …
является …



 равен …
равен …

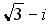


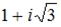 равен …
равен …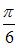
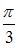
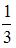

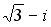




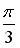
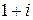





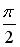




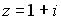
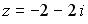
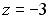
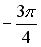


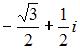 в тригонометрической форме имеет вид …
в тригонометрической форме имеет вид …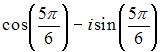


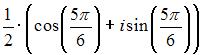
 . Установите соответствие:
. Установите соответствие:

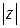








 – решение линейного уравнения
– решение линейного уравнения  , то
, то 



 и
и  , то выражение
, то выражение 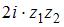 равно …
равно …


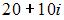
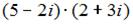 равно …
равно …


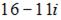
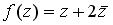 в точке
в точке  равно…
равно…



 равно…
равно… в точке
в точке 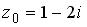 равно…
равно… равно…
равно…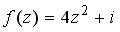 в точке
в точке  равно…
равно… равно…
равно…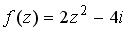 в точке
в точке  равно…
равно… равно…
равно… , то
, то  равно …
равно … , то сумма всех значений квадратного корня из
, то сумма всех значений квадратного корня из  равна …
равна …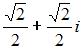


 . Тогда сложная функция
. Тогда сложная функция  нечетна, если функция
нечетна, если функция  задается формулами…
задается формулами…

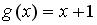




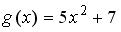



 . Тогда сложная функция
. Тогда сложная функция 


 является множество точек вида
является множество точек вида



 является множество точек вида
является множество точек вида

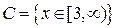

 является множество точек вида
является множество точек вида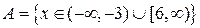


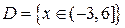
 является множество точек вида
является множество точек вида
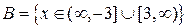

 является множество точек вида
является множество точек вида



 является множество точек вида
является множество точек вида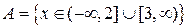



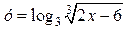 является множество точек вида
является множество точек вида



 является множество точек вида
является множество точек вида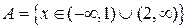


 является множество точек вида
является множество точек вида

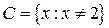

 является множество точек вида
является множество точек вида


 является множество точек вида
является множество точек вида



 равно …
равно … равно …
равно … равно …
равно … равно …
равно … равно …
равно …


