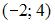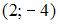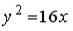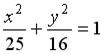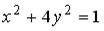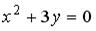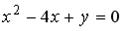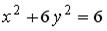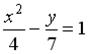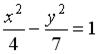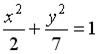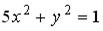Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
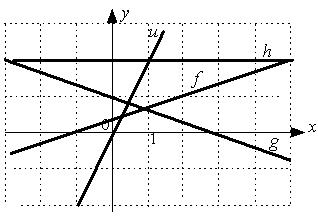
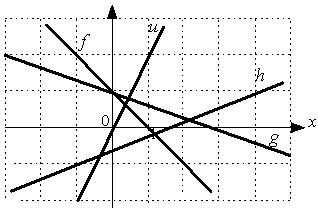
L1: L2: L3: L4: R1: R2: R3: R4: R5: R6: I: S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей. L1: L2: L3: L4: R1: R2: R3: R4: R5: R6: I: S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей. L1: L2: L3: L4: R1: R2: R3: R4: R5: R6: V2: Векторная алгебра I: S: Известны координаты точек -: +: -: -: I: S: Даны векторы -: -: +: -: I: S: Если известны координаты вершин +: -: -: -: I: S: Даны векторы -: -: +: -: I: S: Направляющим для прямой, заданной уравнением -: -: +: -: I: S: Если -: 9 +: 4 -: 14 -: 20 I: S: Даны векторы -: 35 -: 68.2 +: 191 -: 0 I: S: Площадь треугольника, образованного векторами -: -: +: -: I: S: Направляющий вектор прямой, заданной как пересечение двух плоскостей -: -: -: +: I: S: Длина стороны квадрата, площадь которого равна площади параллелограмма, построенного на векторах -: 1 -: +: -: 3 I: S: Векторное произведение векторов -: +: -: -: I: S: Векторное произведение векторов -: -: -: +: I: S: Векторное произведение векторов -: -: +: -: I: S: Векторное произведение векторов -: +: -: -: I: S: Векторное произведение векторов -: +: -: -: V1: Аналитическая геометрия V2: Прямая на плоскости I: S: Положительный угловой коэффициент имеют прямые:
-: h +: u +: f -: g I: S: Отрицательный угловой коэффициент имеют прямые:
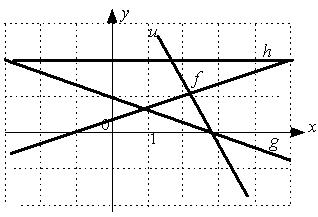
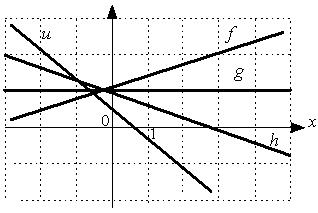
-: h +: u -: f +: g I: S: Положительный угловой коэффициент имеют прямые:
-: h -: g +: u +: f I: S: Укажите последовательность прямых в порядке убывания их угловых коэффициентов.
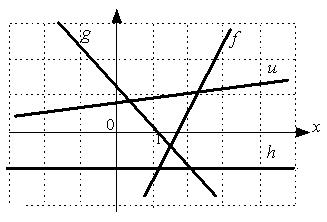
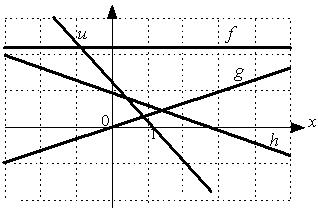
1: u 2: h 3: g 4: f I: S: Укажите последовательность прямых в порядке возрастания их угловых коэффициентов.
4: u 1: f 2: g 3: h I: S: Укажите последовательность прямых в порядке возрастания их угловых коэффициентов.
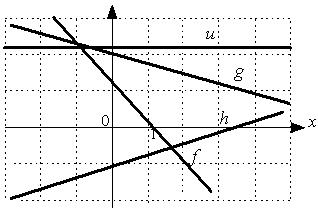
2: h 3: g 4: f 1: u I: S: Укажите последовательность этих прямых в порядке возрастания их угловых коэффициентов.
2: h 3: f 4: g 1: u I: S: Укажите последовательность этих прямых в порядке убывания их угловых коэффициентов.
3: g 4: f 1: h 2: u I: S: Расстояние от точки +: -: -: I: S: Расстояние от точки -: +: 7 -: -: 35 I: S: Острый угол между прямыми линиями -: +: -: -: I: S: Прямые +: 6 I: S: Прямые +: 6 I: S: Прямые +: -2 I: S: Прямые +: -1/2 I: S: Прямые +: -2 V2: Кривые второго порядка. I: S: Расстояние между фокусами эллипса +: 6 I: S: Расстояние между фокусами эллипса +: 16 I: S: Расстояние между фокусами гиперболы +: 26 I: S: Расстояние между фокусами гиперболы +: 40 I: S: Расстояние между фокусами гиперболы +: 50 I: S: Вещественная полуось гиперболы, заданной уравнением +: 3 I: S: Мнимая полуось гиперболы, заданной уравнением +: 2 I: S: Мнимая полуось гиперболы, заданной уравнением +: 4 I: S: Мнимая полуось гиперболы, заданной уравнением +:5 I: S: Большая полуось эллипса, заданного уравнением +: 5 I: S: Если прямая +: 2 I: S: Если прямая +: 3 I: S: Если прямая +: 2 I: S: Уравнение +: -: -: -: I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: Парабола R2: Эллипс R3: Гипербола R4: окружность I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: окружность R2: эллипс R3: парабола R4: гипербола I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: парабола R2: эллипс R3: окружность R4: гипербола I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: парабола R2: гипербола R3: эллипс R4: окружность I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: окружность R2: эллипс R3: парабола R4: гипербола I: S: Укажите соответствие между уравнениями и видами кривых второго порядка. L1: L2: L3: R1: парабола R2: окружность R3: гипербола R4: эллипс I:
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 738; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.222 (0.008 с.) |

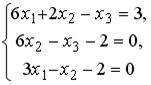

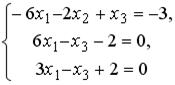
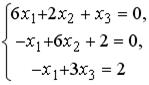

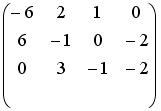




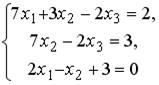
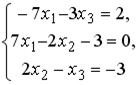

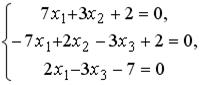





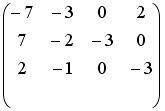
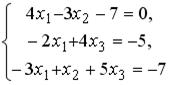

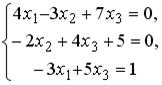




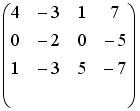


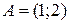 и
и 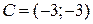 . Если
. Если 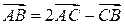 , то координаты точки
, то координаты точки 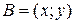 равны …
равны …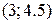

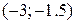
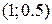
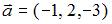 и
и 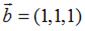 ; если
; если 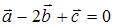 , то вектор
, то вектор 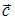 равен …
равен …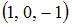
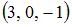

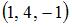
 ,
, 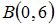 ,
, 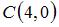 треугольника ABC, то вектор
треугольника ABC, то вектор 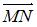 , где М и N – середины сторон АВ и ВС соответственно, равен …
, где М и N – середины сторон АВ и ВС соответственно, равен …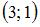
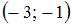
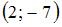
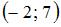
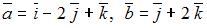 . Тогда линейная комбинация
. Тогда линейная комбинация 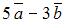 этих векторов равна …
этих векторов равна …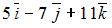


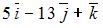
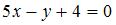 , будет вектор …
, будет вектор …



 ,
, 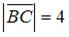 ,
, 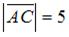 и точки A, B, C являются вершинами треугольника, то скалярное произведение векторов
и точки A, B, C являются вершинами треугольника, то скалярное произведение векторов 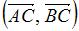 равно …
равно … и
и 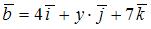 , где
, где 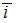 ,
, 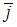 и
и 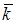 – ортонормированный базис. Известно, что скалярное произведение этих векторов равно 40, а угол между этими векторами равен
– ортонормированный базис. Известно, что скалярное произведение этих векторов равно 40, а угол между этими векторами равен 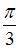 . Тогда значение
. Тогда значение 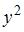 равно …
равно …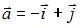 и
и  , равна …
, равна …
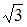
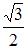
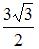
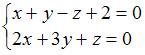 , равен …
, равен …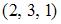
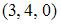
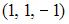
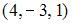
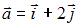 и
и 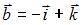 , равна …
, равна …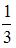
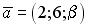 и
и  равно нулю, если…
равно нулю, если…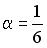 ;
; 
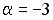 ;
; 
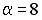 ;
; 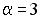 ;
;  и
и 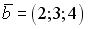 равно нулю, если…
равно нулю, если…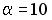 ;
; 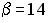
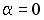 ;
; 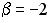
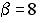
 ;
;  и
и  равно нулю, если…
равно нулю, если… ;
; 
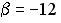
 ;
; 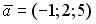 и
и 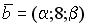 равно нулю, если…
равно нулю, если…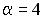 ;
; 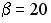
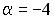 ;
; 
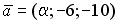 и
и 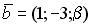 равно нулю, если…
равно нулю, если…


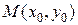 до прямой
до прямой 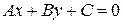 можно найти по формуле
можно найти по формуле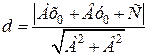
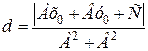
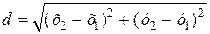
 до прямой
до прямой 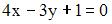 равно …
равно …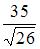

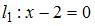 и
и 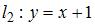 равен …
равен …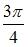
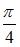
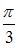
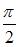
 и
и 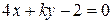 параллельны при
параллельны при 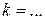
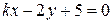 и
и 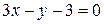 параллельны при
параллельны при 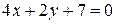 и
и  параллельны при
параллельны при  и
и 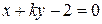 перпендикулярны при
перпендикулярны при  и
и 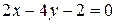 перпендикулярны при
перпендикулярны при 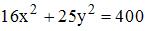 равно …
равно … равно …
равно … равно …
равно … равно …
равно …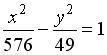 равно …
равно …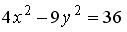 , равна…
, равна… , равна…
, равна…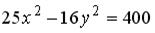 , равна…
, равна… , равна…
, равна… – уравнение асимптоты гиперболы
– уравнение асимптоты гиперболы 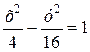 , то значение
, то значение 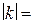 …
…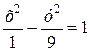 , то значение
, то значение 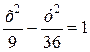 , то значение
, то значение 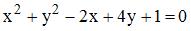 определяет окружность с центром в точке …
определяет окружность с центром в точке …