
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие свойства решений уравнений цепиСодержание книги
Поиск на нашем сайте
Как следует из примера 1.4, уравнения цепи представляют собой систему интегро-дифференциальных уравнений. При этом неизвестные токи – искомые реакции, их производные и интегралы входят в эти уравнения в первой степени. Это означает, что уравнения в системе – линейные. Линейные дифференциальные уравнения обладают следующими свойствами: 1. Умножение или деление правой и левой частей уравнения на любой множитель не изменяет равенства. Это означает, что изменение входного воздействия в k раз приводит к изменению реакции цепи в k раз, и наоборот. Это свойство позволяет в расчете линейной цепи вводить удобный масштаб для тока, напряжения и сопротивления.
2. Равенство не нарушается, если левую и правую части уравнения продифференцировать или проинтегрировать. Это свойство позволяет для упрощения решения входное воздействие (например, линейно-возрастающее) заменить его производной (постоянным) или интегралом. Затем полученный результат следует соответственно проинтегрировать или продифференцировать.
3. Сумма решений
Два важнейших следствия теоремы наложения в терминах теории цепей: 1) Искомое решение – ток или напряжение представляет собой совокупность двух решений: общего решения однородного уравнения (правая часть равна нулю) и частного, с правой частью отличной от нуля. Составляющую, обусловленную общим решением, называют свободной
где С течением времени Составляющую, представляющую собой частное решение называют принужденной или вынужденной. Вид ее определяется видом правой части уравнения, т. е. действующим на входе цепи источником – вынуждающей ²силы².
Определение частного решения в случае произвольной вынуждающей силы – сложная задача, которая будет рассмотрена в следующем разделе. 2) Действующий на входе цепи сигнал произвольной формы можно представить для упрощения анализа суммой элементарных составляющих. Эти составляющие могут быть постоянными, синусоидальными, экспоненциальными или иной формы. Если рассматриваются цепи с произвольными периодическими воздействиями, то в качестве элементарных составляющих следует выбирать синусоидальные, поскольку периодические функции легко раскладываются в тригонометрический ряд Фурье. При этом постоянная составляющая ряда Фурье может рассматриваться как синусоидальная составляющая нулевой частоты. Именно поэтому в следующем разделе изложение методов анализа ведется для цепей с сигналами гармонической (синусоидальной) формы.
ОСНОВНЫЕ МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕКИХ ЦЕПЕЙ
Вынужденные составляющие в виде постоянной величины и периодической синусоидальной функции времени (частное решение дифференциального уравнения) называют установившимися составляющими, поскольку они характеризуют установившийся режим цепи после затухания свободной составляющей. Режим перехода цепи от одного установившегося состояния к другому принято называть переходным процессом или режимом. Ниже рассматриваются методы расчета цепей в установившемся режиме.
КОМПЛЕКСНЫЙ МЕТОД
Токи и напряжения, изменяющиеся во времени по синусоидальному закону, записывают:
где
Число периодов в секунду называют циклической или просто частотой
Амплитуда, частота и начальная фаза полностью характеризуют синусоидально изменяющуюся величину, однако на практике для оценки действия синусоидальных токов и напряжений вводят действующее и среднее (по модулю) значения.
Действующим или среднеквадратичным называют величину:
На действующие значения градуируются приборы, предназначенные для измерения переменных токов и напряжений. Среднее значение по модулю определяется:
На средние значения градуируются приборы, предназначенные для измерения постоянных токов и напряжений. На рис. 2.1 показаны временной график синусоидальной функции (а) и ее векторное изображение или векторная диаграмма (б).
а б Рис. 2.1 Нетрудно представить, что операции с синусоидальными токами и напряжениями, имеющими различные начальные фазы, в тригонометрической и графической формах сложны и громоздки. Поэтому широкое распространение получил комплексный (символический) метод. Суть его - в представлении синусоидальных функций одинаковой частоты функциями комплексной частоты. Для перехода от функций времени к функциям комплексной частоты используют формулу Эйлера: Если ввести в рассмотрение знак соответствия При сложении (вычитании) комплексных чисел их записывают в алгебраической форме и отдельно складывают (вычитают) их действительные и мнимые части. Например, если а то где Умножение и деление комплексных величин производят, как правило, в показательной форме:
В комплексной форме дифференцирование по времени соответствует умножению, а интегрирование - делению комплексных значений рассматриваемых функций на jw, так что:
Величины XL и XC - индуктивное и емкостное сопротивления гармоническому току; Z L и Z C – соответственно индуктивное и емкостное сопротивления в комплексной форме. Для резистивного элемента напряжение в комплексной форме определяется: uR = R × i где Z R = R - величина вещественная. Если пользоваться действующими значениями, тогда: U R = Z R × I; U L = Z L × I; U C = Z C × I. Примеры определения входных (эквивалентных) комплексных сопротивлений двухполюсников, состоящих (образованных) из R, L, C – элементов приведены в табл. 2.1. Таблица 2.1
Величину, обратную комплексному сопротивлению, называют комплексной проводимостью Выражения комплексных сопротивления Z и проводимости Y для любого двухполюсника содержат информацию как о соотношении между действующими (амплитудными) значениями тока I и напряжения U, так и фазовом сдвиге между ними:
Вещественная и мнимая части комплексного сопротивления представляют его активное R и реактивное X сопротивления:
Аналогично вещественная и мнимая части комплексной проводимости Y представляют активную G и реактивную b проводимости:
Нетрудно установить, что
Соотношения между R, X, Z, G, b, y иногда изображают графически в виде треугольников сопротивлений и проводимостей, показанных на рис. 2.2, а и б соответственно.
а б Рис. 2.2 Согласно рис. 2.2, активные и реактивные сопротивления и проводимости без фазового множителя
ПРИМЕР 2.1. Определите комплексную амплитуду тока, изменяющегося по закону i(t) = 10sin(100t + 300).
РЕШЕНИЕ. Комплексная амплитуда представляет собой функцию, модуль которой равен амплитуде заданной функции времени, а фазовый множитель еjY определяется ее начальной фазой во временной области. Таким образом, I m = 10ej30 или в алгебраической форме I m = 8,65 + j5.
ПРИМЕР 2.2. Определить входные комплексные сопротивления цепи по рис. 2.3 с элементами R = 10 Ом; L = 50 мГн; С = 1 мФ на частотах w1 = 0 и w2 = 100 рад/с.
РЕШЕНИЕ. Сопротивления элементов цепи представляем в комплексной форме: Z R = R; Z L = jwL и Z C = Рис. 2.3
Подставляя численные значения параметров элементов для частоты w1 = 0, получаем:
Для частоты w2 = 100 рад/с имеем:
ЗАМЕЧАНИЯ. 1. Сигнал с частотой w1 = 0 и периодом Т = ¥ является постоянным во времени, поэтому входное сопротивление данной цепи чисто вещественное, соответствующее сопротивлению R. 2. Отсутствие мнимой составляющей в комплексном сопротивлении Z (100) на частоте w2 = 100 рад/с объясняется взаимной компенсацией сопротивлений индуктивности и емкости. Уравнения цепи в комплексной форме записывают на основе законов Кирхгофа, как показано в табл. 2.2. Для однозначности записи уравнений цепи соблюдают следующие правила: 1. Положительные направления напряжений ветвей совпадают с произвольно выбранными положительными направлениями токов; 2. При записи первого закона Кирхгофа токи, выходящие из узла, считаются положительными, а входящие в узел - отрицательными;
Таблица 2.2
3. При записи второго закона Кирхгофа положительным считают напряжение, направление которого совпадает с направлением обхода контура; 4. Положительные направления напряжения и тока на источниках энергии - противоположны. Например, для узла, изображенного на рис. 2.4, а, следует записать:
а б Рис. 2.4
если токи синусоидальные, одинаковой частоты. Для контура, показанного на рис. 2.4, б, имеем:
или Из первого закона Кирхгофа, в частности, следует:
Это дает возможность определять один из токов по m-1 известным. Аналогичное равенство записывается и для второго закона Кирхгофа:
ПРИМЕР 2.3. Определить ток i1 по рис. 2.4, а, если i2 = 3sinwt A; i3 = 4coswt A.
РЕШЕНИЕ. На основании первого закона Кирхгофа i1 = i2 - i3 = 3sinwt - 4coswt. Вычисления произведем комплексным методом, изобразив
тогда Переходя во временную область, получаем: i1 = 5sin(wt - 53,130) А.
ПРИМЕР 2.4. Определить действующие комплексные значения токов I 3, I 5 и I 6 для фрагмента цепи, показанного на рис. 2.5, по заданным токам, изменяющимся по синусоидальному закону:
Рис. 2.5
РЕШЕНИЕ. Нетрудно показать, что первый закон Кирхгофа применим не только к узлу, но и к любому сечению, поэтому - i1 - i2 + i3 = 0. Отсюда i3 = i1 + i2. Затем i5 = i3 + i4 и i6 = - i2 - i4. Записывая заданные токи в комплексной форме для действующих значений
ПРИМЕР 2.5. Определите в комплексной форме действующее значение напряжения ветви по рис. 2.6, если R = 86,5 Ом; XL = 20 Ом; XC = 150 Ом;
Рис. 2.6 РЕШЕНИЕ. Согласно второму закону Кирхгофа для действующих значений напряжений имеем:
или где Подставляя численные значения, получаем:
МЕТОД НАЛОЖЕНИЯ
В основе метода наложения лежит принцип наложения, согласно которому исходная цепь представляется совокупностью подсхем (по числу источников). В каждой подсхеме оставляют только один из источников, замыкая накоротко зажимы всех остальных источников ЭДС и размыкая ветви с источниками тока. Рис. 2.7 иллюстрирует сказанное.
Рис. 2.7
Искомый ток находится алгебраическим суммированием токов подсхем:
Метод наложения прост и нагляден, однако применим к расчету цепей с малым числом источников. Расчет подсхем производят, как правило, преобразованием, определяя эквивалентное сопротивление относительно зажимов источника и используя затем закон Ома. Основные преобразования приведены в табл. 2.1 и на рис. 2.8.
Рис. 2.8 Взаимное соответствие сопротивлений ²звезды² и ²треугольника² устанавливается по уравнениям (2.1):
ПРИМЕР 2.6. В цепи гармонического тока по рис. 2.9, а с известными сопротивлениями
б в Рис. 2.9 РЕШЕНИЕ. Согласно принципу наложения, искомый ток представляем суммой частичных токов от каждого из источников, действующих независимо друг от друга. Иными словами, расчет токов ветвей произведем по частным схемам (подсхемам), в каждой из которых действует только один независимый источник. Для заданной схемы имеем две подсхемы В подсхеме по рис. 2.9, б:
Ветвь с источником тока в этой схеме разомкнута, поскольку внутреннее сопротивление идеального источника тока бесконечно велико. В подсхеме по рис. 2.9, в сопротивление Z 1 замкнуто накоротко, поскольку внутреннее сопротивление идеального источника ЭДС равно нулю. Искомый ток I J найдем по правилу п а р а л л е л ь н ы х ветвей (разброса):
Подставляя численные значения, имеем:
И, наконец, искомый ток
ЗАМЕЧАНИЕ. Правильность расчета контролируется подсчетом баланса мощностей - равенства мощностей, выработанных источниками энергии, и мощностей, потребленных элементами цепи (нагрузкой):
где
Р - активная мощность цепи; Q - реактивная.
МЕТОД КОНТУРНЫХ ТОКОВ Максвелл предложил при расчете цепей в качестве независимых переменных принимать токи, названные контурными, ²замыкающиеся² по главным контурам (см. рис. 2.10). Поскольку каждый такой ток, проходя узел, втекает в него и вытекает, необходимость записывать уравнения по первому закону Кирхгофа отпадает. Ток ветвей, по которым проходит только один контурный ток, равен соответствующему контурному току. Токи смежных ветвей, по которым замыкается несколько контурных токов, равны их алгебраической сумме.
Рис. 2.10 Для каждого независимого контура, исключая контуры с источниками тока, по второму закону Кирхгофа записывают уравнения в форме:
Здесь k - номер рассматриваемого контура; i - нумерация контуров с контурными токами Ji (i = 1, 2,...., n); j - нумерация вспомогательных контуров, содержащих ветви с ис- точниками тока Jj;
сопротивлениями связи. Если контурные токи по сопротивлению связи проходят в противоположных направлениях, оно считается отрицательным;
сопротивлений k – контура;
турной ЭДС;
сопротивлениях связи ЭДС, входящие в контур k, берутся со знаком ²плюс², если их направления совпадают с направлением контурного тока J k, и со знаком ²минус² - в противном случае. Произведение Для контурного тока J 1 по рис. 2.10 согласно (2.2), следует записать:
Если один из контурных токов был бы током источника тока, его следовало бы записать в правой части уравнения.
Правила записи контурных уравнений 1. Ток рассматриваемого контура умножается на собственное контурное сопротивление. 2. К данному произведению дописываются произведения всех других контурных токов на сопротивления связи с учетом знака сопротивлений связи. 3. В правой части записывают контурную ЭДС и напряжения, вызванные токами источников тока.
ПРИМЕР 2.7. В цепи по рис. 2.11 с известными сопротивлениями R1 = R3 = R4 = R5 = 1 Ом и R2 = 2 Ом и постоянными во времени источниками ЭДС E1 = 10 В, Е2 = 4 В и тока J = 2 A определить токи ветвей I1, I2, I3 методом контурных токов.
Рис. 2.11 РЕШЕНИЕ. За неизвестные в методе контурных токов принимают токи, замыкающиеся по главным (независимым) контурам. Для заданной схемы их три, причем один из токов - ток источника тока J - известен. Для токов J1, J2 составляем уравнения согласно (2.2):
Подставляя числовые значения, имеем:
Решая относительно J1 и J2, находим: J1 = 5 A, J2 = - 4 A. Токи в ветвях: I1 = J1 = 5 A, I2 = - J1 - J2 = - 5 + 4 = -1 A, I3 = - J2 = 4 A.
ЗАМЕЧАНИЯ. 1. Если контурные токи (планарных схем) замыкать по ячейкам с одинаковым направлением, то сопротивления связи будут отрицательными. 2. Не рекомендуется по ветви с источником тока замыкать другие контурные токи. 3. Определитель системы уравнений для цепи без управляемых источников при любых выбранных направлениях симметричен относительно главной диагонали. Это доказывает теорему взаимности, согласно которой при изменении направления передачи сигнала (перестановкой источника из одной ветви в другую) новый выходной сигнал получается равным прежнему. Цепи, удовлетворяющие теореме взаимности, называют обратимыми.
ПРИМЕР 2.8. Рассчитать токи ветвей схемы по рис. 2.12, а, полагая параметры элементов и коэффициенты управления k, a заданными.
а б Рис. 2.12 РЕШЕНИЕ. 1. Строим дерево графа, дополняем его хордами и определяем по ним главные контуры и положительные направления их обхода (рис. 2.12, б). 2. Записываем систему контурных уравнений для неизвестных контурных токов
3. Управляющие величины зависимых источников энергии выражаем через искомые контурные токи и подставляем в контурные уравнения:
4. Группируем слагаемые с контурными токами и получаем:
5. Токи ветвей выражаем через контурные токи:
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.17 (0.011 с.) |

 дифференциального уравнения для различных правых частей
дифференциального уравнения для различных правых частей  ,
,  является решением этого уравнения с правой частью:
является решением этого уравнения с правой частью:  . Согласно этому свойству (теорема наложения), реакция цепи на действие нескольких источников равна сумме реакции на действие каждого из отдельно взятых источников. Это один из основополагающих принципов теории линейных цепей, известный как принцип (теорема) наложения.
. Согласно этому свойству (теорема наложения), реакция цепи на действие нескольких источников равна сумме реакции на действие каждого из отдельно взятых источников. Это один из основополагающих принципов теории линейных цепей, известный как принцип (теорема) наложения. , поскольку цепь свободна от внешнего воздействия (отсутствие правой части соответствует короткому замыканию входных зажимов). Свободная составляющая определяется параметрами цепи и энергией, запасенной накопителями энергии: конденсатором и катушкой индуктивности. В общем виде ее решение записывается:
, поскольку цепь свободна от внешнего воздействия (отсутствие правой части соответствует короткому замыканию входных зажимов). Свободная составляющая определяется параметрами цепи и энергией, запасенной накопителями энергии: конденсатором и катушкой индуктивности. В общем виде ее решение записывается: ,
, - корни характеристического уравнения.
- корни характеристического уравнения. исчезает, поскольку
исчезает, поскольку  ,
,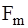 - амплитуда или максимальное значение,
- амплитуда или максимальное значение, ) – фаза, измеряемая в радианах или градусах,
) – фаза, измеряемая в радианах или градусах,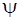 - начальная фаза, определяющая значение функции при t = 0,
- начальная фаза, определяющая значение функции при t = 0, - угловая частота (рад/с), определяющая период колебаний
- угловая частота (рад/с), определяющая период колебаний .
.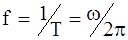 , измеряемой в герцах (Гц).
, измеряемой в герцах (Гц). .
. .
.
 , где
, где  - мнимая единица (йот). Согласно этой формуле,
- мнимая единица (йот). Согласно этой формуле,  , где
, где  обозначает мнимую часть комплексного числа, которое, в свою очередь, можно представить
обозначает мнимую часть комплексного числа, которое, в свою очередь, можно представить  . Здесь
. Здесь  - фазовый множитель, а
- фазовый множитель, а  - временной множитель.
- временной множитель. , то для фиксированного момента времени t = 0 будем иметь: f(t)
, то для фиксированного момента времени t = 0 будем иметь: f(t) 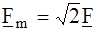 . Здесь
. Здесь  - комплексная амплитуда;
- комплексная амплитуда;  - комплексное действующее значение функции.
- комплексное действующее значение функции. ,
, ,
, ,
, ;
;  .
. ;
; .
.

 ;
;
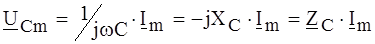 .
.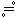 U mR = R × I m = Z R × I m ,
U mR = R × I m = Z R × I m ,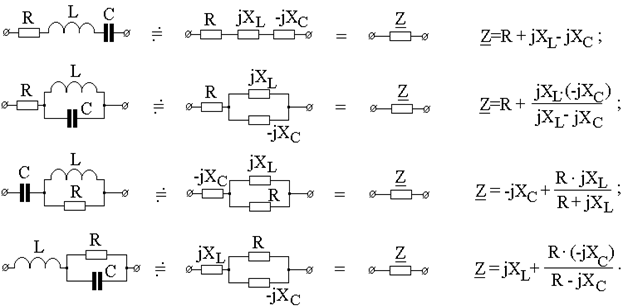

 . Как следует из приведенной табл. 2.1, при последовательном соединении пассивных элементов суммируются алгебраически их комплексные сопротивления, а при параллельном – комплексные проводимости.
. Как следует из приведенной табл. 2.1, при последовательном соединении пассивных элементов суммируются алгебраически их комплексные сопротивления, а при параллельном – комплексные проводимости.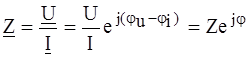 ;
;  .
. .
. .
. ;
; 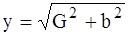 ;
;  .
.
 складывать н е л ь з я.
складывать н е л ь з я.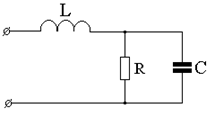
 . Эквивалентное комплексное сопротивление по отношению к входным зажимам:
. Эквивалентное комплексное сопротивление по отношению к входным зажимам: .
.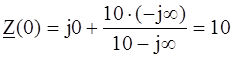 Ом.
Ом.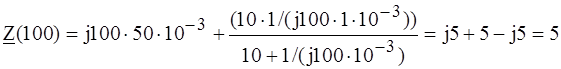 Ом.
Ом.




 или
или 
 ,
,
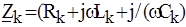 или
или


 или
или  ,
, .
. .
. .
. .
.
 ;
; 
 ;
; 
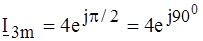 ,
, .
. А;
А;  А;
А; А.
А.
 ;
;  ;
;  ;
;  и подставляя их в уравнения, составленные по первому закону Кирхгофа, находим:
и подставляя их в уравнения, составленные по первому закону Кирхгофа, находим: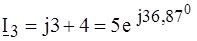 А;
А;  А;
А; А.
А. В;
В;  А.
А.
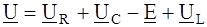
 ,
, А;
А;  В.
В. В.
В.
 .
.
 ;
;  ;
; ;
;  ; (2.1)
; (2.1) ;
;  .
. кОм;
кОм; 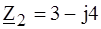 кОм и источниками ЭДС
кОм и источниками ЭДС  В и тока
В и тока  мА определить комплексное действующее значение тока
мА определить комплексное действующее значение тока  методом наложения.
методом наложения.
 .
. А.
А. .
. А.
А. А.
А. ,
, ;
; ,
, - сопряженное комплексное значение тока через i источник;
- сопряженное комплексное значение тока через i источник;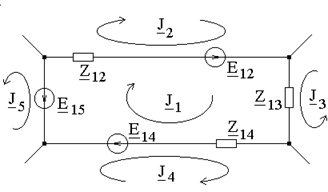
 (2.2)
(2.2) - сопротивления, входящие в k - и i - контуры, названные
- сопротивления, входящие в k - и i - контуры, названные - собственное контурное сопротивление, равное сумме
- собственное контурное сопротивление, равное сумме - алгебраическая сумма ЭДС в k - контуре, названная кон-
- алгебраическая сумма ЭДС в k - контуре, названная кон- - напряжения, вызванные токами источников тока на
- напряжения, вызванные токами источников тока на .
. .
.
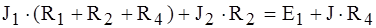 ;
; .
. ;
;  .
.
 и
и  (ток
(ток  полагаем известным):
полагаем известным):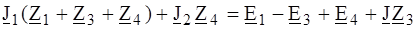 ;
; .
. ;
;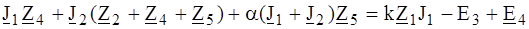 .
.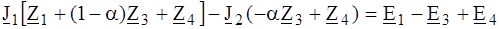 ;
; .
. ;
;  ;
;  ;
; ;
;  .
.


