
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Элементы и топологические свойстваСодержание книги
Поиск на нашем сайте
А. М. Купцов
ОСНОВЫ ТЕОРИИ ЦЕПЕЙ ЧАСТЬ 1
Линейные электрические цепи
Учебное пособие
Томск 1999
УДК 621.3.01(075) Купцов А. М.. Основы теории цепей. Часть 1. Линейные электрические цепи: Учебное пособие. - Томск: Изд. ТПУ, 1999. - 132 с.
Представлены основные разделы первой части курса ²Основы теории цепей². Материал иллюстрирован большим количеством примеров расчета и анализа электрических цепей в установившемся режиме. Большое внимание уделено электрическим цепям с управляемыми источниками. Пособие подготовлено на кафедре теоретических основ электротехники и предназначено для самостоятельной работы студентов электротехнических специальностей и направлений.
Печатается по постановлению Редакционно-издательского Совета Томского политехнического университета.
Рецензенты:
В. М. Дмитриев - проф., доктор техн. наук, зав. кафедрой теоретических основ электротехники Томского университета систем управления.
Кафедра теоретических основ электротехники Новосибирской академии водного транспорта.
Темплан 1999
© Томский политехнический университет, 1999
Электротехника - отрасль науки и техники, связанная с производством, распределением и практическим использованием электрической энергии. Роль и значение электрической энергии - общеизвестны: электричество является основой развития всего народного хозяйства, включая химическую промышленность, транспорт, сельское хозяйство и даже космос. Только на базе электричества оказалось возможным бурное развитие новейших направлений в автоматике, телемеханике, радиотехнике, технике связи, а также разработка и внедрение нескольких поколений ЭВМ. Широкое и разнообразное использование электрической энергии объясняется ее огромными преимуществами перед другими видами энергии: электрическая энергия сравнительно легко генерируется, транспортируется и преобразуется в другие виды энергии. Единственный ее недостаток - в сложности хранения (аккумулирования). История электротехники начинается с начала XIX столетия, когда Александр Вольта изобрел первый источник электрической энергии - гальванический элемент - вольтов столб (1802 г.).
Изобретение Вольта привело к всплеску научных исследований электрический явлений во всем мире, в том числе и в России. В. В. Петров в 1802 году, экспериментируя с батареей гальванических элементов, получил электрическую дугу и предсказал ее практическое применение для освещения и плавки металлов. В 1821 году М. Фарадей осуществил вращение проводника с током вокруг магнита, создав действующую модель электрического двигателя. Позднее (1831 г.) им был открыт закон электромагнитной индукции, составляющий вместе с законами Ома (1827 г.), Джоуля-Ленца (1844 г.) и Кирхгофа (1845 г.) основу современной теории электрических цепей. Первыми наиболее важными результатами практического использования электрической энергии были: 1832 г. – первый в мире электромагнитный телеграф, построенный в России П. Л.Шиллингом; 1839 г. – электромагнитный двигатель моторной лодки, испытанный русским ученым Якоби Б. С.; 1873 г. – лампа накаливания Лодыгина А. И.; 1876 г. – электрическая свеча и трансформатор Яблочкова П. Н.; 1882 г. – пуск в эксплуатацию первой в мире электростанции общественного пользования; 1889 – 1891 г. г. – разработка и применение трехфазной системы (двигатель, трансформатор, генератор) русским инженером М. О. Доливо – Добровольским; 1897 г. – создание радиосвязи А. С. Поповым. Формирование учебной дисциплины ²Электротехника² относится к началу XX века, когда профессор В. Ф. Миткевич в Петербургском политехническом институте начал читать курс ²Теория электрических и магнитных явлений², а профессор К. А. Круг в Московском высшем техническом училище – курс ²Теория переменных токов². В 1916 году К. А. Кругом издана первая книга по электротехнике ²Основы электротехники², ставшая настольной книгой инженеров-электриков. В последующие годы курс электротехники, развиваясь, претерпевал различные изменения. Из него выделялись специальные курсы, такие, как ²Основы радиотехники², ²Основы теории связи², ²Теория электрических машин², ²Электроника² и многие другие. В настоящее время студенты электроэнергетических направлений и специальностей изучают курс ²Теоретические основы электротехники² (ТОЭ), который состоит из двух частей - ²Теория электрических и магнитных цепей² и ²Теория электромагнитного поля².
Студенты направлений ²Автоматизация и управление², ²Приборостроение² и родственных им специальностей изучают курс ²Электротехника², основу которого составляет теория электрических цепей. Без глубоких и прочных знаний теории электрических цепей невозможно эксплуатировать, совершенствовать и разрабатывать новые устройства автоматики, радиотехники, электросвязи и электроэнергетики. Курсы ²ТОЭ² и ²Электротехника² - базовые дисциплины для вышеуказанных направлений и специальностей. ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Реальные элементы электрической цепи – сложные устройства, имеющие в общем случае нелинейные характеристики – зависимости: u(i) - для резистора; y(i) – для катушки индуктивности; q(u) – для конденсатора; u(i) или i(u) – для источников энергии. Однако во многих случаях их нелинейностью можно пренебречь. В этом случае говорят о линейной цепи. Электрическая цепь, имеющая в своем составе хотя бы один нелинейный элемент, будет нелинейной. Ниже будут рассмотрены линейные цепи. Исследование любой цепи начинают с построения ее модели, в которой для отображения свойств реальной цепи вводят в рассмотрение идеальные схемные элементы: активные и пассивные. К активным относят элементы, осуществляющие преобразование других видов энергии в электромагнитную, т. е. источники (генераторы); к пассивным – элементы, потребляющие или накапливающие электромагнитную энергию. П а с с и в н ы м и схемными элементами являются: р е з и с т и в - н ы й, учитывающий необратимые преобразования электрической энергии в механическую, химическую и другие виды; и н д у к т и в н ы й, учитывающий накопление энергии в магнитном поле; е м к о с т н ы й, учитывающий накопление энергии в электрическом поле. Для всех пассивных элементов энергия Линейные элементы полностью определяются постоянными параметрами: электрическим сопротивлением Взаимосвязи между напряжениями и токами, а также энергетические характеристики линейных идеальных пассивных элементов представлены в табл. 1.1. Таблица 1.1
ЗАМЕЧАНИЯ. 1. Использование понятий электрический ток и электрическое напряжение требует указания направлений их действия (выбираются произвольно). При согласованных (одинаковых) направлениях, как правило, указывают только направление тока (стрелкой). 2. Если в момент времени t = 0, принятый за начало рассмотрения процесса, ток индуктивного и напряжение емкостного элементов не равны нулю, то их значения суммируются с результатами интегрирования, т.е.
3. Зависимости, уравнения и элементы, обладающие формальным сходством, называют дуальными. Согласно табл. 1.1, дуальными являются R и G, L и C, UL и iC и т. д.
Пример 1.1. Определить закон изменения напряжений uR, uL, и uC на пассивных элементах цепи по рис. 1.1, полагая, что с момента времени t = 0 ток в них изменяется по закону i(t) = 2sinwt А, где w - круговая частота, равная 100 рад/с.
uR = i × R = 2sin100t B; на индуктивном элементе
на емкостном элементе
где ЗАМЕЧАНИЯ. 1. Ток синусоидальной формы вызывает на R, L, C - элементах напряжения той же формы, однако напряжение на резистивном элементе совпадает по фазе с током, на индуктивном - опережает, а на емкостном - отстает от тока на 900. 2. Индуктивный и емкостный элементы оказывают синусоидальному току сопротивление, зависящее от частоты. Сопротивление индуктивного элемента
ПРИМЕР 1.2. Определить закон изменения тока в пассивных элементах цепи с параметрами R = 1 Ом, L = 1 Гн, С = 0,1 Ф, подключенных к напряжению заданной формы (рис. 1.2, б, в, г, д). РЕШЕНИЕ. Заданное на рис.1.2, а напряжение представляем в аналитической форме:
Ток резистивного элемента полностью повторяет форму приложенного напряжения, согласно закону Ома Ток индуктивного элемента (рис. 1.2, г) определяется интегрированием приложенного напряжения:
Закон изменения тока в емкостном элементе определяется производной от приложенного напряжения, что дает:
График изменения этого тока представлен на рис. 1.2, д. А к т и в н ы е с х е м н ы е э л е м е н т ы, представляющие собой идеализированные источники энергии, как и реальные источники, делят на два типа: источники ЭДС и источники тока. Те и другие могут быть независимыми (просто источники) и зависимыми (управляемыми). Для источников энергии
Независимый источник ЭДС – двухполюсный элемент, напряжение на зажимах которого не зависит от проходящего через него тока и задано в любой момент времени. Напряжение на зажимах такого источника равно его ЭДС, направление которой указывается на схеме стрелкой (рис. 1.3, а). Если источник постоянной ЭДС (e(t) = E = const), то его внешняя характеристика – зависимость напряжения на его зажимах от отдаваемого тока – прямая линия (рис. 1.3, б). а б в г Рис. 1.3
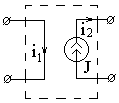
Независимый источник тока – двухполюсник, ток которого не зависит от напряжения на его зажимах. Условное изображение источника тока и его внешняя характеристика для J(t) = J = const показаны на рис. 1.3, в и 1.3, г.
Теоретически идеализированные источники обладают неограниченной мощностью, при этом внутреннее сопротивление у источника ЭДС и проводимость у источника тока равны нулю.
З а в и с и м ы м и (управляемыми) источниками называют источники, ЭДС или токи которых зависят от напряжения или тока на некотором участке цепи. Зависимые источники необходимы для отображения свойств электронных устройств: электронной лампы, транзистора, микросхемы и т. д.
Условные графические изображения зависимых источников приведены в табл. 1.2.
Таблица 1.2
Рис. 1.5 Внешняя характеристика источника согласно выбранным моделям, может быть представлена:
Для источника постоянной ЭДС (e(t) = E) внешняя характеристика показана на рис. 1.6, в, где Локальные модели наиболее распространенных электронных приборов, включающие в себя идеальные зависимые источники (табл. 1.2), будут рассмотрены в разделах 4.5.2 и 4.5.3.
Рис. 1.6
Для последовательного соединения:
где учтено, что ток течет от точки высшего потенциала к точке низшего потенциала, а направление действия источников ЭДС – противоположное (поэтому В общем случае Для параллельного соединения:
На рис. 1.7 для примера представлены схемы простой (а) и сложной (б) цепей.
а б Рис. 1.7 Структура любой цепи характеризуется такими понятиями, как узел, ветвь и контур. У з е л ц е п и – место соединения трех и более элементов, обозначенное на схеме точкой, как показано на рис. 1.7, причем для удобства изображения один и тот же узел может быть отмечен несколькими точками (рис. 1.7, а). В е т в ь ц е п и – элемент или группа последовательно соединенных элементов, включенных между двумя любыми узлами. На рис. 1.7, а четыре ветви, а рис. 1.7, б – шесть. К о н т у р ц е п и – любой замкнутый путь для тока, проходящий по нескольким ветвям. На рис. 1.7 пунктиром показано по одному из контуров.
Рис. 1.8 Если на ветвях графа изображены стрелки, указывающие направления токов ветвей, граф называют направленным. В противном случае граф – ненаправленный. При описании графов цепей используются те же понятия: узел, ветвь, контур, а также: дерево графа, хорда, сечение. При этом в теории графов ветвью часто считается каждый отдельно взятый элемент, так что узел – место соединения двух и более ветвей. Положительным направлением ветвей считается направление от узла. Д е р е в о г р а ф а – часть графа, включающая все узлы графа, не имеющая ни одного контура. На рис. 1.8, а дерево образовано одной ветвью, а на рис. 1.8, б – тремя, показанными сплошными линиями. Очевидно, что дерево графа содержит q – 1 ветвь, где q – число узлов. При этом любой граф содержит несколько деревьев.
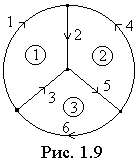
Х о р д ы или в е т в и с в я з и – ветви, не вошедшие в выбранное дерево. На рис. 1.8 – это пунктирные линии. С е ч е н и е г р а ф а – набор ветвей, удаление которых делит граф (схему) на две изолированные части (подграфы). Для анализа цепей значение имеют не все сечения и не все контуры, а только главные. Г л а в н о е с е ч е н и е – сечение, состоящее из ветвей связи и только одной ветви дерева. На рис. 1.8 главное сечение показано замкнутыми линиями со стрелками, указывающими положительное направление сечения, совпадающее с направлением ветви дерева. Число главных сечений равно число ветвей дерева, т. е. (q – 1). Г л а в н ы м называют контур, состоящий из ветвей дерева и только одной ветви связи (хорды). Направление контура определяется направлением входящей в него хорды. Число главных контуров равно числу хорд, причем сумма главных контуров и главных сечений равна числу ветвей графа. На рис. 1.8, б главные контуры обозначены цифрами 1, 2, 3. Топологические свойства графа (его структура) могут быть записаны аналитически с помощью матриц: узловой (А), контурной (В) и сечений (Q). Узловая матрица (иногда ее называют матрицей соединений) описывает соединение ветвей по отношению к узлам, контурная – по отношению к главным контурам, а сечений – по отношению к главным сечениям. Матрицы представляют собой таблицы с числом столбцов, равным числу ветвей, и числом строк, равным числу узлов без единицы, числу главных контуров и числу главных сечений соответственно для узловой, контурной и сечений. Коэффициенты матрицы равны +1, если ветвь принадлежит данному узлу, контуру или сечению, причем направление ветви совпадает с положительным направлением по отношению к узлу, контуру и сечению. В противном случае коэффициент матрицы равен –1. Если ветвь не принадлежит узлу, контуру или сечению, коэффициенты матриц – нулевые. Для графа по рис. 1.8, б узловая матрица:
Узел, для которого строка матрицы не заполняется, называют базисным. Его выбирают произвольно. В данном примере за базисный узел принят узел d. Матрицы контуров и сечений для этого же графа, имеют вид:
РЕШЕНИЕ. Обратим внимание, что ветвь 2 является общей для контуров 1 и 2; ветвь 3 – для контуров 1 и 3; ветвь 5 – для контуров 2 и 3. Изобразив эти ветви, как показано на рис. 1.9, и дополнив образованное дерево (подграф) ветвями связи согласно заданной матрице, получаем соответствующий граф.
ОБЩИЕ ВОПРОСЫ ФОРМИРОВАНИЯ УРАВНЕНИЙ
Исследование электрических цепей может преследовать различные цели. Наиболее часто требуется произвести полный расчет токов и напряжений цепи известной структуры по заданным воздействиям (источникам). В этом случае говорят о з а д а ч е а н а л и з а э л е к т р и ч е с к о й ц е п и. Анализ может быть частичным, если требуется рассчитать выходную величину – реакцию цепи на действие входного воздействия. Такую задачу называют анализом по входу и выходу. Иногда исследование цепи выполняют для определения ее параметров. Их находят по результатам измерения токов и напряжений на отдельных участках цепи. Такое исследование – задача диагностики. Если исследование имеет цель определить структуру и параметры элементов цепи, обеспечивающих необходимое преобразование входной величины, говорят о з а д а ч е с и н т е з а. Задачи синтеза – основа конструирования любого электротехнического устройства. Это наиболее сложный раздел теории электрических цепей. Ниже рассматриваются вопросы, связанные с анализом цепей. Анализ цепи, как следует из вышесказанного, заключается в отыскании токов и напряжений ветвей, число которых (n) определяет число неизвестных: n неизвестных токов и n неизвестных напряжений (2n). Первый этап анализа – составление системы независимых уравнений, позволяющих определить все неизвестные или отдельные из них согласно требованиям конкретной задачи. Система формируется из уравнений двух типов: 1) уравнений, описывающих характеристики ветвей – зависимости между напряжениями и токами; 2) уравнений, отображающих информацию о структуре (соединениях) цепи. Уравнения характеристик ветвей (как и отдельных элементов) называют к о м п о н е н т н ы м и. Компонентными уравнениями являются: закон Ома, взаимосвязи между напряжением и током индуктивного и емкостного элементов (табл. 1.1), токов и ЭДС зависимых источников с величиной управления (табл. 1.2). Компонентные уравнения ветвей, состоящих из группы элементов, например, представленных на рис. 1.6, а и 1.6, б, получают суммированием напряжений и токов отдельных элементов. Для ветвей по рис. 1.5 компонентными будут уравнения (1.5). Компонентные уравнения не связаны между собой, они относятся только к одной определенной ветви. Уравнения второго типа называют структурными уравнениями или уравнениями соединений. Они составляются по законам Кирхгофа (1.2), которые определяют равновесие токов (первый закон) и равновесие напряжений (второй закон) цепи. Первый закон применим к узлам и сечениям электрических схем. Его формулировка: для любой электрической цепи (с сосредоточенными параметрами), для любого из ее узлов (сечений) и для любого момента времени алгебраическая сумма токов всех ветвей, присоединенных к узлу (входящих в сечение), равна нулю. Второй закон применим к контурам. Он гласит: для любой цепи (с сосредоточенными параметрами), для любого из ее контуров, для любого момента времени алгебраическая сумма напряжений ветвей, образующих контур, равна нулю. Входящие в уравнения (1.2) величины суммируются алгебраически. Положительными считаются величины, совпадающие с положительными направлениями для узла, сечения или контура. Иногда второй закон Кирхгофа записывают в форме:
где напряжения источников ЭДС заменены значениями ЭДС этих источников. При такой записи со знаком ²плюс² учитываются ЭДС источников, направление действия которых совпадает с направлением обхода контура. Чтобы система структурных уравнений не была избыточной, по первому закону Кирхгофа составляются уравнения только для главных сечений или для всех узлов, кроме одного (базисного). По второму закону Кирхгофа уравнения записывают т о л ь к о для главных контуров.
ПРИМЕР 1.4. Составить систему независимых уравнений для полного анализа цепи по рис. 1.7, а.
РЕШЕНИЕ. В схеме два узла и три главных контура, поэтому по первому закону Кирхгофа нужно составить одно уравнение, а по второму – три. Для узла а имеем:
Уравнения для главных контуров (рис. 1.7, а и 1.8, а):
Выбирая в качестве независимых переменных токи ветвей, переписываем уравнения для контуров с учетом компонентных уравнений табл. 1.1:
ЗАМЕЧАНИЕ. Для схем, которые изображаются на плоскости чертежа без пересечения ветвей (их называют планарными), в качестве главных контуров проще всего выбирать элементарные ячейки, образованные ветвями. Схемы рис. 1.7 и их графы – планарные, поэтому в приведенном примере в качестве третьего главного контура можно было принять ячейку, образованную ветвями 3 и 4, уравнение которой Если ввести в рассмотрение векторы (столбцовые матрицы) для токов и напряжений ветвей
то систему независимых структурных уравнений можно записать в матричной форме: (A)(i) = 0 – первый закон Кирхгофа для узлов; (1.8) (Q)(i) = 0 – первый закон Кирхгофа для главных сечений; (1.9) (B)(u) = 0 – второй закон Кирхгофа для главных контуров. (1.10)
ОСНОВНЫЕ МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕКИХ ЦЕПЕЙ
Вынужденные составляющие в виде постоянной величины и периодической синусоидальной функции времени (частное решение дифференциального уравнения) называют установившимися составляющими, поскольку они характеризуют установившийся режим цепи после затухания свободной составляющей. Режим перехода цепи от одного установившегося состояния к другому принято называть переходным процессом или режимом. Ниже рассматриваются методы расчета цепей в установившемся режиме.
КОМПЛЕКСНЫЙ МЕТОД
Токи и напряжения, изменяющиеся во времени по синусоидальному закону, записывают:
где
Число периодов в секунду называют циклической или просто частотой
Амплитуда, частота и начальная фаза полностью характеризуют синусоидально изменяющуюся величину, однако на практике для оценки действия синусоидальных токов и напряжений вводят действующее и среднее (по модулю) значения.
Действующим или среднеквадратичным называют величину:
На действующие значения градуируются приборы, предназначенные для измерения переменных токов и напряжений. Среднее значение по модулю определяется:
На средние значения градуируются приборы, предназначенные для измерения постоянных токов и напряжений. На рис. 2.1 показаны временной график синусоидальной функции (а) и ее векторное изображение или векторная диаграмма (б).
а б Рис. 2.1 Нетрудно представить, что операции с синусоидальными токами и напряжениями, имеющими различные начальные фазы, в тригонометрической и графической формах сложны и громоздки. Поэтому широкое распространение получил комплексный (символический) метод. Суть его - в представлении синусоидальных функций одинаковой частоты функциями комплексной частоты. Для перехода от функций времени к функциям комплексной частоты используют формулу Эйлера: Если ввести в рассмотрение знак соответствия При сложении (вычитании) комплексных чисел их записывают в алгебраической форме и отдельно складывают (вычитают) их действительные и мнимые части. Например, если а то где Умножение и деление комплексных величин производят, как правило, в показательной форме:
В комплексной форме дифференцирование по времени соответствует умножению, а интегрирование - делению комплексных значений рассматриваемых функций на jw, так что:
Величины XL и XC - индуктивное и емкостное сопротивления гармоническому току; Z L и Z C – соответственно индуктивное и емкостное сопротивления в комплексной форме. Для резистивного элемента напряжение в комплексной форме определяется: uR = R × i где Z R = R - величина вещественная. Если пользоваться действующими значениями, тогда: U R = Z R × I; U L = Z L × I; U C = Z C × I. Примеры определения входных (эквивалентных) комплексных сопротивлений двухполюсников, состоящих (образованных) из R, L, C – элементов приведены в табл. 2.1. Таблица 2.1
Величину, обратную комплексному сопротивлению, называют комплексной проводимостью Выражения комплексных сопротивления Z и проводимости Y для любого двухполюсника содержат информацию как о соотношении между действующими (амплитудными) значениями тока I и напряжения U, так и фазовом сдвиге между ними:
Вещественная и мнимая части комплексного сопротивления представляют его активное R и реактивное X сопротивления:
Аналогично вещественная и мнимая части комплексной проводимости Y представляют активную G и реактивную b проводимости:
Нетрудно установить, что
Соотношения между R, X, Z, G, b, y иногда изображают графически в виде треугольников сопротивлений и проводимостей, показанных на рис. 2.2, а и б соответственно.
а б Рис. 2.2 Согласно рис. 2.2, активные и реактивные сопротивления и проводимости без фазового множителя
ПРИМЕР 2.1. Определите комплексную амплитуду тока, изменяющегося по закону i(t) = 10sin(100t + 300).
РЕШЕНИЕ. Комплексная амплитуда представляет собой функцию, модуль которой равен амплитуде заданной функции времени, а фазовый множитель еjY определяется ее начальной фазой во временной области. Таким образом, I m = 10ej30 или в алгебраической форме I m = 8,65 + j5.
ПРИМЕР 2.2. Определить входные комплексные сопротивления цепи по рис. 2.3 с элементами R = 10 Ом; L = 50 мГн; С = 1 мФ на частотах w1 = 0 и w2 = 100 рад/с.
РЕШЕНИЕ. Сопротивления элементов цепи представляем в комплексной форме: Z R = R; Z L = jwL и Z C = Рис. 2.3
Подставляя численные значения параметров элементов для частоты w1 = 0, получаем:
Для частоты w2 = 100 рад/с имеем:
ЗАМЕЧАНИЯ. 1. Сигнал с частотой w1 = 0 и периодом Т = ¥ является постоянным во времени, поэтому входное сопротивление данной цепи чисто вещественное, соответствующее сопротивлению R. 2. Отсутствие мнимой составляющей в комплексном сопротивлении Z (100) на частоте w2 = 100 рад/с объясняется взаимной компенсацией сопротивлений индуктивности и емкости. Уравнения цепи в комплексной форме записывают на основе законов Кирхгофа, как показано в табл. 2.2. Для однозначности записи уравнений цепи соблюдают следующие правила: 1. Положительные направления напряжений ветвей совпадают с произвольно выбранными положительными направлениями токов; 2. При записи первого закона Кирхгофа токи, выходящие из узла, считаются положительными, а входящие в узел - отрицательными;
Таблица 2.2
3. При записи второго закона Кирхгофа положительным считают напряжение, направление которого совпадает с направлением обхода контура; 4. Положительные направления напряжения и тока на источниках энергии - противоположны. Например, для узла, изображенного на рис. 2.4, а, следует записать: | ||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 ВВЕДЕНИЕ
ВВЕДЕНИЕ всегда положительная (W > 0).
всегда положительная (W > 0).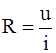 , [R] = Ом; индуктивностью
, [R] = Ом; индуктивностью  , [L] = Гн (генри); емкостью
, [L] = Гн (генри); емкостью  , [C] = Ф (фарад).
, [C] = Ф (фарад).
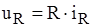








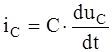

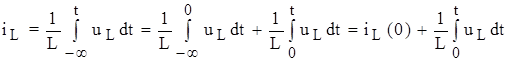 ; (1.3)
; (1.3) . (1.4)
. (1.4) РЕШЕНИЕ. Поскольку закон изменения тока известен, определяем искомые напряжения по характеристикам элементов, согласно табл. 1.1, на резистивном элементе
РЕШЕНИЕ. Поскольку закон изменения тока известен, определяем искомые напряжения по характеристикам элементов, согласно табл. 1.1, на резистивном элементе В;
В; В,
В, принято равным нулю.
принято равным нулю.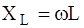 , сопротивление емкостного элемента
, сопротивление емкостного элемента 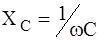 .
.
 .
.
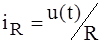 (табл. 1.1), поэтому на рис. 1.2, в показан закон изменения тока, повторяющий закон изменения входного напряжения.
(табл. 1.1), поэтому на рис. 1.2, в показан закон изменения тока, повторяющий закон изменения входного напряжения.

 .
.



 ;
;  .
.
 ;
;  .
.
 .
.

 ;
;  .
.
 ,
,  ,
, 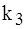 ,
,  - коэффициенты управления
- коэффициенты управления
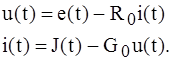 (1.5)
(1.5) - напряжение на разомкнутых зажимах источника (холостого хода),
- напряжение на разомкнутых зажимах источника (холостого хода),  - ток при коротком замыкании на его зажимах.
- ток при коротком замыкании на его зажимах.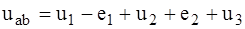 ,
, и
и  взяты с обратными знаками).
взяты с обратными знаками). . (1.6)
. (1.6) или
или  (1.7)
(1.7)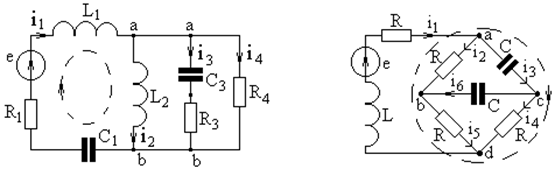
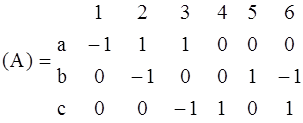
 ;
;  .
. ПРИМЕР 1.3. По заданной контурной матрице (В) нарисовать граф цепи.
ПРИМЕР 1.3. По заданной контурной матрице (В) нарисовать граф цепи.
 , (1.2, а)
, (1.2, а) .
. ;
; ;
;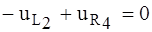 .
.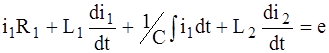 ;
; ;
; .
. . Выбор направления обхода ячеек – произвольный.
. Выбор направления обхода ячеек – произвольный. ;
;  ,
, ,
,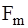 - амплитуда или максимальное значение,
- амплитуда или максимальное значение, ) – фаза, измеряемая в радианах или градусах,
) – фаза, измеряемая в радианах или градусах,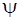 - начальная фаза, определяющая значение функции при t = 0,
- начальная фаза, определяющая значение функции при t = 0, - угловая частота (рад/с), определяющая период колебаний
- угловая частота (рад/с), определяющая период колебаний .
.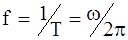 , измеряемой в герцах (Гц).
, измеряемой в герцах (Гц). .
. .
.
 , где
, где  - мнимая единица (йот). Согласно этой формуле,
- мнимая единица (йот). Согласно этой формуле,  , где
, где 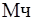 обозначает мнимую часть комплексного числа, которое, в свою очередь, можно представить
обозначает мнимую часть комплексного числа, которое, в свою очередь, можно представить  . Здесь
. Здесь  - фазовый множитель, а
- фазовый множитель, а  - временной множитель.
- временной множитель. , то для фиксированного момента времени t = 0 будем иметь: f(t)
, то для фиксированного момента времени t = 0 будем иметь: f(t) 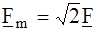 . Здесь
. Здесь  - комплексная амплитуда;
- комплексная амплитуда;  - комплексное действующее значение функции.
- комплексное действующее значение функции. ,
, ,
, ,
, ;
;  .
. ;
; .
.

 ;
;
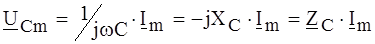 .
.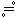 U mR = R × I m = Z R × I m ,
U mR = R × I m = Z R × I m ,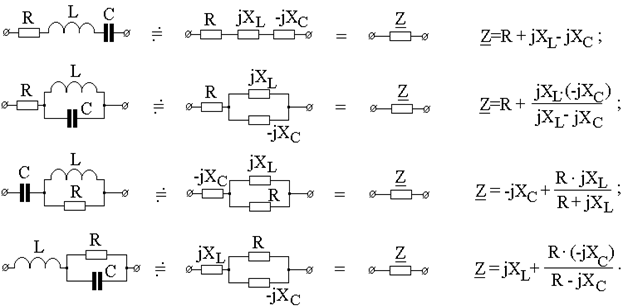

 . Как следует из приведенной табл. 2.1, при последовательном соединении пассивных элементов суммируются алгебраически их комплексные сопротивления, а при параллельном – комплексные проводимости.
. Как следует из приведенной табл. 2.1, при последовательном соединении пассивных элементов суммируются алгебраически их комплексные сопротивления, а при параллельном – комплексные проводимости.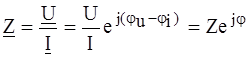 ;
;  .
. .
. .
. ;
; 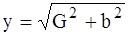 ;
;  .
.
 складывать н е л ь з я.
складывать н е л ь з я.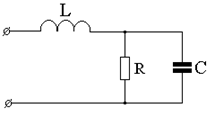
 . Эквивалентное комплексное сопротивление по отношению к входным зажимам:
. Эквивалентное комплексное сопротивление по отношению к входным зажимам: .
.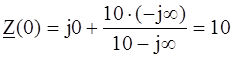 Ом.
Ом.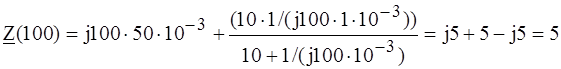 Ом.
Ом.




 или
или 
 ,
,
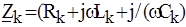 или
или




