
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее Уравнение высоты треугольника abc из точки a При (–1, 2), b(3, 1), c(5, –1) имеет видСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
x – y + 3 = 0 Общее уравнение медианы треугольника ABC из точки A при A(–1, 2), B(3, 1), C(5, –1) имеет вид 2x + 5y – 8 = 0 Общее уравнение плоскости, проходящей через точку M(1, 2, 3) и ось OY, имеет вид 3x – z = 0 Общее уравнение прямой, отсекающей на осях OX и OY отрезки длины 3 и 2 соответственно, имеет вид 2x + 3y – 6 = 0 Оператор А(x) = λx, где λ – некоторое действительное число, называется оператором _____ (слово) подобия Определитель ∆ = Определитель ∆ = Определитель ∆ = Определитель ∆ = Определитель detA = –2 Определитель Определитель диагональной матрицы равен _____ элементов главной диагонали (слово) произведению Определитель матрицы А = Определитель матрицы А = –18 Ось симметрии кривой x – y2 + 4у – 1 = 0 параллельна координатной оси _______ (слово) абсцисс Плоскости 2x – y + 2z – 6 = 0 и 7x + λy – 3λz + 10 = 0 перпендикулярны при λ, равном ___ (число) Площадь квадрата, две стороны которого расположены на прямых 3x – 4y + 3 = 0 и 3x – 4y – 2 = 0, равна ___ кв. ед. Представление вектора базису При транспортировании матрицы её определитель _____ (что делает?) не меняется Прямая Прямая –10 Пусть z = 2(cos 4(cosπ + isinπ) Равенство угловых коэффициентов двух прямых есть условие __________ этих прямых (слово) параллельности Радиус окружности x2 + y2 – 2x + 2y – 2 = 0 равен ___ (число) Радиус окружности x2 + y2 + 2x – 4y – 4 = 0 равен ___ (число) Размерность собственного подпространства Vλ симметричной матрицы равна ____ корня λ характеристического уравнения (слово) кратности Ранг квадратичной формы Q( Ранг матрицы А = Расположите векторы ( Расположите уравнения окружностей в порядке увеличения расстояния центра окружности от начала координат. Уравнения окружностей: а) x2 – 2x + y2 – 8 = 0; б) x2 + y2 – 4 = 0; в) x2 – 4x + y2 – 12 = 0 б) С(0, 0), а) С(1, 0), в) С(2, 0) Расстояние между вершинами гиперболы 25x2 – y2 + 25 = 0 равно ____ (число) Расстояние между вершинами кривой 9x2 – 4y2 = 36 равно ___ (слово) Расстояние между параллельными плоскостями 2x – 2y + z = 1 и 4x – 4y + 2z = 5 равно ___ (число) Расстояние между параллельными плоскостями x + 2y – 2z – 4 = 0 и x + 2y – 2z – 10 = 0 равно ____ (число) Расстояние между прямыми 4x – 3y + 8 = 0 и 4x – 3y – 7 = 0 равно ____ (число) Расстояние от начала координат до прямой 4x – 3y + 5 = 0 равно ____ (число) Расстояние от точки М0(3, –2, 0) до плоскости 2x + 3y + 6z – 14 = 0 равно ____ (число) Результатом выполнения действий i3 – 2i2 +i – 1 является число ____ Система n линейно независимых векторов базис Система n линейно независимых, ортогональных и единичных векторов пространства Rn образует _________ базис пространства Rn (слово) ортонормированный Система линейных однородных уравнений A совместная Система линейных уравнений равен Система уравнений имеет множество решений Скалярное произведение вектора Собственные векторы матрицы А, отвечающие различным собственным значениям, линейно _____ (каким? слово) независимы Собственные векторы симметричной матрицы А, отвечающие различным собственным значениям, взаимно ______ (как? слово) ортогональны Собственный вектор Среди векторов Среди векторов Тангенс угла наклона прямой к оси OX называется ________ прямой (фраза) угловым коэффициентом Тригонометрическая форма комплексного числа z = i имеет вид Угловой коэффициент прямой 6x + 2y – 3 = 0 равен ___ (число) –3 Угловой коэффициент прямой, параллельной оси OX, равен ____ (число) Угловой коэффициент прямой, параллельной прямой 4x + y – 5 = 0, равен _____ (число) –4 Угловой коэффициент прямой, перпендикулярной данной прямой x + 3у – 2 = 0, равен ___ (число) Укажите верные соответствия между алгебраической и тригонометрической формами комплексного числа z = 1 – i == z = Укажите верные соответствия между алгебраической и тригонометрической формой комплексного числа z = –1 + i == z =
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 880; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.56 (0.007 с.) |

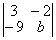 равен нулю при b, равном ___ (число)
равен нулю при b, равном ___ (число) равен нулю при λ, равном ___ (число)
равен нулю при λ, равном ___ (число)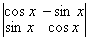 при любых x равен ___ (число)
при любых x равен ___ (число)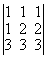 равен ___ (число)
равен ___ (число)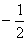 , тогда определитель det(A–1) равен ____ (число)
, тогда определитель det(A–1) равен ____ (число) равен
равен равен ____ (число)
равен ____ (число) равен ____ (число)
равен ____ (число) в виде суммы
в виде суммы  называется разложением вектора
называется разложением вектора  (наберите слово)
(наберите слово) параллельна плоскости 7x + λy – 3z + 10 = 0 при λ, равном ___ (число)
параллельна плоскости 7x + λy – 3z + 10 = 0 при λ, равном ___ (число) параллельна плоскости x – 2y – 3z + 9 = 0 при λ, равном ____ (число)
параллельна плоскости x – 2y – 3z + 9 = 0 при λ, равном ____ (число) + isin
+ isin  ) = 3x2 + 10xy + 3y2 равен ____ (число)
) = 3x2 + 10xy + 3y2 равен ____ (число)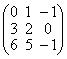 равен ____ (число)
равен ____ (число) = {0, 1, –1},
= {0, 1, –1},  = {2, 1, 1},
= {2, 1, 1}, 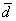 = {0, 0, –1} в порядке убывания их скалярного произведения с вектором
= {0, 0, –1} в порядке убывания их скалярного произведения с вектором  = {1, 1, 1}
= {1, 1, 1}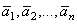 пространства Rn образует ______ этого пространства (слово)
пространства Rn образует ______ этого пространства (слово) ________ (какая? слово)
________ (какая? слово) совместна тогда и только тогда, когда ранг матрицы А ______ рангу расширенной матрицы
совместна тогда и только тогда, когда ранг матрицы А ______ рангу расширенной матрицы 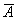 (вставить слово)
(вставить слово)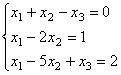
 равно ____ (число)
равно ____ (число) отвечает собственному значению λ, равному ___ (число)
отвечает собственному значению λ, равному ___ (число) ,
, 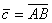 и
и  , где A(1, –1,2), B(2, –1, 0), D(1, 1, –2), равными являются
, где A(1, –1,2), B(2, –1, 0), D(1, 1, –2), равными являются
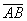 , где A(1, 3, 10), B(1, 7, –6),
, где A(1, 3, 10), B(1, 7, –6),  ,
, 
 , z = 1 +i == z =
, z = 1 +i == z = 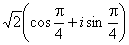 , z = i == z =
, z = i == z =  , z = 1 == z = cos00 + isin00, z = –i == z =
, z = 1 == z = cos00 + isin00, z = –i == z = 



