
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Укажите верные соответствия между системами векторов и их характеристикамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Укажите верные соответствия между системами векторов и рангом системы векторов a1 = (1, –1, 1, –1), a2 = (1, –2, 0, –3), a3 = (1, 1, –2, 3), a4 = (2, 2, –4, 6) == r = 3, a1 = (1, 2, 2), a2 = (1, 2, 3), a3 = (1, 2, –2) == r = 2, a1 = (2, 0, 1, 0), a2 = (4, 0, 2, 0), a3 = (–2, 0, –1, 0) == r = 1 Укажите верные соответствия между системами уравнений и их решениями x2 = 1, x2 = –1, Укажите верные соответствия между системой уравнений и решением этой системы Укажите верные соответствия между собственными векторами матрицы А = Укажите верные соответствия между собственными векторами матрицы А = Укажите верные соответствия между сторонами треугольника ABC и их длинами, если A(3, 0, 2), B(4, 2, 0), C(0, 4, 2) Укажите верные соответствия между уравнением и типом кривой 16x2 – 9y2 – 64x – 54y – 161 = 0 == гипербола, 5x2 + 9y2 – 30x + 18y – 9 = 0 == эллипс, y2 – 4x – 2y – 3 = 0 == парабола Укажите верные соответствия между уравнением кривой и её типом 16x2 – 9y2 – 64x – 54y – 161 = 0 == гипербола, 5x2 + 9y2 – 30x + 18y+ 9 = 0 == эллипс, x2 + y2 – 4x + 2y + 1 = 0 == окружность Укажите верные соответствия между уравнением окружности и координатами центра x2 + y2 – 2x – 6y – 6 = 0 == О(1, 3), x2 + y2 – 4x + 2y + 1 = 0 == О(2, –1), x2 + y2 + 2x – 2y – 23 = 0 == О(–1,1) Укажите верные соответствия между уравнением окружности и радиусом R этой окружности x2 + y2 – 2x – 6y – 6 = 0 == R = 4, x2 + y2 – 4x + 2y + 1 = 0 == R = 2, x2 + y2 + 2x – 2y – 23 = 0 == R = 5 Укажите верные соответствия между уравнением прямой и расстоянием от начала координат до этой прямой 3x – 4y + 5 = 0 == d = 1, 4x + 3y – 25 = 0 == d = 5, x + 3y – 10 = 0 == d = Укажите верные соответствия между уравнениями пары прямых и их взаимным расположением 2x – 3y + 1 = 0 6y – 4х = –2 == прямые параллельны, 3x – 3y + 5 = 0 x – 2y – 2 = 0 == прямые пересекаются, y + x = 2 3y = 5 + 3x == прямые перпендикулярны Укажите верные соответствия между уравнениями прямой и плоскости и их взаимным расположением 3x – 3y + 2z = 1 == прямая перпендикулярна плоскости, 3x – y – 2z – 2 = 0 == прямая лежит на плоскости, 3x – y – 2z + 4 = 0 == прямая параллельна плоскости Укажите верные соответствия между уравнениями прямых и величиной отрезка b, отсекаемого прямой на оси OY Укажите верные соответствия между уравнениями прямых и их расположением по отношению к прямой 3x – 2y + 7 = 0 2x + 3y + 6 = 0 == прямые перпендикулярные, 6x – 4y – 9 = 0 == прямые параллельные, x + y – 1 = 0 == прямые пересекаются в точке М(–1, 2) Укажите верные соответствия между уравнениями прямых и их угловыми коэффициентами Укажите верные соответствия между уравнениями прямых и точками пересечения этих прямых с осями координат 2x + 5y = 10 == A(5, 0), B(0, 2), 3x – 2y – 6 = 0 == A(2, 0), B(0, –3), 3x + 4y – 12 = 0 == A(4, 0), B(0, 3) Укажите верные соответствия между уравнениями прямых и углом, образуемым этими прямыми с прямой 5x – y + 7 = 0 10x – 2y = –14 == ϕ = 0, 2x – 3y + 1 = 0 == ϕ = Указать верные соответствия между системой векторов и типом базиса в R3, который они образуют f1 = (0, 0, 1), f2 = (0, 1, 0), f3 = (1, 0, 0) == ортонормированный базис R3, f1 = (1, 1, 1), f = (–1, 0, 1), f3 = (2, 0, –2) == система не образует базиса в R3, f1 = (1, 1, 1), f2 = (0, 1, 1), f3 = (0, 0, 1) == базис в R3 Уравнение λ2 – 2λ – 3 = 0 является ______ уравнением квадратичной формы x2 + 4xy + y2 (каким? слово) характеристическим Уравнение абсцисс Уравнение 25x2 – y2 + 25 = 0 определяет ____ (слово, название кривой) гиперболу Уравнение 4x2 + y2 – 2y – 15 = 0 определяет кривую, называемую _____ (слово) эллипсом Уравнение x – y2 + 4y – 1 = 0 определяет кривую, называемую ____ (слово) параболой Уравнение x = 0 является уравнением оси ______ (слово) ординат Уравнение x2 + y2 – 2x + 2y – 2 = 0 определяет _______ (слово, название кривой) окружность Уравнение y = 0 является уравнением оси ______ (слово) абсцисс Уравнение параболы с вершиной в начале координат, проходящей через точку (1, 2) и имеющей вертикальную директрису, имеет вид y2 = 4x Уравнение параболы с вершиной в начале координат, проходящей через точку (2, 2) и имеющей горизонтальную директрису, имеет вид x2 = 2y Уравнение с угловым коэффициентом прямой, пересекающей оси OX и OY в точках M(3, 0) и N(0, 2) имеет вид Уравнение с угловым коэффициентом прямой, проходящей через точку A(1, –1) перпендикулярно прямой 3x + 2y – 2 = 0, имеет вид Уравнение с угловым коэффициентом прямой, проходящей через точку A(1,–1) параллельно прямой 3x + 2y – 2 = 0, имеет вид Уравнения каноническими Уравнения параметрическими Установите верные соответствия между матрицами и их характеристическими многочленами А =
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 970; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.159.223 (0.006 с.) |

 = (1, 2, 3),
= (1, 2, 3),  = (0, 1, 2),
= (0, 1, 2),  = (0, 0, 1) == векторы линейно независимые, могут образовать базис R3, f1 = (1, 2, 3),
= (0, 0, 1) == векторы линейно независимые, могут образовать базис R3, f1 = (1, 2, 3), 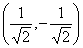 , g2 =
, g2 =  == образуют ортонормированный базис R3
== образуют ортонормированный базис R3 == x1 = –1
== x1 = –1 == x1 = 2
== x1 = 2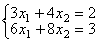 == система несовместна
== система несовместна == система имеет единственное решение
== система имеет единственное решение  ,
,  == система имеет множество решений,
== система имеет множество решений,  == система не имеет решений (несовместна)
== система не имеет решений (несовместна) и отвечающими им собственными числами
и отвечающими им собственными числами = (1, 1) == не является собственным вектором матрицы А,
= (1, 1) == не является собственным вектором матрицы А,  и отвечающими им собственными числами
и отвечающими им собственными числами = == 2
= == 2  ,
, 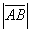 = == 3,
= == 3,  = == 5
= == 5

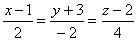
 == b = 6, 2x – 3y = 6 == b = –2, y = –3 == b = –3
== b = 6, 2x – 3y = 6 == b = –2, y = –3 == b = –3 == k = –
== k = –  , 2x – 3y = 6 == k =
, 2x – 3y = 6 == k =  , y = –3 == k = 0
, y = –3 == k = 0 , x + 5y – 10 = 0 == ϕ =
, x + 5y – 10 = 0 == ϕ = 
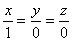 является каноническим уравнением координатной оси _____ (слово)
является каноническим уравнением координатной оси _____ (слово)

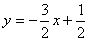
 являются _______ уравнениями прямой (слово)
являются _______ уравнениями прямой (слово) называются ________ уравнениями прямой (слово)
называются ________ уравнениями прямой (слово) == λ2 – 2λ, А =
== λ2 – 2λ, А =  == λ2 – λ – 10, А =
== λ2 – λ – 10, А =  == λ2 + 2
== λ2 + 2


