Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Все комплексные числа z, расположенные на окружностиСодержание книги Поиск на нашем сайте
Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) В пространстве многочленов степени n ≤ 2 система векторов f1 = 1, f2 = x + 1, f3 = 2x образует базис В) В пространстве многочленов степени n ≤ 2 система векторов f1 = 1, f2 = x, f3 = x2 образует стандартный базис Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Вектор В) Если вектор нормали Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Вектор В) Собственный вектор Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Векторы В) Векторы Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Выражение a + bi называется алгебраической формой записи комплексного числа В) Модуль комплекстного числа z = 1 – i равен |z| = 0 Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Гипербола – это геометрическое место точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная В) Гипербола – это геометрическое место точек плоскости, модуль разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Две плоскости перпендикулярны, если скалярное произведение их нормальных векторов равно нулю В) Две плоскости параллельны, если их нормальные векторы коллинеарны Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Для параллельности двух прямых необходимо и достаточно, чтобы их угловые коэффициенты были равны В) Для перпендикулярности двух прямых необходимо и достаточно, чтобы их угловые коэффициенты были равны по величине и обратны по знаку Подберите правильный ответ
А – да, В – нет Верны ли утверждения? А) Если определитель системы равен нулю, то система имеет единственное решение В) Если система имеет единственное решение, то её определитель отличен от нуля Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Если определитель системы равен нулю, то система имеет единственное решение В) Если система имеет единственное решение, то её определитель отличен от нуля Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Если переставить местами две строки, то определитель изменит знак В) При транспонировании определитель не меняется Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Если переставить местами две строки, то определитель не изменится В) Если переставить местами две строки матрицы, то её ранг не изменится Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Квадратичная форма x2 – 4xy + 5y2 отрицательно определена В) Квадратичная форма отрицательно определена, если все угловые миноры её матрицы отрицательны Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Квадратичная форма –x2 + 2xy – 2y2 отрицательно определена В) Матрица А = Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Квадратичная форма положительно определенная, если все её собственные числа положительны В) Квадратичная форма отрицательно определенная, если все её собственные чилса отрицательны Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Корень В) Корень Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Корень В) Корень Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Кривая x2 – xy + 5y2 – 7 = 0 эллиптического типа В) Кривая x2 + 4xy + y2 + 10 = 0 эллиптического типа Подберите правильный ответ А – да, В – нет Верны ли утверждения?
А) Любая зависимая система векторов в Rn образует базис, если всякий вектор в Rn является линейной комбинацией векторов этой системы В) Ортогональная система векторов линейно независима Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Любой вектор В) Действительное число λ есть собственное число матрицы А, если λ является корнем уравнения det(A – λE) = 0 Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Матрица А = В) Квадратичная форма 4x2 – 2xy + y2 является положительно определенной Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Матрица А имеет обратную тогда и только тогда, когда её определитель не равен нулю В) Матрица А называется невырожденной, если её определитель равен нулю Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Матрица В назывется обратной к матрице А, если АВ = ВА = Е В) Если верно равенство А =АТ, то матрица А – симметричная Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Матрица квадратичной формы, записанной в каноническом виде, является диагональной В) Симметричная матрица имеет собственный ортонормированный базис Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Матрицей квадратичной формы Q( В) Матрица А = Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Ненулевой вектор В) Две плоскости параллельны, если их нормальные векторы ортогональные Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Окружность – геометрическое место точек, равноудаленных от точки C(a, b), называемой центром окружности В) Окружность – это геометрическое место точек, сумма расстояний которых до двух данных точек есть величина постоянная Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Орты В) Представление вектор Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Парабола – центральная кривая второго порядка В) Парабола имеет две оси симметрии Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) При транспонировании матрицы её определитель меняется В) Определитель равен нулю, если элементы двух строк или столбцов равны или прапорциональны Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) При транспонировании матрицы её ранг изменяется В) Операция перемножения матриц перестановочна Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Размерностью подпространства называется число векторов в базисе этого подпространства В) Система любых векторов Подберите правильный ответ
А – да, В – нет Верны ли утверждения? А) Ранг квадратичной формы равен числу отличных от нуля коэффициентов в любом её каноническом виде В) Квадратичная форма называется отрицательно определенной, если Q( Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Ранг ступенчатой матрицы равен числу её угловых элементов В) При перестановке двух строк матрицы её ранг увеличивается Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Система уравнений В) Система уравнений Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Систему В) Если ранг матрицы системы меньше ранга расширенной матрицы системы r(A) <> Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Скалярные квадраты ортов В) Длина вектора Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Собственному числу λ отвечает единственный собственный вектор В) Многочлен λ2 – 1 является характеристическим многочленом матрицы Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Угловым коэффициентом прямой называется тангенс угла наклона прямой к оси OY В) Угловой коэффициент прямой, параллельной оси OY, равен нулю Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Уравнение det(A – λE) = 0 называется характеристическим многочленом матрицы А В) Уравнение λ2 – 1 = 0 является характеристическим для матрицы Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Уравнение оси OX имеет вид: y = 0 В) Уравнение оси OY на плоскости имеет вид: x = 0 Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Число λ = 1 является собственным числом матрицы В) Число λ = 2 является собственным числом матрицы Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Эксцентрасистет эллипса меньше единицы В) Эксцентриситет гиперболы больше единицы Подберите правильный ответ А – да, В – да Подберите правильный ответ А – да, В – нет
Верны ли утверждения? А) В пространстве многочленов степени n ≤ 2 система векторов f1 = 1, f2 = x + 1, f3 = 2x образует базис В) В пространстве многочленов степени n ≤ 2 система векторов f1 = 1, f2 = x, f3 = x2 образует стандартный базис Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Вектор В) Если вектор нормали Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Вектор В) Собственный вектор Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Векторы В) Векторы Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Выражение a + bi называется алгебраической формой записи комплексного числа В) Модуль комплекстного числа z = 1 – i равен |z| = 0 Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Гипербола – это геометрическое место точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная В) Гипербола – это геометрическое место точек плоскости, модуль разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Две плоскости перпендикулярны, если скалярное произведение их нормальных векторов равно нулю В) Две плоскости параллельны, если их нормальные векторы коллинеарны Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Для параллельности двух прямых необходимо и достаточно, чтобы их угловые коэффициенты были равны В) Для перпендикулярности двух прямых необходимо и достаточно, чтобы их угловые коэффициенты были равны по величине и обратны по знаку Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Если определитель системы равен нулю, то система имеет единственное решение В) Если система имеет единственное решение, то её определитель отличен от нуля Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Если определитель системы равен нулю, то система имеет единственное решение В) Если система имеет единственное решение, то её определитель отличен от нуля Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Если переставить местами две строки, то определитель изменит знак В) При транспонировании определитель не меняется Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Если переставить местами две строки, то определитель не изменится
В) Если переставить местами две строки матрицы, то её ранг не изменится Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Квадратичная форма x2 – 4xy + 5y2 отрицательно определена В) Квадратичная форма отрицательно определена, если все угловые миноры её матрицы отрицательны Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Квадратичная форма –x2 + 2xy – 2y2 отрицательно определена В) Матрица А = Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Квадратичная форма положительно определенная, если все её собственные числа положительны В) Квадратичная форма отрицательно определенная, если все её собственные чилса отрицательны Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Корень В) Корень Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Корень В) Корень Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Кривая x2 – xy + 5y2 – 7 = 0 эллиптического типа В) Кривая x2 + 4xy + y2 + 10 = 0 эллиптического типа Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Любая зависимая система векторов в Rn образует базис, если всякий вектор в Rn является линейной комбинацией векторов этой системы В) Ортогональная система векторов линейно независима Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Любой вектор В) Действительное число λ есть собственное число матрицы А, если λ является корнем уравнения det(A – λE) = 0 Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Матрица А = В) Квадратичная форма 4x2 – 2xy + y2 является положительно определенной Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Матрица А имеет обратную тогда и только тогда, когда её определитель не равен нулю В) Матрица А называется невырожденной, если её определитель равен нулю Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Матрица В назывется обратной к матрице А, если АВ = ВА = Е В) Если верно равенство А =АТ, то матрица А – симметричная Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Матрица квадратичной формы, записанной в каноническом виде, является диагональной В) Симметричная матрица имеет собственный ортонормированный базис Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Матрицей квадратичной формы Q( В) Матрица А = Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) Ненулевой вектор В) Две плоскости параллельны, если их нормальные векторы ортогональные Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Окружность – геометрическое место точек, равноудаленных от точки C(a, b), называемой центром окружности В) Окружность – это геометрическое место точек, сумма расстояний которых до двух данных точек есть величина постоянная Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Орты В) Представление вектор Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Парабола – центральная кривая второго порядка В) Парабола имеет две оси симметрии Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) При транспонировании матрицы её определитель меняется В) Определитель равен нулю, если элементы двух строк или столбцов равны или прапорциональны Подберите правильный ответ А – нет, В – да Верны ли утверждения? А) При транспонировании матрицы её ранг изменяется В) Операция перемножения матриц перестановочна Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Размерностью подпространства называется число векторов в базисе этого подпространства В) Система любых векторов Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Ранг квадратичной формы равен числу отличных от нуля коэффициентов в любом её каноническом виде В) Квадратичная форма называется отрицательно определенной, если Q( Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Ранг ступенчатой матрицы равен числу её угловых элементов В) При перестановке двух строк матрицы её ранг увеличивается Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Система уравнений В) Система уравнений Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Систему В) Если ранг матрицы системы меньше ранга расширенной матрицы системы r(A) <> Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Скалярные квадраты ортов В) Длина вектора Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Собственному числу λ отвечает единственный собственный вектор В) Многочлен λ2 – 1 является характеристическим многочленом матрицы Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Угловым коэффициентом прямой называется тангенс угла наклона прямой к оси OY В) Угловой коэффициент прямой, параллельной оси OY, равен нулю Подберите правильный ответ А – нет, В – нет Верны ли утверждения? А) Уравнение det(A – λE) = 0 называется характеристическим многочленом матрицы А В) Уравнение λ2 – 1 = 0 является характеристическим для матрицы Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Уравнение оси OX имеет вид: y = 0 В) Уравнение оси OY на плоскости имеет вид: x = 0 Подберите правильный ответ А – да, В – да Верны ли утверждения? А) Число λ = 1 является собственным числом матрицы В) Число λ = 2 является собственным числом матрицы Подберите правильный ответ А – да, В – нет Верны ли утверждения? А) Эксцентрасистет эллипса меньше единицы В) Эксцентриситет гиперболы больше единицы Подберите правильный ответ А – да, В – да Все комплексные числа z, расположенные на окружности
|z| = 1 А – квадратная матрица третьего порядка и ее определитель detA = –1, тогда det(3A) равен –27 Алгебраическая форма комплексного числа 0 + i В линейном n-мерном пространстве V квадратная матрица C порядка n, столбцами которой являются координаты базиса { перехода В линейном пространстве V вектор x называется ______ вектора y = A(x) (слово) прообразом В линейном пространстве V вектор y = A(x) называется _____ вектора x (слово) образом В некотором базисе задана матрица линейного преобразования: А = если x = (0, 1), то координаты образа А(x) равны (2, 1), если x = (1, 1), то координаты образа А(x) равны (3, 1) В некотором базисе задана матрица линейного преобразования: А = если x = (–1, 2), то координаты образа А(x) равны (3, 1), если x = (2, –1), то координаты образа А(x) равны (0, –2) В пространстве C(a, b) две функции x(t) и y(t) считаются _______, если ортогональными В пространстве C(–π, π) функции sin t, cos t являются _______ (какими? слово) ортогональными В пространстве R3 базис {f} выражен через базис {g}: В пространстве R3 базис {g} выражен через базис {f}: В пространстве многочленов степени n ≤ 2 даны многочлены: P1(x) = (x + 1)2; P2(x) = (1 – x)2; P3(x) = 3x2 + x. Расположите многочлены в порядке возрастания их максимальной координаты в базисе l1 = 1, l2 = x, l3 = x2 P2(x), P1(x), P3(x) В пространстве многочленов степени n ≤ 2 даны многочлены: P1(x) = (x + 1)2; P2(x) = (x – 1)2; P3(x) = 3x2 + 5x – 1. Расположите многочлены в порядке возрастания максимальных координат их в базисе l1 = x2, l2 = x, l3 = 1 P2(x), P1(x), P3(x) В пространстве многочленов степени n ≤ 2 даны многочлены: P1(x) = (x + 1)2; P2(x) = (x – 1)2; P3(x) = 3x2 + 5x – 1. Расположите многочлены в порядке возрастания минимальных координат их в базисе l1 = x2, l2 = x, l3 = 1 P2(x), P3(x), P1(x) В пространстве многочленов степени n ≤ 2 даны многочлены: P1(x) = (x + 1)2; P2(x) = (x – 1)2; P3(x) = 3x2 + 5x – 1. Расположите многочлены в порядке убывания максимальных координат в базисе l1 = x2, l2 = x, l3 = 1 P5(x), P1(x), P2(x) В пространстве многочленов степени n ≤ 2 даны три многочлена: P1(x) = 2(x + 1)2 – 2; P2(x) = (x + 1)2 + 3x + 4; P3(x) = (x + 1)2 – 3x + 1. Расположите многочлены в по-рядке возрастания максимальной координаты их в базисе l1 = (x + 1)2, l2 = x, l3 = 1 P3(x), P1(x), P2(x) В пространстве многочленов степени n ≤ 2 задана функция f(x) = x2 – 2x + 1 координаты f(x) в базисе {x2, 2x, 1} равны (1, –1, 1), координаты f(x) в базисе {x2, x, 1} равны (1, –2, 1) В пространстве многочленов степени n ≤ 2 задана функция f(x) = x2 + 2x + 3 координаты f(x) в базисе {1, x, x2} равны (3, 2, 1), координаты f(x) в базисе {x2, x + 1, 1} равны (1, 2, 1) В пространстве многочленов степени n ≤ 2 с базисом {1, x2, x} координаты (2, 1, 3) определяют многочлен f(x) = x2 + 3x + 2, координаты (–3, 0, 2) определяют многочлен f(x) = 2x – 3 В пространстве многочленов степени n ≤ 2 с базисом {x, x2, 2} координаты (1, 1, –1) определяют многочлен f(x) = x2 + x – 2, координаты (2, 2, 2) определяют многочлен f(x) = 2x2 + 2x + 4 В пространстве многочленов степени n ≤ 2 с базисом {x2, 2x, 1} координаты (1, –1, 4) определяют многочлен f(x) = x2 – 2x + 4, координаты (2, 0, 5) опре
|
|||||||||
|
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 771; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.208.191 (0.011 с.) |
, перпендикулярный данной прямой, называется направляющим вектором прямой в пространстве
к плоскости коллинеарен направляющему вектору 
= (1, 2) является свобственным вектором матрицы А = 
= (1, 1, 1), 
= (1, 1, 0), 
= (2, 2, 1) образуют базис в R3
является матрицей квадратичной формы x2 + 2xy – 2y2
имеет одно значение, равное 1
не существует
, называется собственным вектором матрицы А
является матрицей квадратичной формы x2 + 4xy – y2
является матрицей квадратичной формы x2 + 2xy + y2
, 
, 
образуют базис трехмерного векторного пространства R3
в виде суммы компонент называется разложением вектора 
по базису 
, 
,…, 
из Rm образует базис пространства Rm
совместна тогда и только тогда, когда ранги матриц системы и расширенной матрицы системы совпадают
нельзя решить методом Крамера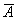
), то система имеет единственное решение
, удовлетворяют условию
имеет вид
} по базису { 
}, называется матрицей ______ от базиса {f} к базису {g} (слово)
(t) ⋅ y(t)dt = 0 (какими? слово)
. Матрица перехода от базиcа {g} к базису {f} равна
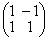
. Матрица перехода от базиcа {f} к базису {g} равна
