
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диф уравнение с разделяющимися переменными. Однородные диф уравненияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Уравнения с разделяющимися переменными. называется дифференциальное уравнение вида f(x)dx + g(y)dy = 0 с непрерывными функциями f(х) и g(y). Равенство Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x0) = y0 или в виде x(y0) = x0. Уравнением с разделяющимися переменными называется дифференциальное уравнение вида f1(x)g1 (y)dx + f2(x) g2(y)dy =0. Функции f1(x), g1(y), f2(x), g2(y) непрерывны в cвоих областях определения и g1(y)f2(x) ≠ 0. Разделив обе части уравнения на отличное от нуля произведение g1(y)f2(x), получим уравнение с разделенными переменными Общий интеграл этого уравнения имеет вид
27. ЛДУ 1-го порядка (вывод формулы общего решения) ДУ вида A(x)y’+B(X)y+C=0, где A(x)≠0, или после деления на A(x), приведённое к виду y’+p(x)y=q(x), называется линейным ДУ первого порядка. Если q(x) Линейное однородное уравнение – это уравнение с разделяющимися переменными, его общее решение выражается формулой Для решения линейного неоднородного уравнения можно применять метод вариации произвольной постоянной, тогда общее решение неоднородного уравнения получается в виде y(x) = u(x) v(x): из этого выражения находим u(x), и y(x) = u(x) v(x). Линейное неоднородное уравнение может быть сведено к решению двух уравнений с разделяющимися переменными при помощи подстановки(метод Бернулли)y(x) = u(x) v(x) двух неизвестных дифференцируемых ф-и й u(x) и v(x).Тогда Найдем функцию v(x) как некоторое ненулевое частное реш-е однородного ур-я
28,29. Линейные диф ур-я второго порядка с пост коэффициентами. имеет вид Линейным однородным уравнением второго порядка называется уравнение Общее реш-е линейного однородного диф.ур-я имеет вид: y=C1y1(x)+C2y2(x) Для неоднородного линейного ур-я общее реш-е имеет вид:y= C1y1(x)+C2y2(x)+µ(x) Еслиp(x)≡p, q(x)≡q – постоянные, то линейное ур-е Возможны 3 вар-та: D>0 корни ур-яλ1, λ2различные. Общее реш-е однородногоур-я y=C1eλ1x+C2eλ2x D=0 корниλ1=λ2=λодинаковые. тогдереш-е y=eλx(C1+C2x) D<0 корни ур-я λ1,2=α+/-iβ(i=корень из -1). реш-е y=
30. Лин неоднор ДУ 2-го порядка с пост коэфф-ми. Рассмотрим уравнение y´´+py´+qy=r(x) /где p,q? R, r(x)-функция. которое имеет вид y=yO+yЧ, где yO-общее решение уравнения y´´+py´+qy =0 yЧ-частное решение уравнения y´´+py´+qy=r(x), которое зависит от вида правой части,т.е r(x) Рассмотрим некоторые частные случаи: 1) r(x)=Pn(x),где Pn(x) – многочлен степени «n» В этом случае решение yЧ ищут из уравнения к²+pк+q=0 в виде: • yЧ=Qn(x) при q≠0 • yЧ=x Qn(x) q=0, p≠0 • yЧ=x² Qn(x) q=p=0 2) r(x)=а Вид частного решения следущее: • yЧ=А (корни некратные,некомплексные) • yЧ=Аx •yЧ=Аx² 3) r(x)=acosmx+bsinmx где a,b,m=const • yЧ= Acosmx+Bsinmx при условии что p²+(q-m²)≠0 • yЧ= x(Acosmx+Bsinmx) если p²+(q-m²)=0, p=0,q= m²
31. Определение ряда и его сходимость Определение 1. Пусть задана бесконечная числовая последовательность u1, u2,…,un,…. Выражение Члены ряда опред след суммы: S1=a1, S2=a1+a2,Sn=a1+a2+…+an; Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда: Определение 3. Если существует конечный предел Теорема. Для того, чтобы ряд сходился необходимо и достаточно, чтобы
32. Необходимый признак сходимости ряда (док-во). Теорема. Если ряд сходится, то Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел Следствие. Если Рассмотренный признак является только необходимым, но не достаточным, то есть из того, что Чтобы числовой ряд сходился необходимо и достаточно, чтобы
33. Основные свойства сходящихся и несходящихся рядов Сходящихся: 1. Отбрасывание конечного числа членов ряда (или добавление к ряду конечного числа членов) не влияет на сходимость или расходимость этого ряда. 2. Сумма сход числ ряда умнож на const равно его сумме умнож на ту же const. 3. Если числ ряды Сходимость ряда, составленного из членов геометрической прогрессии. Ряд, составленный из членов геометрической прогрессии со знаменателем q и с первым членом a1, a1≠0, вида a1+a1q+a1q2+…+a1qn-1+…= Частичная сумма ряда Рассмотрим 4 случая 1. При и ряд будет сходящимся.
Сумма Sn первых его n членов, равная na, при
4. Если | q |>1, тогда Гармонический ряд Ряд вида Обобщенный гармонический ряд, или ряд Дирихле – это ряд вида
Ряд
34. Достаточные признаки сходимости знакоположительных числовых рядов Числовой ряд называется знакоположительным, если un >0 при всех n =1,2,3…. Для таких рядов частичные суммы S1, S2, …, Sn,… образуют возрастающую числовую последовательность S1 < S2 <…< Sn <…. Признак сравнения числовых рядов Пусть даны два знакоположительных числовых ряда причём 0<a n≤bn при любых n =1,2,…. Тогда: 1. Если ряд 2. Если ряд В качестве эталонного числ ряда использ ряд вида Предельный признак сравнения Пусть даны два знакоположительных числовых ряда 35. Признак Даламбера Пусть дан знакоположительный числовой ряд и пусть существует предел Признак Коши Пусть дан знакоположительный числовой ряд При l <1 ряд сходится, при l >1 ряд расходится. При l =1 критерий Коши не позволяет определить сходимость/расходимость Интегральный признак (признак Маклорена-Коши) Пусть задан ряд, непрер ф-я y=f(x) на [1;∞) такая что f(n)=an. Тогда интеграл
35. Знакопеременные ряды Числ ряд наз знакомеременным, если его члены либо положит либо отрицат Признак Коши сходимости знакоперем рядов Числ ряд Если числ ряд Теорема. Из абсолютной сходимоти числ ряда след сходимость исходного ряда, т.е. если Числовой ряд вида u1-u2+u3-u4+…+ … +(- 1 )n- 1. un+ …, где un – модуль члена ряда, называется знакочередующимся числовым рядом, т.е. ряд в к-м члены попеременно меняют знак. Признак Лейбница Если для знакочередующегося числового ряда Выполняются два условия: 1. Члены ряда убывают по модулю u1 > u2 >…> un >…, 2. то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда. Следствие. Остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине, т.е.
36. Знакопеременные ряды. Абсолютная и условная сходимость. Числовой овой ряд Если ряд, сост из абсол значений величин Теорема: Если ряд явл абсол сх-ся, то исх ряд сх-ся. Док-во:восп-ся 1 признаком сравнения Рассм-м ряд
О. Если ряд, образ из абсол значений его величин расх-ся, а исх ряд сх-ся, то он наз условно сх-ся. Признак Лейбница Если для знакочередующегося числового ряда Выполняются два условия: 1. Члены ряда убывают по модулю u1 > u2 >…> un >…, 2. то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда. Следствие. Остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине, т.е. Если в знакочередующемся ряде члены ряда монотонно убывают по абсолютным значениям и imUn=0 (nà∞), то ряд сходится. Дано: U1>U2>U3>...; imUn=0 (nà∞); U1-U2+U3-U4+..., Ui>0 Доказательство: S2n ¾ чётная частичная сумма: S2n=+U1-U2+U3-U4+...-U2n; S2n=(U1-U2)+(U3-U4)+...+(U2n-1-U2n); S2n>0 ¾ возрастает. S2n=U1-(U2-U3)-(U4-U5)-...-U2n; S2n<U1, U1>0; imS2n=S {nà∞} imS2n+1 {nà∞} = im(S2n+U2n+1)=S; Чётные и нечётные суммы с одним пределом => ряд сходится. 1) Заметим, что S>0, т.е. знак суммы совпадает со знаком первого члена. 2) S<U1
38. Абсол и условная сходимость. О. Ряд вида наз знакочеред-ся. Признак Лейбница (сх-ть знакочер ряда). Для того, чтобы ряд (1) сх-ся достаточно, чтобы абсол значения убывали и →0 при возрастании n, т.е. О. Если ряд, сост из абсол значений величин Теорема: Если ряд явл абсол сх-ся, то исх ряд сх-ся. Док-во:восп-ся 1 признаком сравнения Рассм-м ряд Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно. О. Если ряд, образ из абсол значений его величин расх-ся, а исх ряд сх-ся, то он наз условно сх-ся.
39. Понятие степенного ряда. Область сходимости степенного ряда. Теорема Абеля. Ряд вида
40. Радиус сходимости и область сходимости степенных рядов. Дифференцирование и интегрирование степенных рядов Свойства степенных рядов 1. Сумма степенного ряда f(x) непрерывна внутри его интервала сходимости 2. Степенной ряд можно почленно интегрировать на любом отрезке целиком принадлежащем интервалу сходимости. Степенной ряд можно почленно дифференцировать в интервале сходимости любое число раз. Ряды полученные почленным интегрированием и почленным дифференцированием степенного ряда имеют тот же радиус сходимости что и исходный ряд. 3. Пусть задан СР 4. Для любого интеграла (α,β)
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.
где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.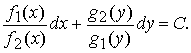

 0, то уравнение называется линейным однородным, иначе – линейным неоднородным.
0, то уравнение называется линейным однородным, иначе – линейным неоднородным. .
. .
. , и уравнение приводится к виду
, и уравнение приводится к виду 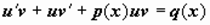 , или
, или  .
. . затем находим u(x) из уравнения
. затем находим u(x) из уравнения 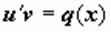 . после нахождения v(x) определяем u(x) как реш-е ур-я
. после нахождения v(x) определяем u(x) как реш-е ур-я  . тогда
. тогда  . отсюда реш-е линейного неоднородного ур-я сводится к реш-ю двух ур-ей с раздедяющимися переменными и имеет вид
. отсюда реш-е линейного неоднородного ур-я сводится к реш-ю двух ур-ей с раздедяющимися переменными и имеет вид 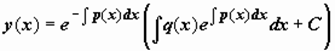 .
.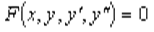
 . Уравнение
. Уравнение  будем называть линейным неоднородным уравнением.
будем называть линейным неоднородным уравнением. называется уравнением с постоянными коэффициентами и записывают его так:
называется уравнением с постоянными коэффициентами и записывают его так:  . Для нахождения y1(x), y2(x)этого ур-я при f(x)=0 составляет квадратноеур-е λ2λ+pλ+q=0, кот-е назыв. характеристическим.
. Для нахождения y1(x), y2(x)этого ур-я при f(x)=0 составляет квадратноеур-е λ2λ+pλ+q=0, кот-е назыв. характеристическим.
 где а,м? R, а,м =соnst
где а,м? R, а,м =соnst если «м» не явл корнем Ур-я к²+pк+q=0
если «м» не явл корнем Ур-я к²+pк+q=0 если «м» –простой корень ур-я к²+pк+q=0
если «м» –простой корень ур-я к²+pк+q=0 если «м»-кратный корень Ур-я к²+pк+q=0
если «м»-кратный корень Ур-я к²+pк+q=0 называется числовым рядом. Числа u1, u2,…,un,… называются первым, вторым, …, n- м, … членами ряда. un также называется общим членом ряда.
называется числовым рядом. Числа u1, u2,…,un,… называются первым, вторым, …, n- м, … членами ряда. un также называется общим членом ряда.

 то он называется суммой ряда, а ряд называется сходящимся. Если
то он называется суммой ряда, а ряд называется сходящимся. Если 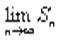 не существует или равен бесконечности, то ряд называется расходящимся и суммы не имеет. Разность rn между его суммой S и частичной суммой Sn: rn=S- Sn называют остатком ряда после n-го члена или n-ым остатком ряда. Подробнее,
не существует или равен бесконечности, то ряд называется расходящимся и суммы не имеет. Разность rn между его суммой S и частичной суммой Sn: rn=S- Sn называют остатком ряда после n-го члена или n-ым остатком ряда. Подробнее, 
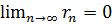
 = 0.
= 0. = S. Тогда имеет место также равенство
= S. Тогда имеет место также равенство  = S, так как при n
= S, так как при n 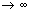 и (n-1)
и (n-1)  -
-  =
=  =
= 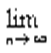 un =0, что и требовалось доказать.
un =0, что и требовалось доказать. un =0 не следует, что ряд сходится.
un =0 не следует, что ряд сходится.

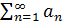 и
и  сходятся, то сумма этих числ рядов также явл сход числовым рядом, при этом его сумма равна сумме исходных рядов:
сходятся, то сумма этих числ рядов также явл сход числовым рядом, при этом его сумма равна сумме исходных рядов:  =
= 

 , a1≠0, q≠1
, a1≠0, q≠1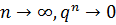 (так как | q |<1), поэтому
(так как | q |<1), поэтому 
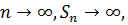 Таким образом, ряд расходящийся.
Таким образом, ряд расходящийся. частичные суммы
частичные суммы  стремятся ни к какому пределу. Ряд расходится
стремятся ни к какому пределу. Ряд расходится
 и, следовательно,
и, следовательно,  , поэтому ряд является расходящимся и суммы не имеет
, поэтому ряд является расходящимся и суммы не имеет называется гармоническим. Можно строго сказать, что он расходится.
называется гармоническим. Можно строго сказать, что он расходится. , где α – любое действительное число.
, где α – любое действительное число.

 расходится, то расходится и ряд
расходится, то расходится и ряд  ≠0, то ряды сходятся или расходятся одновременно. В качестве этал – ряд Дирихле.
≠0, то ряды сходятся или расходятся одновременно. В качестве этал – ряд Дирихле. . При l <1 ряд сходится, при l >1 ряд расходится. Если l =1, то признак не дает ответ
. При l <1 ряд сходится, при l >1 ряд расходится. Если l =1, то признак не дает ответ


 (19)
(19)

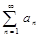 , содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, наз-ся знакопеременным.
, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, наз-ся знакопеременным.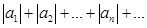 сх-ся, то ряд
сх-ся, то ряд  наз абсолютно сходящимся.
наз абсолютно сходящимся.

 - ряд из абсол значений величин.Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно.
- ряд из абсол значений величин.Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно. (19)
(19)
 (1)
(1)

 сх-ся, то ряд
сх-ся, то ряд  наз абсолютно сходящимся.
наз абсолютно сходящимся.
 - ряд из абсол значений величин
- ряд из абсол значений величин , где
, где  - числа, называемые коэффициентами ряда, x – переменная, наз-ся степенным рядом. Интервал (-R;R) наз интервалом сх-ти степ ряда. Заметим, что для x?(-R;R) ряд сходится абсолютно, а в точках x= ± R степенной ряд может сходиться или расходиться. Для нахождения радиуса сходимости можно воспольз-ся, признаками Даламбера или Коши. Теорема. Если существует
- числа, называемые коэффициентами ряда, x – переменная, наз-ся степенным рядом. Интервал (-R;R) наз интервалом сх-ти степ ряда. Заметим, что для x?(-R;R) ряд сходится абсолютно, а в точках x= ± R степенной ряд может сходиться или расходиться. Для нахождения радиуса сходимости можно воспольз-ся, признаками Даламбера или Коши. Теорема. Если существует  | an+1/ an|=L, то R=1/L=
| an+1/ an|=L, то R=1/L= 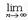 | an/ an+1|. (Док-во. Рассмотрим ряд
| an/ an+1|. (Док-во. Рассмотрим ряд  anxn. Применим к нему признак Даламбера.
anxn. Применим к нему признак Даламбера.  | an+1xn+1/ anxn|=
| an+1xn+1/ anxn|=  | an+1/ an|∙| x | =L∙| x |. Отсюда следует, что если L∙| x |<1, т,е. если | x |<1/L, то ряд сходится абсолютно. Если L∙| x |>1, то ряд расходится. Теорема доказана.) Заметим, что если L=0, для любого | x | то R=∞. Если L=∞, для любого x≠0, то R=0. Если R=0, то ряд сходится в единственной точке x0=0; если R=∞, то ряд сходится на всей числовой прямой. Итак, интервал сходимости ряда
| an+1/ an|∙| x | =L∙| x |. Отсюда следует, что если L∙| x |<1, т,е. если | x |<1/L, то ряд сходится абсолютно. Если L∙| x |>1, то ряд расходится. Теорема доказана.) Заметим, что если L=0, для любого | x | то R=∞. Если L=∞, для любого x≠0, то R=0. Если R=0, то ряд сходится в единственной точке x0=0; если R=∞, то ряд сходится на всей числовой прямой. Итак, интервал сходимости ряда  anxn есть (-R;R). Для нахождения области сходимости ряда надо отдельно исследовать сходимость в точках x=R и x=-R; в зав-ти от рез-тов этого исслед-я обл-ю сх-ти ряда м. б. один из промежутков: [-R;R],(-R;R),[-R;R),(-R;R]. Теорема Абеля: 1) Если степенной ряд
anxn есть (-R;R). Для нахождения области сходимости ряда надо отдельно исследовать сходимость в точках x=R и x=-R; в зав-ти от рез-тов этого исслед-я обл-ю сх-ти ряда м. б. один из промежутков: [-R;R],(-R;R),[-R;R),(-R;R]. Теорема Абеля: 1) Если степенной ряд  anxn сходится при x=x0, то он сходится причем абсолютно для всех x, удовлетворяющих неравенству |x|<|x0|. 2) Если же ряд
anxn сходится при x=x0, то он сходится причем абсолютно для всех x, удовлетворяющих неравенству |x|<|x0|. 2) Если же ряд 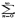 anxn расходится при x=x1, то он расходится при всех x, удовлетворяющих условию |x|>|x1|. (Док-во 1)Так как числовой ряд
anxn расходится при x=x1, то он расходится при всех x, удовлетворяющих условию |x|>|x1|. (Док-во 1)Так как числовой ряд  anx0n сходится, то
anx0n сходится, то 
 anx0n=0. Это означает, что числовая последовательность {anx0n} ограничена.Тогда перепишем степенной ряд в виде a0 + a1x0 (x/x0) + a2x02(x2/x02) +…+…=
anx0n=0. Это означает, что числовая последовательность {anx0n} ограничена.Тогда перепишем степенной ряд в виде a0 + a1x0 (x/x0) + a2x02(x2/x02) +…+…=  anx0n (x/x0)2. Рассмотрим ряд из абсолютных величин. |a0| + |a1x0 (x/x0) | + |a2x02(x2/x02) | +…+…<= M + M| x/x0| + M| x/x0|2 +…= M(1+q+ q2+…). Это геометрическая прогрессия с q=(x/x0)<1—сходится. Из признака сравнения следует абсолютная сходимость степенного ряда. 2)От противного. Пусть степенной ряд сходится при некотором x*, | x*|> x1. Но тогда согласно 1-ой части теоремы, степенной ряд сходится для всех | x |< x*. В том числе должен сходится и при x= x0, так как | x |< | x*|. Но это противоречит предположению теоремы. Теорема доказана.)
anx0n (x/x0)2. Рассмотрим ряд из абсолютных величин. |a0| + |a1x0 (x/x0) | + |a2x02(x2/x02) | +…+…<= M + M| x/x0| + M| x/x0|2 +…= M(1+q+ q2+…). Это геометрическая прогрессия с q=(x/x0)<1—сходится. Из признака сравнения следует абсолютная сходимость степенного ряда. 2)От противного. Пусть степенной ряд сходится при некотором x*, | x*|> x1. Но тогда согласно 1-ой части теоремы, степенной ряд сходится для всех | x |< x*. В том числе должен сходится и при x= x0, так как | x |< | x*|. Но это противоречит предположению теоремы. Теорема доказана.) с областью сходимости (-R;R). Тогда сумма S(x) явл дифференцируемой функцией в инт (-R;R). Ее произв S'(x)=
с областью сходимости (-R;R). Тогда сумма S(x) явл дифференцируемой функцией в инт (-R;R). Ее произв S'(x)= 
 (-R;R).
(-R;R).



