
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные уравнения первого порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
№4. Найти общее решение уравнения (х+у) dx–xdy= 0. Решение. Данное уравнение является однородным уравнением первой степени относительно переменных х и у. Действительно, P (λx, λy) =λx+λy=λ (x+y) = λP (x,y), Q (λx, λy) = –λx=λ (–x) =λQ (x, y). Положим у=uх, где u – новая функция от х. Найдем дифференциал произведения: dy=хdu+udх. Подставив выражение у и dy в данное уравнение, получим (х+uх) dх–х (хdu+udх) = 0, откуда хdх + uхdх–х 2 du–хudх= 0; х dх–х 2 du= 0 или dх–хdu= 0. Таким образом, получили уравнение с разделяющимися переменными. Разделив переменные и интегрируя, находим
Заменяя в полученном выражении u на Отметим, что заданное уравнение можно было сначала привести к виду (9.3.2):
№5. Найти общее решение уравнения: Решение. Это однородное уравнение третьей степени. Преобразуем его к виду (10.6):
Полагая у = uх, находим
Подставим теперь Итак, общее решение исходного уравнения №6. Найти частное решение уравнения Решение. Перепишем уравнение в виде х 2 dy = (xy + y 2 ) dx (*) и воспользуемся подстановкой у=uх. Тогда dy= udх+ хdu. Подставив выражение у и dy в уравнение (*), имеем х 2 (udх + хdu) = (х.uх+u 2 х 2 ) dх; x 2 (udx+xdu) =x 2 (u+u 2 ) dx; udx+xdu= udx+ u 2 dx; т.е. xdu= u 2 dx. Получили уравнение с разделяющимися переменными. Разделив переменные и интегрируя, получим
Так как u = Используя начальные условия х =1, у = –1,имеем1=ln1 + C, откуда С =1. Следовательно,
Отсюда получаемискомое частное решение данного уравнения №7. Привести дифференциальное уравнение
Решение. Иначе это уравнение можно записать так (u+ (β+ 2 )) du –( 2 u+v+ ( 2 α+β+ 6 )) dv= 0. Подберем α и β так, чтобы α= – 2, β= – 2. Тогда данное уравнение преобразуется к виду (10.5): Линейные уравнения первого порядка №8. Решить уравнение
Решение. Здесь P (x)=– ctg x, Q (x) = sin x. Решим уравнение двумя методами.
I. Метод Лагранжа Найдем сначала общее решение соответствующего ЛОДУ
Отсюда Общее решение ЛНДУ ищем в виде Найдем Подставим у и
Получили Следовательно, общее решение исходного уравнения есть y= (x+C) sin x. II. Метод Бернулли Пусть
или
Подберем функцию u (x) так, чтобы выражение в скобках равнялось нулю, т.е. решим первое дифференциальное уравнение с разделяющимися переменными
Откуда u=С 1 × sin x. Пусть С 1=1, u= sin x.
Итак, y= (x+C)· sin x, №9. Найти общее решение уравнения Решение. Данное уравнение не является линейным относительно х и
Метод вариации произвольной постоянной Найдем сначала общее решение соответствующего ЛОДУ Общее решение ЛОДУ можно записать так х= Су, Общее решение заданного (преобразованного) уравнения ищем в виде х=С (у) у (постоянную С заменили неизвестной функцией С (у)). Подставляя х и
Отсюда Таким образом, общее решение ЛНДУ есть х = (у + С) у или х = у 2 + Су. Заметим, что у = 0 также является решением, и для нашего примера оно является особым.
Метод подстановки Полагаем
Решим дифференциальное уравнение с разделяющимися переменными
откуда v=Cy, Выбираем одно из частных решений (самое простое), например, при С = 1, т. е. v = y. Подставив v = y в уравнение (*), получим
Варианты заданий Уравнения с разделяющимися переменными №10.1. Найти общие интегралы (общие решения) уравнений. а) б) в) г) д) е) ж) з) и) к) №10.2. Найти частные решения уравнений, удовлетворяющие указанным начальным условиям:
а) б) в) г) д) е) ж) з) и) к)
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1020; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.253 (0.012 с.) |

 ,
,  .
. , получим у=x ln (Cx). Это и есть общее решение данного уравнения.
, получим у=x ln (Cx). Это и есть общее решение данного уравнения. . Иначе
. Иначе  . Далее применять указанную выше подстановку и т.д.
. Далее применять указанную выше подстановку и т.д. .
.
 Подставим значения
Подставим значения  в данное уравнение:
в данное уравнение:  . Преобразовывая, получим уравнение с разделяющимися переменными
. Преобразовывая, получим уравнение с разделяющимися переменными  . Разделяя переменные и интегрируя, находим:
. Разделяя переменные и интегрируя, находим: .
.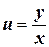 в полученное решение. Имеем
в полученное решение. Имеем  где
где 
 если у=– 1 при х= 1.
если у=– 1 при х= 1. .
. .
. ,
,  .
. к однородному.
к однородному.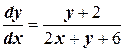 . Здесь
. Здесь 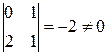 , поэтому положив x=u+α, y=v+β, получаем (u+β+ 2 ) du– ( 2 u+ 2 α+v+β+ 6 ) dv= 0, т. е.
, поэтому положив x=u+α, y=v+β, получаем (u+β+ 2 ) du– ( 2 u+ 2 α+v+β+ 6 ) dv= 0, т. е.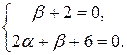 Решая систему, находим
Решая систему, находим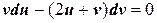 , т.е. является однородным.
, т.е. является однородным. .
. , т.е.
, т.е. 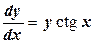 . Предположим, что
. Предположим, что  (у =0 – решение данного уравнения), разделяя переменные и интегрируя, получим
(у =0 – решение данного уравнения), разделяя переменные и интегрируя, получим ,
,  ,
, .
. .
. .
. в исходное уравнение:
в исходное уравнение: или
или  .
. или
или  . Тогда
. Тогда  .
. . Тогда
. Тогда  и уравнение принимает вид
и уравнение принимает вид ,
, .
. ,
,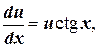
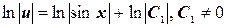 .
. , отсюда
, отсюда 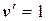 , т.е.
, т.е.  .
. есть общее решение данного ЛНДУ.
есть общее решение данного ЛНДУ.
 . Так как
. Так как  , то приведем исходное уравнение к виду (10.6):
, то приведем исходное уравнение к виду (10.6):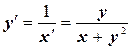 , т.е.
, т.е.  или
или  Далее это ДУ решим двумя методами:
Далее это ДУ решим двумя методами: Разделяя переменные и интегрируя, получим ln | x | = ln | y | + ln | C 1|, C 1
Разделяя переменные и интегрируя, получим ln | x | = ln | y | + ln | C 1|, C 1  .
. (так как х= 0 – решение).
(так как х= 0 – решение). в ЛНДУ, придем к равенству:
в ЛНДУ, придем к равенству: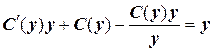 , т.е.
, т.е.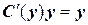 .
. . Интегрируя, имеем С (у) = у + С.
. Интегрируя, имеем С (у) = у + С. , где u=u (y), v=v (y) – функции переменной у. Подставим х и
, где u=u (y), v=v (y) – функции переменной у. Подставим х и  в уравнение
в уравнение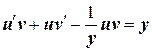 или
или . (*)
. (*)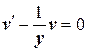 ,
,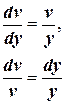
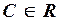 .
.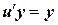 или
или  . Тогда u = у + С. Следовательно, общее решение заданного уравнения х = у 2 + Су,
. Тогда u = у + С. Следовательно, общее решение заданного уравнения х = у 2 + Су,  , при этом у = 0 – особое решение.
, при этом у = 0 – особое решение. ;
; ;
;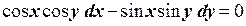 ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
;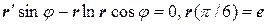 ;
;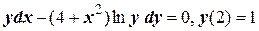 ;
;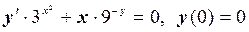 ;
; ;
; ;
; ;
; ;
; ;
; .
.


