
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения второго порядкаСодержание книги
Поиск на нашем сайте
Задача 6. Дано уравнение:
Решение:
Данное дифференциальное уравнение второго порядка не содержит явно функцию
откуда
Определим численное значение
Определим численное значение Таким образом, Задача 7. Дано уравнение Решение:
Данное уравнение второго порядка не содержит явно аргумента Если
Если приравнять нулю первый множитель, то получаем:
Приравняем нулю второй множитель:
Используя начальные условия, находим
Далее решаем уравнение
Теперь определим значение
Тогда
Задача 8. Найти частные решения неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами со специальной правой частью, удовлетворяющее указанным начальным условиям: а) б)
Решение:
При решении данных уравнений удобно использовать следующий алгоритм. Если дано неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами со специальной правой частью 1. Чтобы найти 1) уравнение имеет действительные различные корни 2) уравнение имеет действительные равные корни 3) уравнение имеет комплексные корни 2. Если правая часть уравнения При составлении частного решения
Решение:
а) Общее решение данного уравнения имеет вид: Найдём Теперь найдём Получаем:
Запишем
Далее приравниваем коэффициенты при соответствующих степенях
Тогда Подставляем начальные условия
Тогда б) Общее решение данного уравнения имеет вид: Найдём Теперь найдём Рассмотрим Получаем: Рассмотрим Получаем:
Тогда
Далее приравниваем коэффициенты при соответствующих подобных слагаемых:
Тогда
Тогда Ряды и их приложения Задача 9. Вычислить интеграл
Решение:
Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд Маклорена функции sinx, имеем:
Мы получили знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в полученном ряде четвертый член по абсолютному значению меньше 0,001, то ограничиваемся только первыми тремя членами.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.223 (0.008 с.) |

 . Найти частное решение, удовлетворяющее начальным условиям:
. Найти частное решение, удовлетворяющее начальным условиям:  ;
;  .
. . Положим
. Положим 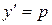 , где
, где  – некоторая функция аргумента
– некоторая функция аргумента  . Если
. Если  и данное уравнение примет вид
и данное уравнение примет вид 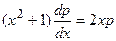 . Мы получили уравнение первого порядка относительно переменных
. Мы получили уравнение первого порядка относительно переменных  ;
;  ;
; ,
, или
или  .
. при указанных начальных условиях. Имеем
при указанных начальных условиях. Имеем 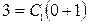 . Следовательно,
. Следовательно,  . Теперь решаем уравнение первого порядка
. Теперь решаем уравнение первого порядка  :
: ;
;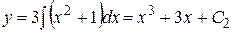 .
. при указанных начальных условиях. Имеем
при указанных начальных условиях. Имеем  ;
;  .
. есть частное решение, удовлетворяющее указанным начальным условиям.
есть частное решение, удовлетворяющее указанным начальным условиям.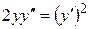 . Найти частное решение, удовлетворяющее начальным условиям:
. Найти частное решение, удовлетворяющее начальным условиям:  ;
;  .
. . Положим
. Положим  .
. . Тогда данное уравнение примет вид
. Тогда данное уравнение примет вид ;
;  ;
;  .
. ;
;  ;
; 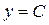 – решение данного уравнения.
– решение данного уравнения. ;
;  ;
;  ;
; или
или  .
. :
: ;
;  .
.
 :
: ;
; 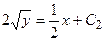 .
. :
: ;
;  .
. ;
;  и
и  – искомое частное решение, удовлетворяющее указанным начальным условиям.
– искомое частное решение, удовлетворяющее указанным начальным условиям.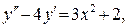
 ;
;
 .
. где
где 
 , где
, где  – многочлен степени
– многочлен степени  ,
,  – многочлен степени
– многочлен степени  . Тогда общее решение уравнения ищется в виде
. Тогда общее решение уравнения ищется в виде  , где
, где  – общее решение соответствующего однородного уравнения,
– общее решение соответствующего однородного уравнения, 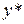 – какое-либо частное решение неоднородного уравнения.
– какое-либо частное решение неоднородного уравнения. составляем характеристическое уравнение
составляем характеристическое уравнение  , при решении которого возможны следующие случаи:
, при решении которого возможны следующие случаи: , тогда
, тогда  , где
, где  и
и  - произвольные постоянные;
- произвольные постоянные; , тогда
, тогда  , где
, где  и
и 
 , тогда
, тогда  , где
, где  имеет специальный вид
имеет специальный вид 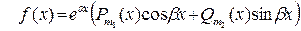 , где
, где  – многочлен степени
– многочлен степени  ,
,  и
и  – многочлены степени
– многочлены степени  ,
,  , а
, а  – кратность корня
– кратность корня 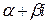 характеристического уравнения
характеристического уравнения  =0
=0







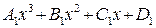
 .
. . Составляем характеристическое уравнение:
. Составляем характеристическое уравнение:  . Корнями этого уравнения являются
. Корнями этого уравнения являются  и
и  . Т.к. решения действительные различные числа (первый случай), то
. Т.к. решения действительные различные числа (первый случай), то  или
или 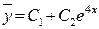 .
. имеет специальный вид, причём
имеет специальный вид, причём 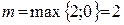 ,
,  =0,
=0,  =0, тогда
=0, тогда  и
и  , так как
, так как  ,
,  =1,
=1,  =0, то
=0, то  ,
, . Найдём производные первого и второго порядка от
. Найдём производные первого и второго порядка от  ,
, 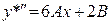 .
. и
и  следующим образом, подписывая слева коэффициенты
следующим образом, подписывая слева коэффициенты  и
и  из исходного уравнения:
из исходного уравнения:



 . Следовательно, общее решение исходного уравнения:
. Следовательно, общее решение исходного уравнения:  . Чтобы найти частное решение, удовлетворяющее начальным условиям, найдём
. Чтобы найти частное решение, удовлетворяющее начальным условиям, найдём  .
.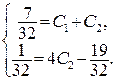 отсюда
отсюда 
 – частное решение исходного уравнения.
– частное решение исходного уравнения. . Составляем характеристическое уравнение:
. Составляем характеристическое уравнение: 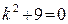 ,
,  . Корнями этого уравнения являются
. Корнями этого уравнения являются  и
и  . Так как решения комплексные числа (третий случай), то
. Так как решения комплексные числа (третий случай), то  или
или  .
.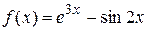 есть сумма двух функций, имеющих специальный вид:
есть сумма двух функций, имеющих специальный вид:  , где
, где  и
и  . Тогда
. Тогда 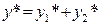 .
. ,
,  не совпадает ни с одним из корней характеристического уравнения, т.о.
не совпадает ни с одним из корней характеристического уравнения, т.о.  =0.
=0. , т.к.
, т.к.  ,
,  =1,
=1,  .
. ,
,  не совпадает ни с одним из корней характеристического уравнения, таким образом
не совпадает ни с одним из корней характеристического уравнения, таким образом  =0.
=0.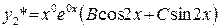 , так как
, так как  =1, то
=1, то .
.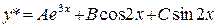 . Найдём производные первого и второго порядка от
. Найдём производные первого и второго порядка от  ,
,  . Запишем
. Запишем  следующим образом, подписывая слева коэффициенты
следующим образом, подписывая слева коэффициенты 
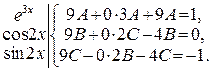


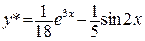 . Следовательно, общее решение исходного уравнения:
. Следовательно, общее решение исходного уравнения:  . Чтобы найти частное решение, удовлетворяющее начальным условиям, найдём
. Чтобы найти частное решение, удовлетворяющее начальным условиям, найдём  . Подставляем начальные условия
. Подставляем начальные условия 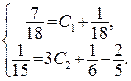 отсюда
отсюда 
 - частное решение исходного уравнения.
- частное решение исходного уравнения. с точностью до 0,001.
с точностью до 0,001. , тогда
, тогда 






