
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральные уравнения Вольтера 2-ого родаСодержание книги
Поиск на нашем сайте
Интегральные уравнения Вольтера 2-ого рода Линейным интегральным уравнением Вольтера 2-ого рода называется уравнение
где Решением уравнения (1) называется всякая функция Интегральные уравнения Вольтерра 2-ого рода используются обычно при описании динамики различных процессов в системах. В частности, всякая задача Коши для линейного дифференциального уравнения
может быть сведена к решению некоторого линейного интегрального уравнения Вольтерра 2-ого рода. Задача Коши для произвольного дифференциального уравнения 1 – ого порядка вида
эквивалентна в общем случае нелинейному интегральному уравнению Вольтерра
Аналогично, задача Коши для произвольного дифференциального уравнения n – ого порядка, разрешенного относительно старшей производной
может быть сведена к системе нелинейных интегральных уравнений Вольтерра. Во многих случаях решение интегрального уравнения Вольтера 2-ого рода (или системы таких уравнений) в свою очередь может быть сведено к решению некоторой задачи Коши для обыкновенных дифференциальных уравнений. Рассмотрим два способа, посредством которых это может быть сделано. а) Если в исходном интегральном уравнении (1) ядро Рассмотренный прием всегда приводит к цели в том случае, когда ядро Пусть исходное интегральное уравнение (1) имеет вид
(уравнение с вырожденным ядром). Запишем его следующим образом:
Вводя функции
¼¼¼¼¼¼¼¼¼¼¼ (16)
и подставляя их в (15), заключаем, что решение интегрального уравнения (14) имеет вид
Далее, дифференцируя соотношения (16) и подставляя вместо
¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼
Из (16) при Метод последовательных приближений. Метод последовательных приближений применительно к линейному интегральному уравнению Вольтера 2-ого рода
заключается в следующем. Строится последовательность функций
Если ядро Обычно полагают Теоремы Фредгольма. Для уравнений Фредгольма 2-ого рода вида
где 1. Однородное уравнение
имеет либо конечное, либо счетное множество характеристических чисел; если этих чисел счетное множество, то они стремятся к бесконечности. 2. Если l - характеристическое число, то уравнение (29) и сопряженное ему однородное уравнение
где 3. Альтернатива Фредгольма: либо неоднородное уравнение (28) имеет одно и только одно решение для любой функции 4. Если l - характеристическое число, то для того чтобы уравнение (28) имело решение, необходимо и достаточно, чтобы свободный член
Проиллюстрируем теоремы Фредгольма на примере интегрального уравнения с вырожденным ядром. Вариация функционала. Для любой Рассмотрим приращение функционала в произвольной внутренней «точке»
Если в приращении функционала можно выделить линейную часть по отношению к вариации
где Рассмотрим однопараметрическое семейство функций
где
Первую вариацию также называют дифференциалом Гато (Гатó Рене Эжен – французский математик). Заметим, что из дифференцируемости по Фреше функционала I следует существование его первой вариации, которая в этом случае совпадает с дифференциалом, то есть Изопериметрические задачи Изопериметрическими задачами называются задачи, в которых рассматриваются функционалы вида
с граничными условиями
и так называемыми параметрическими условиями,
Изопериметрическая задача может быть сведена к задаче на безусловный экстремум функционал
Уравнения Эйлера для функционала
Из последних
следовательно, получаем следующее правило: Для получения основного необходимого условия в изопериметрической задаче о нахождении экстремума функционала
Примечание. Материалы данного справочника ни в коем случае не являются самостоятельным учебным материалом: все приведенные теоремы необходимо дополнить доказательствами (если другое не оговорено здесь), а используемые понятия - дополнительными пояснениями, изложенными в лекционном курсе или учебниках по соответствующим разделам. Интегральные уравнения Вольтера 2-ого рода Линейным интегральным уравнением Вольтера 2-ого рода называется уравнение
где Решением уравнения (1) называется всякая функция Интегральные уравнения Вольтерра 2-ого рода используются обычно при описании динамики различных процессов в системах. В частности, всякая задача Коши для линейного дифференциального уравнения
может быть сведена к решению некоторого линейного интегрального уравнения Вольтерра 2-ого рода. Задача Коши для произвольного дифференциального уравнения 1 – ого порядка вида
эквивалентна в общем случае нелинейному интегральному уравнению Вольтерра
Аналогично, задача Коши для произвольного дифференциального уравнения n – ого порядка, разрешенного относительно старшей производной
может быть сведена к системе нелинейных интегральных уравнений Вольтерра. Во многих случаях решение интегрального уравнения Вольтера 2-ого рода (или системы таких уравнений) в свою очередь может быть сведено к решению некоторой задачи Коши для обыкновенных дифференциальных уравнений. Рассмотрим два способа, посредством которых это может быть сделано. а) Если в исходном интегральном уравнении (1) ядро Рассмотренный прием всегда приводит к цели в том случае, когда ядро Пусть исходное интегральное уравнение (1) имеет вид
(уравнение с вырожденным ядром). Запишем его следующим образом:
Вводя функции
¼¼¼¼¼¼¼¼¼¼¼ (16)
и подставляя их в (15), заключаем, что решение интегрального уравнения (14) имеет вид
Далее, дифференцируя соотношения (16) и подставляя вместо
¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼
Из (16) при
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 967; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.94.112 (0.006 с.) |

 , (1)
, (1) - искомая функция,
- искомая функция,  и
и  - известные функции, определенные соответственно в треугольнике
- известные функции, определенные соответственно в треугольнике  и на отрезке
и на отрезке  . Функция
. Функция  , подстановка которой в это уравнение обращает его в тождество. Вопрос о существовании и единственности решения решается различным образом в зависимости от свойства ядра
, подстановка которой в это уравнение обращает его в тождество. Вопрос о существовании и единственности решения решается различным образом в зависимости от свойства ядра 
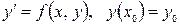
 .
.
 и
и  , то это уравнение может быть продифференцировано (один или несколько раз), что и позволяет в ряде случаев свести его к задаче Коши для некоторого обыкновенного дифференциального уравнения.
, то это уравнение может быть продифференцировано (один или несколько раз), что и позволяет в ряде случаев свести его к задаче Коши для некоторого обыкновенного дифференциального уравнения. .
. (14)
(14) . (15)
. (15) ,
,
 . (17)
. (17) систему дифференциальных уравнений
систему дифференциальных уравнений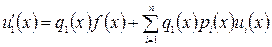 ,
, находим начальные условия:
находим начальные условия:  . Определив функции
. Определив функции 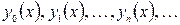 , где нулевое приближение
, где нулевое приближение  - произвольная функция, а последующие приближения определяются с помощью рекуррентного соотношения
- произвольная функция, а последующие приближения определяются с помощью рекуррентного соотношения
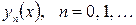 при
при  сходится к единственному непрерывному решению интегрального уравнения.
сходится к единственному непрерывному решению интегрального уравнения.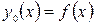 , однако это вовсе не обязательно: удачный выбор нулевого приближения часто позволяет ускорить сходимость последовательности
, однако это вовсе не обязательно: удачный выбор нулевого приближения часто позволяет ускорить сходимость последовательности  к точному решению.
к точному решению. , (28)
, (28)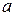 и
и  - конечные числа, а ядро
- конечные числа, а ядро  и на отрезке
и на отрезке  (29)
(29) , (30)
, (30) , имеют одно и то же, и притом конечное, число линейно независимых решений.
, имеют одно и то же, и притом конечное, число линейно независимых решений. , либо соответствующее однородное уравнение (29) имеет, по крайней мере, одно нетривиальное решение. (Другими словами, если число l не является характеристическим, то уравнение (28) имеет, и притом единственное, решение для любой функции
, либо соответствующее однородное уравнение (29) имеет, по крайней мере, одно нетривиальное решение. (Другими словами, если число l не является характеристическим, то уравнение (28) имеет, и притом единственное, решение для любой функции 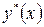 однородного сопряженного уравнения (30), т.е.
однородного сопряженного уравнения (30), т.е. .
. разность
разность  называют вариацией функции
называют вариацией функции 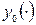 ; здесь
; здесь  . Таким образом, вариация функции сама является функцией из того же пространства, то есть
. Таким образом, вариация функции сама является функцией из того же пространства, то есть 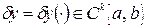 . Будем говорить, что «точка»
. Будем говорить, что «точка»  является внутренней для множества D, если она входит в него вместе с некоторой своей d – окрестностью.
является внутренней для множества D, если она входит в него вместе с некоторой своей d – окрестностью.
 .
. , то есть представить
, то есть представить ,
, – линейный функционал относительно
– линейный функционал относительно  – величина, имеющая более высокий порядок малости, чем
– величина, имеющая более высокий порядок малости, чем  , то линейная часть
, то линейная часть  , а функционал считается дифференцируемым по Фреше (Фрешé Морис Рене – французский математик).
, а функционал считается дифференцируемым по Фреше (Фрешé Морис Рене – французский математик). ,
, – параметр,
– параметр, 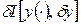 функционала I в «точке»
функционала I в «точке» 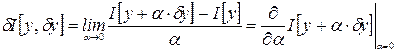 .
.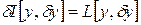 . Однако существование первой вариации функционала I еще не означает его дифференцируемости в соответствующей «точке»
. Однако существование первой вариации функционала I еще не означает его дифференцируемости в соответствующей «точке»  (1)
(1) ,
,  (2)
(2) - числа
- числа 
 . (3)
. (3)
 .
.


 уравнений получаем, что
уравнений получаем, что  - постоянные, а первые
- постоянные, а первые  уравнений совпадут с уравнениями Эйлера для функционала
уравнений совпадут с уравнениями Эйлера для функционала (4),
(4), при наличии связей (3), надо составить вспомогательный функционал (4), где
при наличии связей (3), надо составить вспомогательный функционал (4), где 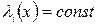 и написать для него уравнение Эйлера. Произвольные постоянные
и написать для него уравнение Эйлера. Произвольные постоянные  в общем решении уравнения Эйлера и постоянные
в общем решении уравнения Эйлера и постоянные  определяются из граничных условий (2) и изопериметрических условий (3).
определяются из граничных условий (2) и изопериметрических условий (3).


