
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функционалы, зависящие от производных более высоких порядков.Содержание книги
Поиск на нашем сайте
Рассматривается функционал В этом случае получаем, что экстремаль
– уравнение Эйлера – Пуассона. Уравнение (1) представляет собой обыкновенное дифференциальное уравнение, порядка Простейшая задача с подвижными концами. Предположим, что в простейшей задаче правая граничная точка допустимых кривых не закреплена, то есть отсутствует условие
Из необходимого условия экстремума после соответствующих преобразований следует
Могут быть две различные ситуации: 1. Если правый конец свободный, 2. Если правый конец экстремали должен быть расположен на заданной кривой
– условие трансверсальности. Здесь возможны также частные ситуации: а) Аналогично, получаем условия на левом конце. Вариационные задачи на условный экстремум. Случай геометрических и дифференциальных связей. Задачей на условный экстремум называется задача на экстремум, в которой накладываются дополнительные ограничения в виде уравнений, связывающих переменные Связи вида Это геометрические связи, они не содержат производных независимых функций. Задача на условный экстремум в этом случае имеет вид:
Из (1), (3) составим вспомогательный функционал
Теорема. Функции Уравнение Замечание. Уравнения Связи вида ( входят также производные неизвестных функций – так называемые дифференциальные связи ) Пусть требуется отыскать экстремум функционала
при дополнительных условиях
– неголономные (дифференциальные) связи. Здесь так же можно доказать правило множителей, заключающееся в том, что условный экстремум функционала
Таким образом, функции
то есть должны удовлетворять уравнениям Эйлера для вспомогательного функционала Изопериметрические задачи Изопериметрическими задачами называются задачи, в которых рассматриваются функционалы вида
с граничными условиями
и так называемыми параметрическими условиями,
Изопериметрическая задача может быть сведена к задаче на безусловный экстремум функционал
Уравнения Эйлера для функционала
Из последних
следовательно, получаем следующее правило: Для получения основного необходимого условия в изопериметрической задаче о нахождении экстремума функционала
Примечание. Материалы данного справочника ни в коем случае не являются самостоятельным учебным материалом: все приведенные теоремы необходимо дополнить доказательствами (если другое не оговорено здесь), а используемые понятия - дополнительными пояснениями, изложенными в лекционном курсе или учебниках по соответствующим разделам.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.133.251 (0.01 с.) |

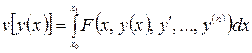 с граничными условиями
с граничными условиями 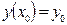 ,
, 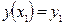 ,
, 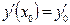 ,
,  , …,
, …,  ,
,  .
. должна удовлетворять уравнению
должна удовлетворять уравнению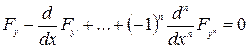 (1)
(1)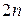 общее решение содержит
общее решение содержит 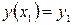 , и задача принимает вид:
, и задача принимает вид: , (1)
, (1)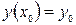 . (2)
. (2)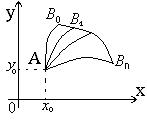 Надо найти кривую
Надо найти кривую 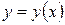 , проходящую через точку
, проходящую через точку 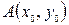 и доставляющую экстремум функционалу (1). Будем исходить из того, что искомая кривая должна быть экстремалью, то есть удовлетворять уравнению Эйлера
и доставляющую экстремум функционалу (1). Будем исходить из того, что искомая кривая должна быть экстремалью, то есть удовлетворять уравнению Эйлера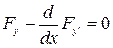 (3)
(3)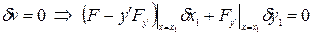 . (4)
. (4)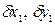 - независимые. (4) выполняется при любых
- независимые. (4) выполняется при любых 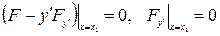 , или
, или  .
.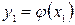 , тогда
, тогда 
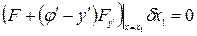 ,
,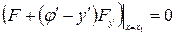 (5)
(5) , тогда
, тогда 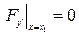 ; б)
; б) 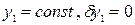 , тогда
, тогда 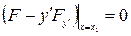 ;
;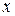 и
и 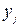 , то есть независимые переменные и неизвестные функции, такие уравнения называются уравнениями связи.
, то есть независимые переменные и неизвестные функции, такие уравнения называются уравнениями связи.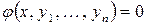 .
. (1)
(1)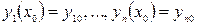 ,
, 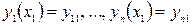 (2)
(2)
 ,
,  (3)
(3)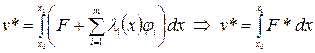 . (4)
. (4)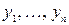 ,реализующие экстремум функционала (1) при наличии условий (3), удовлетворяют при соответствующем выборе множителя
,реализующие экстремум функционала (1) при наличии условий (3), удовлетворяют при соответствующем выборе множителя 
 (4). Функции
(4). Функции  определяются из уравнений Эйлера
определяются из уравнений Эйлера  ,
, 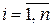 ,
, 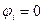 ,
, 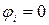 (3)можно так же считать уравнением Эйлера для
(3)можно так же считать уравнением Эйлера для  , если аргументом функционала считать не только
, если аргументом функционала считать не только  отличен от нуля, например
отличен от нуля, например 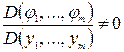 .
.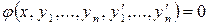 .
. (1)
(1)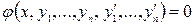 ,
,  достигается на тех же кривых на которых реализуется безусловный экстремум функционала
достигается на тех же кривых на которых реализуется безусловный экстремум функционала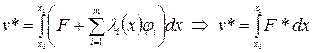 .
.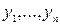 , реализующие экстремум функционала
, реализующие экстремум функционала 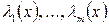 должны удовлетворять
должны удовлетворять 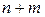 уравнений
уравнений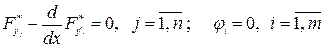 ,
,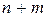 функций
функций 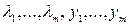 .
. (1)
(1) ,
,  (2)
(2) - числа
- числа  . (3)
. (3) .
.


 уравнений совпадут с уравнениями Эйлера для функционала
уравнений совпадут с уравнениями Эйлера для функционала (4),
(4),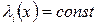 и написать для него уравнение Эйлера. Произвольные постоянные
и написать для него уравнение Эйлера. Произвольные постоянные  в общем решении уравнения Эйлера и постоянные
в общем решении уравнения Эйлера и постоянные  определяются из граничных условий (2) и изопериметрических условий (3).
определяются из граничных условий (2) и изопериметрических условий (3).


