
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разделить коэффициенты уравнения регрессии на параметр, вызывающий гетероскедастичность.Содержание книги
Поиск на нашем сайте
24. Если наличие существенно гетероскедастичности и случайного члена уравнения регрессии ранговой корреляции Спирмена или тестом Голфелда Квандта, то для снижения влияния гетероскедастичнсти на эффективность оценок уравнения регрессии можно каждое наблюдение:
25. Если наличие существенной гетероскедастичности случайного члена уравнения регрессии подтверждено тестом Глейзера то для снижения влияния гетероскедастичности на эффективность оценок уравнения регрессии необходимо: 1) в качестве Zi взять 2) в качестве Zi взять 3)в качестве Zi взять 27. Автокорреляция случайного члена уравнения регрессии – это… Зависимость одного члена уравнения от другого. 2)зависимость всех членов уравнения от случайной компоненты 3)зависимость не включенных в модель факторов. 28. Автокорреляция случайного члена уравнения регрессии приводит к тому, что оценки уравнения регрессии становятся: 1) эффективными, стандартные ошибки коэффициентов регрессии увеличиваются 2)не эффективными, стандартные ошибки коэффициентов регрессии занижаются. 3)отрицательными. 29. Причиной положительной автокорреляции случайного члена уравнения регрессии обычно является: 1) постоянная направленность воздействия включенных в уравнение регрессии каких-либо факторов. 2)увеличение интервала наблюдения. 3)постоянная направленность воздействия не включенного в уравнение регрессии какого-либо фактора
30. Уравнение,отражающее авторегрессионную схему первого порядка для автокорреляции случайного члена, имеет вид: 1)
2)
3)
31. Оценку коэффициента автокорреляции случайного члена уравнения регрессии из авторегрессионной схемы первого порядка можно осуществить по формуле: 1)
2)
3)
32. Расчетное значение d – критерия статистики Дарбина - Уотсона определяется по формуле: 1)
2)
3)
33. Значение d – критерия статистики Дарбина – Уотсона в больших выборках связано с коэффициентом автокорреляции случайного члена уравнения регрессии следующим соотношением: 1) 2) 3)
№ 34 Почему нельзя составить таблицу с указаниями точных критериев значений D критерия статистики Дарбина – Уотсона? 1) Критическое значение DW зависит от количества объясняющих переменных в уравнении регрессии и от количества наблюдений,зависит еще и от конкретных значений, принимаемых объясняющими переменными. 2)т.к. D критерий не зависит от масштаба наблюдений 3) такую таблицу можно составить
№ 35 В каком случае нельзя отключить нулевую гипотезу об отсутствии автокорреляции случайного члена уравнения регрессии? 1) если d<dкрит 2) если d≥dкрит то нельзя отклонить и ошибки будут некоррелированы 3) в любом случае можно
№ 36 По какой формуле пересчитывается значение D критерия статистики Дарбина – Уотсона при отрицательной автокорреляции случайного члена уравнения регрессии? 1) в больших выборках при отрицательной автокорреляции ρ=-1 и dρ≈2-2ρ 2) при отрицательной автокорреляции ρ=1 и dρ≈2-4ρ 3) в больших выборках при отрицательной автокорреляции ρ=0 и dρ≈2-2ρ № 37 Как устранить автокорреляцию случайного члена уравнения регрессии, если она описывается авторегрессионной схемой 1 ого порядка? 1) привести её к виду y’t= α*c + β*x’t + μt 2)методом Кокрана-Оркатта 3)методом Хилдрета -Лу
Для чего используется поправка Прайса-Уинстена? 1) для преобразования модели таким образом, чтобы оценки были несмещенными; 2) для диагностики автокорреляции; 3) для преобразования модели таким образом, чтобы остатки были некоррелированы. 39. Поправка Прайса-Уинстена равна: 1) 2) 3) 40. Для одновременной оценки коэффициента корреляции случайного члена уравнения регрессии и коэффициентов самого уравнения регрессии применяются методы: 1) МНК, КМНК, ДМНК; 2) метод Спирмена, метод Голдфилда-Квандта, метод Глейзера;
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.219.11 (0.006 с.) |

 , пропорциональной
, пропорциональной  ;
; 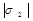 ;
;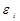 .
.
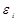

 ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
.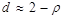 ;
;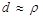 ;
; .
.
 ;
;



