
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Кохрейна-Оркатта, метод Хилдрета-Лу, метод Дарбина.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
41. Метод Кохрейна-Оркатта, используемый для оценки коэффициентов автокорреляции и коэффициентов уравнения регрессии включает следующие этапы: 1) 1. оцениваем исходное регрессионное уравнение, т.е. находим оценки; Вычисляем остатки 3. находим оценку коэффициента автокорреляции 4. используя данную оценку Проводим определение параметров полученного уравнения и находим новые значения оценок Повторно вычисляем остатки и фактически возвращаемся к этапу 3 2) 1. оцениваем исходное регрессионное уравнение, т.е. находим оценки; 2. вычисляем остатки 3. оцениваем адекватность и точность модели; 3) 1. оцениваем исходное регрессионное уравнение, т.е. находим оценки; 2. вычисляем остатки 3. находим d -критерий 4. используя d -критерий определяем наличие автокорреляции 5. находим оценку коэффициента автокорреляции 6. используя данную оценку 7. проводим определение параметров полученного уравнения и находим новые значения оценок 8. повторно вычисляем остатки и фактически возвращаемся к этапу 3.
42. Метод Хилдрета-Лу, используемый для оценки коэффициента автокорреляции случайного члена уравнения регрессии и коэффициентов самого уравнения регрессии, заключается в следующем:
1) В данном методе используется итерационная процедура. Находятся оценки факториальных переменных уравнения, далее вычисляются остатки, находится оценка коэффициента автокорреляции 2) В данном методе исследователь задает интервал изменения величины
3) В данном методе исследователь исключает один из факторов уравнения регрессии, который, по мнению исследователей, считается менее значимым, или имеет менее высокий коэффициент корреляции с результирующим фактором, или имеет более высокий коэффициент корреляции с другими факторами.
Какие системы алгебраических уравнений называются системами одновременных уравнений? 1) Уравнения, в которых одни переменные являются только объясняющими для всех уравнений, а другие переменные являются только результирующими переменными для всех уравнений. 2) Уравнения, в которых все переменные являются либо только объясняющими переменными, либо только результирующими переменными. 3) Уравнения, в которых одни и те же переменные в различных уравнениях используются как объясняющие переменные, так и результирующие переменные.
Почему нельзя определить параметры уравнения функции потребления простой кейнсианской модели формирования доходов? Т.к. результирующий признак коррелирует со случайной составляющей. Это приводит к смещению оценок уравнения регрессии. 2) Т.к. все переменные простой кейнсианской модели формирования доходов являются экзогенными переменными. 3) Т.к. первые два слагаемых правой части уравнения показывают, что совокупный уровень доходов зависит от постоянной составляющей (объема потребления и объема инвестиций)
Какие переменные считаются эндогенными переменными? Переменные, которые определяются внутри модели. 2) Переменные, которые задаются извне или берутся как заданные. 3) Переменные, которые коррелируют с внешними признаками.
Какие переменные считаются экзогенными переменными
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.94 (0.008 с.) |


 из авторегрессионной схемы I порядка, далее, используя данную оценку
из авторегрессионной схемы I порядка, далее, используя данную оценку 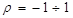 и шаг. Для каждого значения
и шаг. Для каждого значения 


