Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чему равен коэффициент эластичности для линейного алгебраического уравнения?Содержание книги
Поиск на нашем сайте
1. Что понимается под значимостью выборочных статистических показателей? - вероятность принятия нулевой гипотезы -степень совпадения Уфак. И Утеор. -соответствие показателя наиболее значимым свойствам или явлениям Как производится проверка значимости уравнения регрессии в целом? - c помощью F-критерия Фишера - с помощью t-критерия Стьюдента - с помощью ранговой корреляции Спирмена
43. Как формулируется «нулевая гипотеза» при определении статистической значимости уравнения регрессии в целом? 1) Каждый коэффициент уравнения регрессии в генеральной совокупности равен нулю. 2) Коэффициенты парной корреляции в генеральной совокупности равны нулю. 3) Коэффициенты уравнения регрессии в генеральной совокупности равны нулю, а0 = По какой формуле рассчитывается F- критерий Фишера? 1) F = σ2 y + σ2 ε 2) F = 3) F = Как формулируется «нулевая гипотеза» при определении статистической значимости отдельных коэффициентов уравнения регрессии? 1) Коэффициенты парной корреляции в генеральной совокупности равны нулю. Каждый коэффициент уравнения регрессии в генеральной совокупности равен нулю. 3) Коэффициенты уравнения регрессии в генеральной совокупности равны нулю, а0 = По какой формуле рассчитывается t- критерий Стьюдента 1) 2) t p = rx|ε| ×
47. Каким условиям должна отвечать остаточная компонента в уравнении регрессии для того, чтобы данное уравнение адекватно отражало изучаемые взаимосвязи между показателями: 1) случайность колебаний уровней остаточной последовательности; 2) математическое ожидание случайной компоненты не равно 0; 3) соответствие распределения случайной компоненты нормальному закону распределения; 4) значения уровней случайной компоненты независимы;
48. По какой формуле определяется доверительный интервал для отдельных коэффициентов уравнения регрессии: 1) аj - saj tкр £ aj £ aj + saj*tкр; 2) аj - saj tкр ³ aj ³ aj + saj*tкр; 3) аj + saj tкр £ aj £ aj + saj*tкр; 4) аj - saj tкр ³ aj ³ aj - saj*tкр ;
49. Какие коэффициенты характеризуют силу влияния на результирующий признак отдельных факторов и их совокупное влияние: 1) коэффициент парной корреляции; 2) коэффициент множественной корреляции;
3) коэффициент частной корреляции; 4) коэффициент множественной детерминации; Д) все ответы верны 50. Почему не имеет смысла путем повышения порядка уравнения регрессии добиваться равенства 0 остаточной случайной компоненты: 1) т.к. при повышении порядка уравнения регрессии, значение остаточной случайной компоненты будет увеличиваться; 2) не измениться; 3) т.к. нельзя добиться того чтобы остаточная случайная компонента была = 0; 4) все ответы не верны;
ВОПРОСЫ ДЛЯ ТЕСТОВ Глава 4, пункт 4.1.
1) выбор типа регрессии Определение формы связи функционального и факториального показателя 3) выбор функции, которая наилучшим образом аппроксимирует исходный статистический материал
1)себестоимость 2)фондоотдача 3)производительность труда
Прибыль / себестоимость продукции 2) прибыль / объём выпущенной продукции 3) выручка / себестоимость продукции
1) фондоотдача, рентабельность, инвестиции Производительность труда, себестоимость, фондоотдача 3) амортизационные отчисления, производительность труда, себестоимость
1) это отношение среднегодовой стоимости основных фондов к объёму выпущенной продукции 2) это показатель, характеризующий загрузку оборудования на производительности труда Это выработка продукции на один рубль основных производственных фондов
1) в расчёте многофакторной корреляционной линейной модели на ЭВМ В экономической постановке рассматриваемых задач и последующем переводе их описания с естественно-экономического языка на язык формально-экономический путем построения экономико-математических моделей, адекватных основному содержанию экономического процесса 3) в анализе хозяйственной деятельности предприятий с помощью таких показателей, как производительность труда, фондоотдача, себестоимость и рентабельность
Выбор результативного признака; отбор факториальных показателей; выбор и обоснование типа поверхности регрессии; сбор и первичная обработка данных; решение полученной модели на ЭВМ; экономико-математический анализ результатов решений 2) Выбор результативного признака; отбор факториальных показателей; расчёт коэффициентов парной корреляции; нахождение уравнения регрессии; выдвижение и проверка нулевых гипотез; оформление и сдача отчёта 3) Выбор результативного признака; отбор факториальных показателей; выбор и обоснование типа поверхности регрессии; решение полученной модели на ЭВМ; анализ результатов решений; оформление и сдача отчёта
1) показатель, находящийся в корреляционной связи с выбранным функциональным показателем 2) показатель, определяющий связь функционального и факториального показателей
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.238.81 (0.007 с.) |

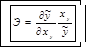 2.
2.  3.
3. 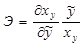

 .
.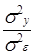

 3) t ф =
3) t ф =