
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значение коэффициента парной корреляции равное 0,8Содержание книги
Поиск на нашем сайте
5.Как можно устранить мультиколлениарность между факториальными признаками уравнения регрессии? 1) исключить факториальный признак вызывающий мультиколлениарность; 2) ее устранить нельзя; 3) провести дополнительные исследования;
6.Гетероскедастичность – это …. 1) явление, когда с изменением факториального признака (Х) демперсия случайной компоненты будет увеличиваться или уменьшаться, или изменяться по какому – либо другому закону; 2) это одинаковый разброс случайной компоненты; 3) это зависимость последующего значения от предыдущего;
7.Что понимается под дисперсией случайного члена уравнения регрессии ? 1) это возможное поведение случайного члена до того, как сделана выборка; 2) Показывает долю изменения Y, который можно объяснить изменением включенных в модель факторов; 3) характеризует тесноту связи функции Y с аргументами Xi, при условии, что прочие не включенные в уравнение регрессии аргументы этой функцией действуют корриляционно независимо от аргумента Xi; 8.Какой вид распределений случайнойго члена уравнения регрессии характерен для гомоскедастичного случая? 1) нормальное распределение кривой; 2) гипербола; 3)парабола;
9. Гетероскедастичность случайного члена уравнения регрессии приводит: 1) с изменением факториального признака (Х) дисперсия случайной компоненты будет увеличиваться или уменьшаться, или измениться по какому – либо закону; 2) с изменением факториального признака (Х) дисперсия случайной компоненты будет возрастать; 3) с изменением факториального признака (Х) дисперсия случайной компоненты будет уменьшаться;
10. Возможный способ снижения влияния гетероскедастичность случайного члена уравнения регрессии на оценки параметров уравнения регрессии: 1) придать наблюдению с малой дисперсией больший вес, а наблюдениям с большой дисперсией меньший вес; 2) придать наблюдению с малой дисперсией меньший вес, а наблюдениям с большой дисперсией больший вес; 3) невозможно снизить влияние гетероскедастичности случайного члена уравнения регрессии на оценки параметров уравнения регрессии;
11. При выполнении теста ранговой корреляции Спирмена предполагается: 1) дисперсия случайной составляющей будет либо увеличиваться, либо уменьшаться по мере увеличения Х; 2) дисперсия случайной составляющей будет неизменной по мере увеличения Х; 3) дисперсия случайной составляющей будет либо увеличиваться, либо уменьшаться при неизменной Х;
12. Для расчета коэффициента ранговой корреляции Спирмена необходимо упорядочить: 1) данные по Х и абсолютную величину e упорядочивают по возрастанию; 2) абсолютную величину e упорядочивают по возрастанию; 3) данные по Х и абсолютную величину e упорядочивают по убыванию;
13. Расчет коэффициента ранговой корреляции Спирмена производится по формуле:
   1. 1.
3.
14. Тестовая статистика в тесте ранговой корреляции Спирмена определяется по формуле: 1.
3. 15. Согласно тесту ранговой корреляции Спирмена нулевая гипотеза об отсутствии гетероскедастичности случайного члена уравнения регрессии будет отклонена при уровне значимости в 5 % если тестовая статистика… 1. tр < 1,96; 2. tр > 1,96; 3. tр = 1,96. 16. При проведении теста Голдфелда—Квандта предполагается… 1. Что стандартное отклонение σεi распределения вероятности εi обратнопропорционально значению x в этом наблюдении; 2. Что стандартное отклонение σεi распределения вероятности εi пропорционально значению x в этом наблюдении; 3. Случайная составляющая подвержена автокорреляции.
17. Для выполнения теста Голдфелда-Квандта имеющиеся наблюдения: Упорядочиваются по возрастанию Х 2) упорядочиваются по убыванию Х 3) все ответы верны.
18. В тесте Голдфелда-Квандта Нулевая гипотеза об отсутствии гетероскедостичности будет отклонена, если: 1) Fp>Fт 2) Fp<Fт 3) Fp=Fт
19. В тесте Голдфелда-Квандта рекомендуемое деление исходной выборки из 30 наблюдений на подвыборки составляет: Части 2) 2 части 3) 6частей
20. При проведении теста Глейзера предполагается: 1) что стандартное отклонение di связано с изменением факториального признака соотношением di=a’+b’*Xig 2) что распределение случайной компоненты соответствует нормальному закону распределения. 3) что случайная составляющая не подвержена автокорреляции.
21. Для нахождения регрессионной зависимости, характеризующей изменение гетероскедастичности случайного члена уравнения регрессии в тесте Глейзера, используется регрессионное уравнение вида: 1. 2. 3.
22. В тесте Глейзера нулевая гипотеза об отсутствии гетероскедастичности случайного члена уравнения регрессии будет отклонена, если в уравнении 1. величина 2. величина 3. величина 23. Для снижения влияния на оценки уравнения регрессии гетероскедастичности необходимо: 1. умножить коэффициенты уравнения регрессии на параметр, вызывающий гетероскедастичность; 2. вычесть из коэффициентов уравнения регрессии параметр, вызывающий гетероскедастичность;
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.181 (0.005 с.) |

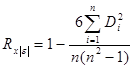





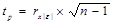

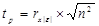
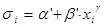 ;
; ;
;
 .
. будет значимо отличаться от 0;
будет значимо отличаться от 0; будет значимо отличаться от 0;
будет значимо отличаться от 0;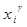 будет значимо отличаться от 0.
будет значимо отличаться от 0.


