Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какой недостаток имеет показатель точности модели – среднее квадратическое отклонение.Содержание книги
Поиск на нашем сайте
1) Он не зависит от масштаба y, а следовательно и различные σ мы можем получить только от одинаковых объектов 2) Он зависит от масштаба y, но для разных объектов мы не можем получить разные σ 3) Он зависит от масштаба y, т.е. для разных объектов мы можем получить разные σ
1) Показывает долю изменения y, объясняемую изменением включенных в модель факторов Показывает, какая доля в изменении результирующего признака может быть объяснена изменением не включенных в модель факторов 3) Показывает долю изменения y, объясняемая изменением не включенных в модель факторов
30. Что показывает коэффициент множественной детерминации R2? Показывает долю изменения y, объясняемую изменением включенных в модель факторов 2) Показывает, какая доля в изменении результирующего признака может быть объяснена изменением не включенных в модель факторов 3) Показывает долю изменения y, объясняемая изменением не включенных в модель факторов
С использованием какой формулы определяется величина коэффициента множественной детерминации? 1) 2)
3) Почему в большем числе случаев используется уравнение регрессии выраженное в виде линейного алгебраического уравнения? 1) потому что все экономические процессы описываются линейными алгебраическими уравнениями регрессии; 2) чтобы избежать смещенности оценок; в) потому что необходимо использовать линейный регрессионный анализ, который может быть применен только к линейным уравнениям.
33. Закон сложения дисперсий для функции: 1) общая дисперсия равна сумме дисперсии теоретических значений результирующего показателя и дисперсии фактических значений результирующего показателя; 2) общая дисперсия равна сумме дисперсии теоретических значений результирующего показателя и дисперсии остатков; в) общая дисперсия, равна сумме дисперсий, которые появляются под влиянием факториальных признаков включенных в модель.
Какая формула отображает остаточную дисперсию? а) б) в)
Что характеризует коэффициент множественной корреляции? 1) Коэффициент множественной корреляции характеризует влияние различных факторов на результирующий признак и взаимосвязи факторов между собой. Коэффициент множественной корреляции характеризует тесноту и линейность статистической связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат. 3) Коэффициент множественной корреляции характеризует долю изменения результирующего признака, которую можно объяснить изменением включенных в модель факторов.
С использованием какой формулы можно вычислить коэффициент парной корреляции? 1)
Что показывает коэффициент парной корреляции? 1) Коэффициент парной корреляции показывает тесноту связи функции y с аргументом xi и взаимосвязи аргументов между собой, при условии, что прочие, не включенные в уравнение регрессии аргументы этой функции действуют корреляционно независимо от аргумента xi. 2) Коэффициент парной корреляции характеризует долю изменения результирующего признака, которую можно объяснить изменением невключенных в модель факторов. 3) Коэффициент парной корреляции характеризует тесноту связи между результатом и соответствующим фактором.
Что показывает коэффициент частной корреляции? Коэффициент частной корреляции наилучшим образом характеризует силу индивидуального влияния каждого фактора, включенного в уравнение регрессии, на результирующий признак. 2) Коэффициент частной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат. 3) Коэффициент частной корреляции показывает, что два или более факторов связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга.
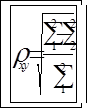
39. Величина коэффициента частной корреляции определяется по формуле: 1.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

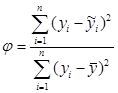 29.Что показывает коэффициент сходимости?
29.Что показывает коэффициент сходимости?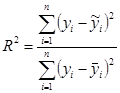 ;
;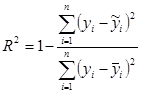 ;
;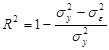 .
.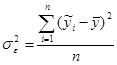 ;
;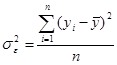 ;
;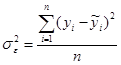 .
.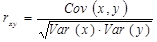 2)
2) 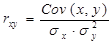 3)
3) 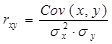
 2.
2. 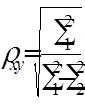 3.
3.