
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы Бернулли, Пуассона и Муавра-ЛапласаСодержание книги
Поиск на нашем сайте
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А. Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0<p<1), событие наступит ровно r раз (безразлично, в какой последовательности), равна
где q=1-p. Вероятность того, что событие наступит: а) менее r раз; б) более r раз; в) не менее r раз; г) не более r раз – находят соответственно по формулам: а) Pn( 0 )+Pn( 1 )+…+Pn(r- 1 ); б) Pn(r+ 1 )+Pn(r+ 2 )+…+Pn(n); в) Pn(r)+Pn(r+ 1 )+…+Pn(n); г) Pn( 0 )+Pn( 1 )+…+Pn(r). Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то пользуются приближенной формулой
где k – число появления события в n независимых испытаниях, l=np (среднее число появления события в n испытаниях) и говорят, что случайная величина распределена по закону Пуассона. Пример 29. Вероятность рождения мальчика 0.515. В семье 6 детей. Найти вероятность того, что из них: а) ровно три девочки, б) не более трех девочек, в) не менее двух, но не более четырех девочек. Решение: а)
б)
Пример 30. «Средний» человек с вероятностью 3/5 выполняет определенное задание за 1 мин. Предположим, что задание выполнялось 10 людьми. Какова вероятность ровно семи успешных выполнений задания за 1 мин? Решение. Здесь n = 10, k = 7, р = 3/5. Значит,
Пример 31. Предположим, что скрещиваются мышь-альбинос и мышь гомозиготного нормального типа (цветная). Какова вероятность двух альбиносов из шести мышей во втором поколении? Решение. В первом поколении все мыши будут цветными, так как ген альбинизма рецессивен. Легко видеть, что во втором поколении цветными окажутся 3/4 всех мышей. Поскольку все первое поколение имеет тип Сс, скрещивание Сс и Сс с равными вероятностями дает СС, Сс, сС и сс, причем лишь потомство сс является альбиносами. Таким образом, Р (альбинос) = 1/4 и задача сводится к распределению Бернулли при n = 6, k = 2 и р = 1/4. Искомая вероятность есть
Непосредственное применение формулы Бернулли при большом числе испытаний связано с громоздкими вычислениями, поэтому при больших n используют приближённую формулу Пуассона Рn (m)= Эту формулу применяют в случае, когда n несколько десятков и более, а произведение np <10 в случае, когда n велико, а np Если число испытаний n достаточно велико (n Рn (m)=
В условиях локальной формулы Муавра-Лапласа вероятность того, что число успехов лежит между m 1 и m 2 можно приближенно найти по интегральной формуле Муавра-Лапласа Рn (m 1 Функцию Ф(x) называют функцией Лапласа или интегралом вероятности. Значение интеграла для различных Поэтому вычисление вероятности сводится к расчету Завод отправил в магазин 5000 ампул с лекарством. Вероятность того, что в пути ампула разобьется, равно 0,0004. Найти вероятность того, что в пути повредится: а) равно 3 ампулы; б) не более 2 ампул. Решение: а) Рассматривая транспортировка каждой ампулы как отдельное испытание, можем утверждать, что производится n=5000 повторных испытаний. Пусть событие А – повреждение ампулы в пути. Так как вероятности наступления события А в каждом испытании одинаковы(p=0,0004),то эти испытания независимы. А значит, для вычисления вероятности повреждения в пути равно 3 ампул можно использовать формулу Бернулли:
Расчет вероятности по этой формуле достаточно сложен, поэтому воспользуемся приближенной формулой Пуассона. Так как p =0,0004< 0,1 и npq =5000 ·0,0004·0,9994≈2<10, поэтому:
где λ=n·p=5000·0,0004=2 – среднее число появления события А в 5000 испытаний.
б) Событие (m Следовательно, P(m Пример 33. Средняя плотность болезнетворных микробов в одном м3 воздуха равна 10. Берем на пробу 2 дм3 воздуха. Найти вероятность того, что в них будет обнаружен хотя бы один болезнетворный микроб. Решение: 1 дм3 = 0,001 м3. 2 дм3 = 0,002 м3. Вероятность присутствия 1 микроба в 2 дм3:
Количество испытаний: 10 Среднее число появлений событий А (1 микроба) в 10 испытаниях: Используем формулу Пуассона
Некоторое редкое заболевание встречается у 0.1% населения. Какова вероятность того, что это заболевание окажется у 4 человек из случайно отобранных 5000 человек? Решение: Вероятность заболевания р=0.001. n=5000. По формуле Пуассона
По статистическим данным в среднем 87% новорожденных доживают до 50 лет. Найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет: а) заключена в пределах от 0,9 до 0,95; б) будет отличаться от вероятности этого события не более,чем на 0,04 (по абсолютной величине). Решение: а) вероятность того, что новорожденный доживет до 50 лет, равна 0,87. Т.к. n = 1000 велико (условие npq =1000*0,87*0,13=113,1≥20 выполнено), то используем следствие интегральной теоремы Лапласа. Вначале определим по
Теперь по формуле
б) По формуле
Т. к. неравенство
Всхожесть семян оценивается вероятностью 0,8. Найти вероятность того, что из 100 высеянных семян взойдет: а) равно 90; б) от76 до 90 семян. Решение: а) Пусть событие А – семя взошло. Рассматривая посев каждого семени как отдельное испытание, можно сказать, что проводится 100 независимых испытаний (в каждом из них событие А наступает с постоянной вероятностью p = p(A) = 0,8). По формуле Бернулли имеем:
Понятно, что непосредственный расчет по этой формуле окажется трудным. В данной задаче произведение npq равно:
поэтому можно воспользоваться приближенной локальной формулой Лапласа:
По таблице значений функции Тогда
б) Обозначим как (76
Однако, т.к. np =16>10, то хорошую точность расчета искомой вероятности можно получить при использовании приближенной интегральной формулы Лапласа:
т.к. функция Лапласа нечетная и Ф (–1)= –Ф (1). По таблице значений Ф( Тогда Найдите наиболее вероятное число выигрышей в шахматы в 15 партиях у равносильного противника. Замечание. Для нахождения наиболее вероятного числа успехов k0 по заданным n и p можно воспользоваться неравенствами np-q<=k0<=np+p или правилом: если число np+p не целое, то k0 равно целой части этого числа; если же np+p целое, то k0 имеет 2 значения k0'=np-q и k0''=np+p. Решение. В этом примере n= 15, p= 0,5. Число np+p =15*0,5+0,5=7,5+0,5=8. Ответ: 8 раз.
Варианты заданий
№12.1. Вероятность успеха в эксперименте составляет 95%, а неудачи—-5%. Эксперимент повторяют пять раз. Определите вероятности следующих событий а) ни одного успеха: б) ни одной неудачи; в) четыре успеха и одна неудача. №12.2. В любой данный день в июне погода может быть хорошей (с вероятностью 50%), посредственной (с вероятностью 25%) или плохой (с вероятностью 25%). Предположим, что погода в данный день никак не влияет на погоду в любой другой день. Какова вероятность того, что в течение одной недели в июне будет семь хороших дней? четыре хороших дня, два посредственных и один плохой день? №12.3. В некоторой большой популяций у 40% людей волосы черные, у 40% рыжие и у 20% светлые. Если из популяции случайно выбирают 10 человек, то каковы вероятности следующих событий: а) 5 черноволосых, 5 рыжих; б) 4 черноволосых, 4 рыжих, 2 светловолосых; в) 3 черноволосых, 3 рыжих, 4 светловолосых? №12.4. Дальтонизмом страдает 1% большой популяции. Допустим, что из нее наугад выбирают n человек. Какова вероятность того, что ни один из n человек не окажется дальтоником? Сколь велико должно быть n, чтобы эта вероятность была меньше 10%? №12.5. Машина дает продукцию, которая должна удовлетворять определенным требованиям. Вероятность того, что данная единица продукции приемлема, составляет 95%. Из продукции машины делают выборку в количестве 10 ед. Какова вероятность того, что все 10 ед. продукции окажутся приемлемыми? №12.6. По оценкам, волк, в одиночку нападающий на лося, добивается успеха в 8% столкновений. Какова вероятность того, что в пяти столкновениях ни один лось не станет добычей волка? №12.7. В каждом полушарии человеческого мозга имеется четко определяемая слуховая область. В анатомических исследованиях было установлено, что слуховая область левого полушария более развита в 65% рассмотренных случаев, менее развита в 10% и развита в одинаковой с правым полушарием степени в 25% случаев. Какова вероятность того, что из группы в пять случайно выбранных человек в три эти категории соответственно попадут три, ни одного и два человека? №12.8. Замечено, что слушатели вводного курса по количественному химическому анализу достигают приемлемых результатов в 80% титрований. Один студент добился приемлемого результата лишь однажды в шести титрованиях. Какова вероятность случайного наступления этого события? Как вы думаете, станет ли этот студент химиком-экспериментатором? №12.9. При заболеваниях щитовидной железы применяется йодная терапия. Было замечено, что у 50% больных наступает быстрое улучшение, на 40% больных терапия не оказывает заметного эффекта, а у 10% она вызывала ухудшение состояния. Эту терапию применяют девять больных. Каковы вероятности того, что: а) все девять почувствуют улучшение; б) у пятерых будет улучшение, трое останутся в прежнем состоянии и одному станет хуже; в) у троих будет, улучшение, трое останутся в прежнем состоянии и троим станет хуже? №12.10. Лечение одного заболевания приводит к выздоровлению в 75% случаев. Лечилось шесть больных. Каковы вероятности того, что: а) выздоровят все шестеро; б) не выздоровит ни один; в) выздоровят по крайней мере четверо? №12.11. Шесть человек больны заболеванием, для которого коэффициент выздоровления составляет 98%. Каковы вероятности того, что: а) выздоровят все шестеро; б) ни один не выздоровит; б) выздоровят только пятеро? №12.12. Шансы волка добыть пищу за каждый период охоты составляют 60%. Какова вероятность того, что успешными оказалось больше половины всех периодов охоты, если всего был 31 период? если всего было 14 периодов? №12.13. а) Сколько нужно бросить костей, чтобы вероятность выпадения нечетного числа хотя бы на одной из них была больше 90%? б) Сколько нужно бросить костей, чтобы вероятность выпадения хотя бы одной пятерки была больше 50%? №12.14. В одном городе 50% населения предпочли бы более строгий контроль за огнестрельным оружием, 30% — более слабый контроль и 20% хотели бы сохранить существующее положение вещей. Для опроса выбрано случайным образом 12 человек. Каковы вероятности того, что: а) все хотят усилить контроль; б) половина опрошенных хотят усилить, а половина — ослабить контроль; в) равные количества опрошенных предпочитают три альтернативы? №12.15. Метеоролог обращается за субсидией для поездки в Испанию с целью проверки теории о том, что «дождь в Испании идет в основном на равнине». Он планирует провести наблюдения в такое время года, когда вероятность дождя на равнине в любой данный день составляет 20%. (Предполагается, что эта, вероятность не зависит от предшествующей погоды.) а) Сколько дней должен запланировать метеоролог провести в Испании, чтобы на 99% быть уверенным в том, что он застанет дождь? б) Допустим, что метеорологу были выделены денежные средства на 15 дней в Испании и что за первые 10 дней не было ни одного дождя. Какова вероятность того, что его поездка окажется неудачной, т. е. что он не увидит ни одного дождя? №12.16. В популяции дрозофилы у 20% особей имеется мутация крыльев. Если из популяции выбирают наугад шесть мух, то какова вероятность мутации у двух из них? по крайней мере у одной? меньше чем у пяти? №12.17. Кофеин и бензедрин считаются стимуляторами, имеющими некоторую способность противодействовать угнетающему влиянию алкоголя. В эксперименте по проверке их относительной эффективности 40 добровольцев приняли по 6 унций алкоголя каждый. Добровольцы были разбиты затем на 20 пар, и один член каждой пары получал бензедрин, а другой — кофеин. Согласно некоторому тесту, бензедрин приводил к более быстрому восстановлению во всех 20 парах. Какова вероятность такого результата, если считать, что в воздействии кофеина и бензедрина нет никакой разницы? №12.18. В хлопке имеется 10% коротких волокон. Какова вероятность того, что в наудачу взятом пучке из пяти волокон окажется не более двух коротких? №12.19. Всхожесть семян данного растения оценивается вероятностью 0,8. Найти вероятность того, что из 8 посеянных семян взойдёт не менее 6. №12.20. Найти наивероятнейшее число появлений некоторого события при 16 испытаниях, если вероятность появления его в отдельном испытании равна 0,7. №12.21. Число длинных волокон в партии хлопка составляет в среднем 0,6 общего количества волокон. При каком общем количестве волокон хлопка наивероятнейшее число длинных окажется равным 20? №12.22. На каждые 20 приборов приходится в среднем 6 неточных. Определить наивероятнейшее число точных приборов из наудачу взятых 8 приборов. №12.23. Если в среднем левши составляют 1 %, то какова вероятность того, что среди 200 человек: 1) 4 левши; 2) по крайней мере 4 левши. №12.24. В аптеку поступило 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Определить вероятность того, что аптека получит разбитых бутылок: 1) ровно одну; 2) хотя бы одну. №12.25. Дежурная аптека обслуживает 20000 населения. Вероятность того, что в ночное время один посетитель придет в аптеку, равна 0,0002. Найти вероятность того, что в ночное время в аптеку: а) никто не придет; б) придут 3 посетителя; в) придет хотя бы один посетитель. Случайные величины Случайная величина - это величина, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно - заранее неизвестно). Дискретная случайная величина - это случайная величина, когда принимает отдельное изолированное, счетное множество значений. Непрерывная случайная величина - это случайная величина, принимающая любые значения из некоторого интервала. Понятие непрерывной случайной величины возникает при измерениях. Случайные величины обозначаются конечными заглавными буквами латинского алфавита X, Y, Z, а их значения - соответствующими строчными буквами х, у, z.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.71.166 (0.008 с.) |


 ,
,





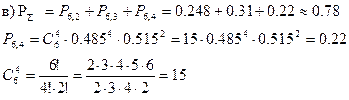


 , где
, где 
 10, то формула Пуассона даёт очень грубое приближение, и для расчётов вероятности используют формулу Муавра-Лапласа.
10, то формула Пуассона даёт очень грубое приближение, и для расчётов вероятности используют формулу Муавра-Лапласа. 100),произведение npq
100),произведение npq  х), где х =
х), где х =  ,
,  (х)=
(х)=  – функция Гаусса
– функция Гаусса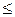 m
m  , х 2=
, х 2=  , Ф 0(х)=
, Ф 0(х)=  – функция Лапласа, Ф 0(х) – нечетная.
– функция Лапласа, Ф 0(х) – нечетная. вычислены и приведены в таблицах, причем только для
вычислены и приведены в таблицах, причем только для  . Для нахождения Ф(x) функции для отрицательных значений
. Для нахождения Ф(x) функции для отрицательных значений  пользуются той же таблицей, учитывая, что Ф(x) - нечетная функция, т.е.
пользуются той же таблицей, учитывая, что Ф(x) - нечетная функция, т.е.  Кроме того, в таблице приведены значения лишь до
Кроме того, в таблице приведены значения лишь до  можно принять
можно принять 
 и дальнейшему определению по таблице
и дальнейшему определению по таблице 

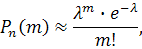
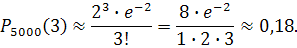
 2) является суммой трех несовместимых событий (m =0), (m =1) и (m =2).
2) является суммой трех несовместимых событий (m =0), (m =1) и (m =2). (1+2+2)
(1+2+2)  0,135·5≈0,677
0,135·5≈0,677






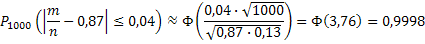
 равносильно неравенству
равносильно неравенству  , что от 0,83 до 0,91 новорожденных из 1000 доживут до 50 лет.
, что от 0,83 до 0,91 новорожденных из 1000 доживут до 50 лет.


 найдем:
найдем: 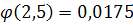 .
.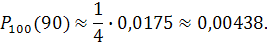
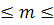 90) событие, заключающееся в том, что число m взошедших семян заключено между 76 и 90. Если для вычисления вероятности этого события использовать формулу Бернулли, то придется считать следующую сумму вероятностей:
90) событие, заключающееся в том, что число m взошедших семян заключено между 76 и 90. Если для вычисления вероятности этого события использовать формулу Бернулли, то придется считать следующую сумму вероятностей:





