
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки параметров распределения. Выборочные характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Характеристики положения
Мода ( Для одномодальных распределений мода – это наиболее часто встречающаяся варианта в данной совокупности. Например, для распределения:
Для определения моды интервальных рядов служит формула:
где
Определить моду ряда распределения кальция (мг %) в сыворотке крови обезьян.
Решение: Частота модального класса
Найдите моду распределения роста 1000 взрослых мужчин:
Решение:
Медиана Ме – это значение признака, относительно которого ряд распределения делится на 2 равные по объему части. Например, в распределении: 12 14 16 18 20 22 24 26 28 медианой будет центральная варианта, т.е. Ме = 20, так как по обе стороны от нее отстоит по 4 варианты. Для ряда с четным числом членов 6 8 10 12 14 16 18 20 22 24 медианой будет полусумма его центральных членов, т.е.
Выборочная средняя – это среднее арифметическое значение вариант статистического ряда
В выборке взрослых мужчин n = 50 определяли содержание гемоглобина в крови. У Решение: По формуле:
13.2.2. Характеристики рассеяния вариант вокруг своего среднего Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения:
Среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии:
Коэффициент вариации СV – это отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах:
Коэффициент вариации – это мера относительной изменчивости случайной величины, которая позволяет сравнивать разнородные величины, например, частоту сердечных сокращений (ЧСС, уд/мин), артериальное давление (АД, мм. рт. ст.) и температуру (
Пример 4. Выборочная совокупность задана таблицей распределения:
Найти выборочную дисперсию. Решение: Найдем выборочную среднюю:
Найдем выборочную дисперсию:
Сравните 2 варьирующихся признака. Один характеризуется средней Решение:
Ответ: первый, так как
Варианты заданий Найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение, если совокупность задана таблицей распределения: № 13.1.
№ 13.2.
№ 13.3.
№ 13.4.
№ 13.5.
№ 13.6.
Оценка параметров генеральной совокупности по ее выборке Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема n, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах в целом.
Числовые значения, характеризующие генеральную совокупность, называются параметрами. Одна из задач математической статистики - определение параметров большого массива по исследованию его части. Статистическое оценивание может выполняться двумя способами: 1) точечная оценка – оценка параметра, которая дается в виде одного числа (точки); 2) интервальная оценка – по данным выборки оценивается интервал, в котором лежит истинное значение с заданной вероятностью.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.245.158 (0.005 с.) |

 ) – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости или
) – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости или  , такое, что n(
, такое, что n(
 , так как
, так как  =20=max.
=20=max.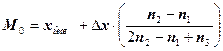
 - нижняя граница модального интервала, т. е. интервала с наибольшей частотой встречаемости
- нижняя граница модального интервала, т. е. интервала с наибольшей частотой встречаемости  ;
;  - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; 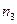 - частота интервала, следующего за модальным;
- частота интервала, следующего за модальным;  - ширина интервала.
- ширина интервала. . Частота класса, предшествующего модальному,
. Частота класса, предшествующего модальному, 



 есть оценка математического ожидания случайной величины по выборке.
есть оценка математического ожидания случайной величины по выборке.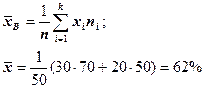
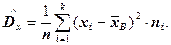 Исправленная дисперсия при малых выборках n<30
Исправленная дисперсия при малых выборках n<30 
 – исправленное значение (n<30).
– исправленное значение (n<30). 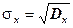

 ) в единых единицах - процентах.
) в единых единицах - процентах.

 = 2,4 кг и средним квадратическим отклонением
= 2,4 кг и средним квадратическим отклонением  = 0,58 кг, другой - величинами
= 0,58 кг, другой - величинами  = 8,3 см и
= 8,3 см и  = 1,57 см. Какой признак варьируется сильнее?
= 1,57 см. Какой признак варьируется сильнее?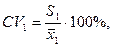

 .
.



