
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы для вычисления первой производнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Численное дифференцирование весьма чувствительно к погрешностям, вызванным неточностью исходных данных. Значительно меньшую погрешность имеет дифференцирование многочленов наилучшего среднеквадратического приближения (методом наименьших квадратов). На практике часто применяются формулы безразностного дифференцирования для производной первого порядка: По трем точкам:
По четырем точкам:
По пяти точкам:
Формулы второй производной
По четырем точкам:
По пяти точкам:
Заметим, что с ростом порядка производной резко падает точность численного дифференцирования. Поэтому на практике редко применяют формулы для производных второго порядка.
Примеры
№1. Пользуясь безразностными формулами по 3 точкам, определить первые производные для функции у=х 2 на интервале [1; 3] с шагом 0,2 и сравнить их значения с аналитическими. Решение. Воспользуемся формулами (5.1):
Для сравнения этих значений с аналитическими составим таблицу:
Таким образом, мы видим, что все значения первой производной полностью совпадают с аналитическими. №2. Пользуясь безразностными формулами по 4 точкам, определить первые производные для функции у=х 3 на отрезке [1; 3] с шагом 0,2 и сравнить эти значения с аналитическими. Решение. Пользуемся формулами (5.2):
Для сравнения полученных значений с аналитическими составим таблицу:
Получим, что для функции у=х 3 численное дифференцирование по 4 точкам дает такие же значения, что и аналитические. №3. Найти вторую производную для функции у=х 3 на отрезке [1; 3] с шагом 0,2, пользуясь безразностными формулами по 4 точкам и сравнить полученные значения с аналитическими.
Решение. Воспользуемся формулами (5.4):
Для сравнения составим таблицу:
Таким образом, получим, что для функции у=х 3 численное нахождение второй производной по 4 точкам дает такие же значения, что и аналитические. Варианты заданий
№ 5.1. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 4 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими. 1. у=ех; 2. 3. у= ln x; 4. 5. y= sin x; 6. y=e 2 x; 7. 8. у= (х– 1 ) 2; 9. y= cos x; 10. y =ln x 2;
№ 5.2. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 3 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими. 11. у =sin x; 12. y =cos x; 13. y =sin (x 2 ); 14. y =sin2 x; 15. y =cos2 x; 16. y =sin ( 2 x); 17. y =cos ( 2 x); 18. 19. y= ln2 x; 20. y= ln3 x;
№ 5.3. Для перечисленных функций, пользуясь безразностными формулами по 4 точкам, найти вторые производные в точках от 1 до 3 с шагом 0,2 и сравнить полученные значения с аналитическими. 21. y = e 2 x ; 22. 23. 24. у =(х –1)2; 25. y =ln(x 2); 26. y = 27. y= sin2 x; 28. 29. 30.
5.5. Контрольные вопросы Глава 6 Основы интерполяции. Постановка задачи
Пусть некоторая функция f(x) задана таблично на интервале [a,b] f (xn)=yn, f(x1)=y1,..., f(xn)=yn (6.1) Под интерполяцией понимается нахождение по таблице значений функции её аналитического описания, позволяющего вычислять значение этой функции от аргумента отсутствующего в таблице, т.е. так называемое чтение "между" строк. Задача сводится к построению функции f(x) (интерполирующей функции), принадлежащей известному классу функций и принимающей в точках x0, x1, x2,..., xn (узлах интерполяции) те же значения, что и функция f(x0)=y0, f(x1)=y1,..., f(xn)=yn, а в остальных точках отрезка [a,b] приближённо представляющая функцию f(x) с какой-то степенью точности.
При этом допускают, что f(x) непрерывна на отрезке [a,b] и имеет на нём в каждой точке конечные производные любого порядка, а узлы интерполирования отличны друг от друга. Через точки x0, x1, x2 ,..., xn можно провести бесчисленное множество кривых (рис. 6.1). Следовательно, задача отыскания функции f(x) по её значениям, поставленная таким образом, является неопределённой: можно построить бесчисленное множество функций принимающих при x0, x1, x2 ,..., xn, значение y0, y1, y2,..., yn
Рис. 6.1
Чтобы получить единственную f(x) наложим на неё дополнительные ограничения, а именно, в качестве f(x) используем полином P(x) степени на единицу меньше числа заданных значений n +1.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.169.46 (0.013 с.) |


 (5.1)
(5.1)

 ; (5.2)
; (5.2) ;
; .
. ;
; ;
; ; (5.3)
; (5.3) ;
; .
.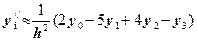 ; (первое значение)
; (первое значение) ; (внутренние точки) (5.4)
; (внутренние точки) (5.4) . (последнее значение)
. (последнее значение) ;
; ;
; ; (5.5)
; (5.5)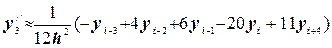 ;
; .
.













 и т.д. по формуле для
и т.д. по формуле для  .
. (первое значение)
(первое значение)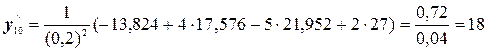 (последнее значение)
(последнее значение)
 и т.д. по формуле для внутренних точек.
и т.д. по формуле для внутренних точек. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.



