

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Раздел VI. Исследование функций с помощью производных
Похожие статьи вашей тематики
Как уже говорилось выше, основное применение производной  состоит в том, что она помогает исследованию самой функции состоит в том, что она помогает исследованию самой функции  , т.е. исследованию характера зависимости переменной , т.е. исследованию характера зависимости переменной  от переменной от переменной  , выраженного соотношением , выраженного соотношением  . Что же именно чаще всего интересует при исследовании характера зависимости одного фактора от другого? Приведем пример. Пусть имеется функциональная зависимость объема урожая . Что же именно чаще всего интересует при исследовании характера зависимости одного фактора от другого? Приведем пример. Пусть имеется функциональная зависимость объема урожая  (в тоннах, килограммах, граммах – у кого как) от количества (в тоннах, килограммах, граммах – у кого как) от количества  внесенных удобрений (в тех же единицах), выраженная формулой внесенных удобрений (в тех же единицах), выраженная формулой  . Допустим, мы внесли какое-то количество удобрений . Допустим, мы внесли какое-то количество удобрений  и ждем соответствующий урожай в количестве и ждем соответствующий урожай в количестве 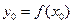 . Пусть появилась возможность дополнительно внести удобрения в количестве . Пусть появилась возможность дополнительно внести удобрения в количестве  единиц. Стоит ли это делать? Будет ли урожай больше или мы уже внесли столь много удобрений, что дальнейшее увеличение его количества только нанесет вред урожаю? Вопрос сводится к следующему: будет ли при увеличении аргумента единиц. Стоит ли это делать? Будет ли урожай больше или мы уже внесли столь много удобрений, что дальнейшее увеличение его количества только нанесет вред урожаю? Вопрос сводится к следующему: будет ли при увеличении аргумента  (с (с  до до  + +  ) увеличиваться и значение функции ) увеличиваться и значение функции  или же оно будет уменьшаться? Это зависит от самого значения или же оно будет уменьшаться? Это зависит от самого значения  , Точнее, принадлежит ли оно так называемому интервалу возрастания функции , Точнее, принадлежит ли оно так называемому интервалу возрастания функции  или интервалу ее убывания. Нахождению таких интервалов и поможет производная (дальше, в разделе «Монотонные функции»). Ну и конечно же нас должен интересовать вопрос о том, какое количество удобрений или интервалу ее убывания. Нахождению таких интервалов и поможет производная (дальше, в разделе «Монотонные функции»). Ну и конечно же нас должен интересовать вопрос о том, какое количество удобрений  является оптимальным (т.е. при таком количестве удобрений урожай максимален). Это сводится к нахождению такой точки (числа) является оптимальным (т.е. при таком количестве удобрений урожай максимален). Это сводится к нахождению такой точки (числа)  , чтобы значение функции , чтобы значение функции  в этой точке (т.е. число в этой точке (т.е. число 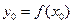 ) было бы больше, чем в остальных точках. Нахождению таких чисел тоже поможет производная (в разделе «Экстремумы функции»). ) было бы больше, чем в остальных точках. Нахождению таких чисел тоже поможет производная (в разделе «Экстремумы функции»).
Монотонные функции
Пусть нам задана некоторая функция  . Обратимся к ее геометрическому образу, каковым является график этой функции. Пусть эта функция имеет график, изображенный на рисунке. . Обратимся к ее геометрическому образу, каковым является график этой функции. Пусть эта функция имеет график, изображенный на рисунке.
Из графика видно, что над интервалом  оси оси  график идет вниз, а над интервалом график идет вниз, а над интервалом  вверх. Попробуем разобраться, как это сказывается на характере зависимости вверх. Попробуем разобраться, как это сказывается на характере зависимости  от от  . Возьмем произвольные две точки . Возьмем произвольные две точки  и и  из интервала из интервала  (так что (так что  > >  ) и с помощью графика определим значения ) и с помощью графика определим значения  и и  функции функции  в этих точках (см. рисунок). Поскольку кривая графика идет вниз, то число в этих точках (см. рисунок). Поскольку кривая графика идет вниз, то число  на оси на оси  будет ниже числа будет ниже числа  , а потому , а потому
 < <  . Итак, видно, что если график над некоторым интервалом оси . Итак, видно, что если график над некоторым интервалом оси  идет вниз, то большему значению идет вниз, то большему значению  из этого интервала соответствует меньшее значение функции (т.е. для любых чисел из этого интервала соответствует меньшее значение функции (т.е. для любых чисел  и и  из этого интервала: из этого интервала:  > >  => =>    ). Естественно назвать такой интервал интервалом убывания функции ). Естественно назвать такой интервал интервалом убывания функции  . Аналогично возьмем произвольные две точки . Аналогично возьмем произвольные две точки  и и  из интервала из интервала  (так что (так что  > >  ) и с помощью графика определим значения функции ) и с помощью графика определим значения функции  в этих точках (см. тот же рисунок). Поскольку кривая графика идет вверх, то значение в этих точках (см. тот же рисунок). Поскольку кривая графика идет вверх, то значение  на оси на оси  будет выше значения будет выше значения  , а потому , а потому
 > >  . Итак, видно, что если график над некоторым интервалом оси . Итак, видно, что если график над некоторым интервалом оси  идет вверх, то большему значению идет вверх, то большему значению  из этого интервала соответствует большее значение функции (т.е. для любых чисел из этого интервала соответствует большее значение функции (т.е. для любых чисел  и и  из этого интервала: из этого интервала:  . Естественно назвать такой интервал интервалом возрастания функции . Естественно назвать такой интервал интервалом возрастания функции  . Для сокращения записи вводятся следующие обозначения: . Для сокращения записи вводятся следующие обозначения:  – функция ) – функция )  убывает на интервале убывает на интервале  , ,  – функция – функция  возрастает на интервале возрастает на интервале  . Функция называется монотонной на некотором интервале . Функция называется монотонной на некотором интервале  , если она является возрастающей на всем этом интервале или убывающей на всем этом интервале. Понятно, что одна и та же функция на одних интервалах может возрастать, а на других убывать. Для приведенной выше функции интервалами монотонности будут интервалы , если она является возрастающей на всем этом интервале или убывающей на всем этом интервале. Понятно, что одна и та же функция на одних интервалах может возрастать, а на других убывать. Для приведенной выше функции интервалами монотонности будут интервалы  и и  . А, например, интервал . А, например, интервал  таковым не будет, так как на одной его части функция убывает, а на другой возрастает. Как же находить интервалы монотонности? Конечно, если имеется график функции, то эти интервалы просто видны. Но чаще всего графика нет, а есть только формула таковым не будет, так как на одной его части функция убывает, а на другой возрастает. Как же находить интервалы монотонности? Конечно, если имеется график функции, то эти интервалы просто видны. Но чаще всего графика нет, а есть только формула  ,выражающая зависимость ,выражающая зависимость  от от  . В этом случае опять помогает производная. Обратимся к рисункам. . В этом случае опять помогает производная. Обратимся к рисункам.
 
На левом рисунке изображен график возрастающей на соответствующем интервале функции, а на правом − убывающей. Попробуем почувствовать разницу. Берем произвольную точку  на интервале возрастания функции (левый рисунок) и проводим касательную к графику функции в соответствующей точке. Тогда в случае возрастания функции из рисунка видно, что касательная образует острый угол на интервале возрастания функции (левый рисунок) и проводим касательную к графику функции в соответствующей точке. Тогда в случае возрастания функции из рисунка видно, что касательная образует острый угол  с осью с осью  . По геометрическому смыслу производной . По геометрическому смыслу производной  . Поскольку тангенсы острых углов положительны, то . Поскольку тангенсы острых углов положительны, то  . Аналогично, берем произвольную точку . Аналогично, берем произвольную точку  на интервале убывания функции (правый рисунок) и проводим касательную к графику функции в соответствующей точке. Тогда в случае убывания функции из рисунка видно, что касательная образует тупой угол на интервале убывания функции (правый рисунок) и проводим касательную к графику функции в соответствующей точке. Тогда в случае убывания функции из рисунка видно, что касательная образует тупой угол  с осью с осью  (напомним, что угол меряется от оси (напомним, что угол меряется от оси  против часовой стрелки). По геометрическому смыслу производной снова против часовой стрелки). По геометрическому смыслу производной снова  . Поскольку тангенсы тупых углов отрицательны, то . Поскольку тангенсы тупых углов отрицательны, то  . Итак, мы наглядно убедились в том, что если функция возрастает на некотором интервале, то во всех точках этого интервала производная (если она существует) положительна (возможно, обращаясь в некоторых точках в 0), а во всех точках интервала убывания производная отрицательна. Справедлива соответствующая . Итак, мы наглядно убедились в том, что если функция возрастает на некотором интервале, то во всех точках этого интервала производная (если она существует) положительна (возможно, обращаясь в некоторых точках в 0), а во всех точках интервала убывания производная отрицательна. Справедлива соответствующая
Теорема. Пусть функция  дифференцируема на интервале дифференцируема на интервале  . Тогда . Тогда  (соответственно, (соответственно,  ) тогда и только тогда, когда ) тогда и только тогда, когда  (соответственно, (соответственно,  ) для всех значений ) для всех значений  из этого интервала. из этого интервала.
Отсюда следует, что для нахождения интервалов монотонности функции  не обязательно иметь перед глазами ее график. Достаточно найти ее производную и определить ее знаки. На тех интервалах, где производная положительна (точнее, неотрицательна), функция возрастает, а на интервалах отрицательности производной сама функция убывает. не обязательно иметь перед глазами ее график. Достаточно найти ее производную и определить ее знаки. На тех интервалах, где производная положительна (точнее, неотрицательна), функция возрастает, а на интервалах отрицательности производной сама функция убывает.
 Пример 1. Найти промежутки монотонности функции Пример 1. Найти промежутки монотонности функции  . .
Решение. Эта функция выбрана в качестве примера потому, что хорошо известен ее график (парабола, см. рисунок). Поэтому, даже не пользуясь приведенной теоремой, можно заранее сказать, что  и и  . Попробуем получить этот же результат с помощью приведенной теоремы, не обращаясь к графику. В нашем примере . Попробуем получить этот же результат с помощью приведенной теоремы, не обращаясь к графику. В нашем примере  , а потому , а потому  . Понятно, что выражение . Понятно, что выражение  для производной положительно для всех положительных х и отрицательно для всех отрицательных. Поэтому производная для производной положительно для всех положительных х и отрицательно для всех отрицательных. Поэтому производная  для отрицательных для отрицательных  и и  для положительных для положительных  . И делаем на основании теоремы тот же вывод об интервалах монотонности: . И делаем на основании теоремы тот же вывод об интервалах монотонности: 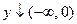 и и  . .
Экстремумы функции
Пусть нам задана некоторая функция  . Снова обратимся к ее геометрическому образу, каковым является ее график (см. рисунок). . Снова обратимся к ее геометрическому образу, каковым является ее график (см. рисунок).

Мы уже выяснили, что означает движение графика вниз и вверх над разными интервалами на оси  (интервалы монотонности). Теперь обратим внимание на самые высокие и самые низкие точки графика (точки А, B и С). Спроектируем эти точки на ось (интервалы монотонности). Теперь обратим внимание на самые высокие и самые низкие точки графика (точки А, B и С). Спроектируем эти точки на ось  , получим точки (числа) , получим точки (числа)  , ,  , и , и  . Чем числа-точки интересны? Найдем (по графику), например, значение функции в точке . Чем числа-точки интересны? Найдем (по графику), например, значение функции в точке  . Мы снова дойдем до самой высокой точки С и спроектируем ее на ось . Мы снова дойдем до самой высокой точки С и спроектируем ее на ось  . Получим значение . Получим значение  на оси на оси  . Если найдем теперь (тоже по графику) значения функции в близких к . Если найдем теперь (тоже по графику) значения функции в близких к  точках справа или слева, то их значения получатся уже меньше, чем точках справа или слева, то их значения получатся уже меньше, чем  . Поэтому точка . Поэтому точка  характерна тем, что значение функции в ней больше, чем значения функции в ближайших к ней точках. Естественно такую точку назвать точкой максимума функции характерна тем, что значение функции в ней больше, чем значения функции в ближайших к ней точках. Естественно такую точку назвать точкой максимума функции  . Точкой максимума является и точка . Точкой максимума является и точка  . А вот точка . А вот точка  характерна тем, что значение функции в ней меньше значений функции в ближайших к ней точках (именно ближайших, поскольку есть точки – подальше справа от характерна тем, что значение функции в ней меньше значений функции в ближайших к ней точках (именно ближайших, поскольку есть точки – подальше справа от  , в которых значения функции еще меньше). Такую точку естественно назвать точкой минимума функции , в которых значения функции еще меньше). Такую точку естественно назвать точкой минимума функции  . Итак, примем следующее определение. Точка (число) . Итак, примем следующее определение. Точка (число)  называется точкой максимума (соответственно, минимума) функции называется точкой максимума (соответственно, минимума) функции  , если значение функции в этой точке , если значение функции в этой точке  больше (соответственно, меньше) значений функции в ближайших к больше (соответственно, меньше) значений функции в ближайших к  точках (т.е. точках из некоторой окрестности точки точках (т.е. точках из некоторой окрестности точки  ). Точки максимума и минимума функции называются точками экстремума этой функции. У функции, график которой изображен выше, три точки экстремума: ). Точки максимума и минимума функции называются точками экстремума этой функции. У функции, график которой изображен выше, три точки экстремума:  , ,  , и , и  . Как же находить точки экстремума функции? Если . Как же находить точки экстремума функции? Если  имеется график функции, то снова проблем не возникает – достаточно спроектировать на ось имеется график функции, то снова проблем не возникает – достаточно спроектировать на ось  самые высокие и низкие точки графика. Если же графика нет (как это обычно и бывает), а есть только формула самые высокие и низкие точки графика. Если же графика нет (как это обычно и бывает), а есть только формула  ,выражающая зависимость ,выражающая зависимость  от от  , то здесь опять помогает производная. , то здесь опять помогает производная.
Снова обратимся к графику той же функции (см. рисунок). Мы уже знаем, что для выяснения роли производной надо строить касательные к графику и использовать геометрический смысл производной. Построим касательные к графику в интересующих нас точках А, B и С. Они отличаются от касательных в других точках графика тем, что оказываются параллельными оси  . Параллельные прямые образуют друг с другом нулевой угол. Поэтому, по геометрическому смыслу производной, ее (производной) значения в этих точках равны тангенсу нуля (который равен 0): . Параллельные прямые образуют друг с другом нулевой угол. Поэтому, по геометрическому смыслу производной, ее (производной) значения в этих точках равны тангенсу нуля (который равен 0):  , ,  , ,  . Итак, мы получили, что в точках экстремума производная обращается в 0 (если она, конечно, в этих точках вообще существует). Этот факт выражает следующая . Итак, мы получили, что в точках экстремума производная обращается в 0 (если она, конечно, в этих точках вообще существует). Этот факт выражает следующая
Теорема Ферма (необходимое условие экстремума). Пусть функция  задана на интервале задана на интервале  , содержащем точку , содержащем точку  , в которой существует производная , в которой существует производная  . Тогда если . Тогда если  является точкой экстремума, то является точкой экстремума, то  . .
Утверждение теоремы можно переформулировать так: если функция  имеет локальный экстремум в точке имеет локальный экстремум в точке  , то либо , то либо
1) производная в этой точке существует и равна нулю:  , ,
либо
2) производная в этой точке  не существует. не существует.
Точка  , удовлетворяющая хотя бы одному из этих условий, называется критической точкой функции , удовлетворяющая хотя бы одному из этих условий, называется критической точкой функции  . Точка . Точка  , удовлетворяющая первому условию (т.е.: , удовлетворяющая первому условию (т.е.:  ),называется стационарной точкой функции ),называется стационарной точкой функции  . В критической точке касательная либо параллельна оси . В критической точке касательная либо параллельна оси  (если это стационарная точка), либо ее (касательной) вовсе не существует. Таким образом, из теоремы Ферма следует, что экстремумы функции, заданной на интервале (если это стационарная точка), либо ее (касательной) вовсе не существует. Таким образом, из теоремы Ферма следует, что экстремумы функции, заданной на интервале  , могут находиться только среди ее критических точек на этом интервале. Скажем несколько слов о ситуации, когда производная функции , могут находиться только среди ее критических точек на этом интервале. Скажем несколько слов о ситуации, когда производная функции  в некоторой точке в некоторой точке  не существует. Если функция все же непрерывна в этой точке, то отсутствие производной означает, что график функции в соответствующей точке испытывает «излом», т.е. нет плавного перехода графика через эту точку. Рассмотрим в качестве иллюстрации следующий не существует. Если функция все же непрерывна в этой точке, то отсутствие производной означает, что график функции в соответствующей точке испытывает «излом», т.е. нет плавного перехода графика через эту точку. Рассмотрим в качестве иллюстрации следующий
Пример 1. Рассмотрим функцию  . Эта функция непрерывна на всей числовой прямой. Найдем выражение для производной этой функции: . Эта функция непрерывна на всей числовой прямой. Найдем выражение для производной этой функции:  . Стационарных точек у функции нет (числитель дроби не обращается в 0 ни при каких значениях . Стационарных точек у функции нет (числитель дроби не обращается в 0 ни при каких значениях  ), однако, в точке ), однако, в точке   производная не существует (делить на 0 нельзя). Поэтому производная не существует (делить на 0 нельзя). Поэтому  – единственная критическая точка функции (в ней производная не существует). Каково же поведение графика функции в окрестности такой точки? График функции – единственная критическая точка функции (в ней производная не существует). Каково же поведение графика функции в окрестности такой точки? График функции  приведен на рисунке слева. В начале координат виден излом графика. Касательной к графику в начале координат не существует. Единственная критическая точка приведен на рисунке слева. В начале координат виден излом графика. Касательной к графику в начале координат не существует. Единственная критическая точка  есть точка минимума функции (что видно из приведенного графика). есть точка минимума функции (что видно из приведенного графика).
  Не следует думать, что любая критическая точка функции даёт либо максимум, либо минимум. В некоторых критических точках экстремума может не оказаться вовсе. Параллельность к оси Не следует думать, что любая критическая точка функции даёт либо максимум, либо минимум. В некоторых критических точках экстремума может не оказаться вовсе. Параллельность к оси  касательной к графику в некоторой его точке с координатой касательной к графику в некоторой его точке с координатой  (что эквивалентно выполнению условия (что эквивалентно выполнению условия  ) не обязательно делает эту точку точкой максимума или минимума. Пример подобной ситуации представлен на рисунке. Для соответствующей функции точка ) не обязательно делает эту точку точкой максимума или минимума. Пример подобной ситуации представлен на рисунке. Для соответствующей функции точка  является критической (точнее, стационарной), так как касательная к графику в соответствующей точке параллельна оси Ох (а потому является критической (точнее, стационарной), так как касательная к графику в соответствующей точке параллельна оси Ох (а потому  ). Однако, как видно из графика, точка ). Однако, как видно из графика, точка  не является ни точкой максимума, ни точкой минимума. В качестве примера конкретной функции с таким свойством можно привести функцию не является ни точкой максимума, ни точкой минимума. В качестве примера конкретной функции с таким свойством можно привести функцию  , график которой изображен на рисунке слева. Ее производная , график которой изображен на рисунке слева. Ее производная  обращается в 0, очевидно, при обращается в 0, очевидно, при  . Поэтому . Поэтому  – стационарная точка функции (касательная к кубической параболе – стационарная точка функции (касательная к кубической параболе  в начале координат просто совпадает с осью в начале координат просто совпадает с осью  − см. рисунок), но экстремума в этой точке, очевидно, нет. − см. рисунок), но экстремума в этой точке, очевидно, нет.
Из сказанного выше повторим 2 основных вывода.
1. Все экстремумы находятся среди критических точек.
2. Не всякая критическая точка является точкой экстремума.
Отсюда следует, что для нахождения экстремума функции необходимо решить 2 задачи:
а) все найти критические точки функции,
б) исследовать каждую из них на наличие в них экстремума (максимума или минимума).
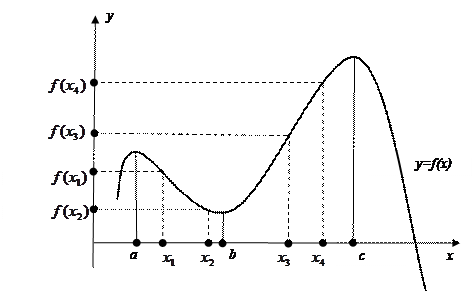
Первая задача решается вычислением выражения для производной функции, с помощью которого находятся критические точки функции. Для решения второй задачи необходимо понять, что отличает критическую точку, в которой экстремум есть, от критической точки, в которой экстремума нет. Обратимся к функции, график которой изображен на рисунке ниже. 
У этой функции 4 критических точки:  , ,  , ,  и и  . В первых трех экстремумы есть (соответственно максимум, минимум, снова максимум), а в последней нет. Можно заметить, что при переходе через точку . В первых трех экстремумы есть (соответственно максимум, минимум, снова максимум), а в последней нет. Можно заметить, что при переходе через точку  (точку максимума) функция от возрастания перешла к убыванию (то же самое можно сказать и о другой точке максимума (точку максимума) функция от возрастания перешла к убыванию (то же самое можно сказать и о другой точке максимума  ), а при переходе через точку ), а при переходе через точку  (точку минимума) функция от убывания переходит к возрастанию. При переходе же через критическую точку (точку минимума) функция от убывания переходит к возрастанию. При переходе же через критическую точку  (в которой экстремума нет) характер монотонности функции не меняется (как убывала, так и продолжает убывать). Это и отличает критические точки с экстремумами от критических точек без таковых. На основании этих рассуждений можно сформулировать следующее утверждение. (в которой экстремума нет) характер монотонности функции не меняется (как убывала, так и продолжает убывать). Это и отличает критические точки с экстремумами от критических точек без таковых. На основании этих рассуждений можно сформулировать следующее утверждение.
Теорема (достаточное условие экстремума; проверка критической точки на экстремум). Пусть  – критическая точка функции – критическая точка функции  . Тогда если при переходе через точку . Тогда если при переходе через точку  функция: а) от возрастания переходит к убыванию, то функция: а) от возрастания переходит к убыванию, то  – точка максимума; б) от убывания переходит к возрастанию, то – точка максимума; б) от убывания переходит к возрастанию, то  – точка минимума; в) не меняет характера монотонности (продолжает убывать или продолжает возрастать), то в – точка минимума; в) не меняет характера монотонности (продолжает убывать или продолжает возрастать), то в  экстремума нет. экстремума нет.
Пример 2. Опять обратимся к простой функции  . Эта функция в качестве примера снова выбрана потому, что хорошо известен ее график (парабола, см. рисунок). Поэтому, не пользуясь приведенной теоремой, можно сказать, что . Эта функция в качестве примера снова выбрана потому, что хорошо известен ее график (парабола, см. рисунок). Поэтому, не пользуясь приведенной теоремой, можно сказать, что  – точка минимума, других точек экстремума нет. Попробуем получить этот же результат с помощью приведенной теоремы, не обращаясь к графику. Сначала ищем критические точки. Имеем – точка минимума, других точек экстремума нет. Попробуем получить этот же результат с помощью приведенной теоремы, не обращаясь к графику. Сначала ищем критические точки. Имеем  , а потому , а потому  . Понятно, что выражение . Понятно, что выражение  вычислимо при любых вычислимо при любых  , а потому производная существует везде. Найдем стационарные точки (в которых производная обращается в 0): , а потому производная существует везде. Найдем стационарные точки (в которых производная обращается в 0):  . Поэтому точка . Поэтому точка  – единственная критическая точка. Проверим ее на наличие экстремума. При переходе через эту точку убывание функции меняется на возрастание (участки монотонности этой функции мы, не обращаясь к графику, нашли ранее тоже с помощью производной: – единственная критическая точка. Проверим ее на наличие экстремума. При переходе через эту точку убывание функции меняется на возрастание (участки монотонности этой функции мы, не обращаясь к графику, нашли ранее тоже с помощью производной: 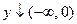 и и  ). По приведенной выше теореме точка ). По приведенной выше теореме точка  действительно точка минимума функции. действительно точка минимума функции.
 Пример 3: Исследовать на монотонность и экстремумы функцию Пример 3: Исследовать на монотонность и экстремумы функцию 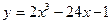 . .
Решение такого типа примеров удобнее находить по следующей схеме.
1. Находим производную  . Выражение для производной опять получилось таким, что можно вычислить его значение при любом . Выражение для производной опять получилось таким, что можно вычислить его значение при любом  . Поэтому производная опять существует для всех чисел, а потому все критические точки функции могут быть только ее стационарными точками (т.е. точками, в которых эта производная обращается в ноль). Для удобства нахождения таких точек можно попробовать разложить выражение для производной на множители до тех пор, пока это возможно: . Поэтому производная опять существует для всех чисел, а потому все критические точки функции могут быть только ее стационарными точками (т.е. точками, в которых эта производная обращается в ноль). Для удобства нахождения таких точек можно попробовать разложить выражение для производной на множители до тех пор, пока это возможно:  , ,  . .
 2. Находим критические точки: 2. Находим критические точки: 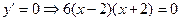 . Таким образом, для нахождения критических точек надо решить уравнение . Таким образом, для нахождения критических точек надо решить уравнение  . Поскольку левая часть уравнения представляет собой произведение трех множителей (это 6, . Поскольку левая часть уравнения представляет собой произведение трех множителей (это 6,  и и  ), то она может обратиться в 0 только при тех числах ), то она может обратиться в 0 только при тех числах  , которые обратят в 0 хотя бы один их сомножителей. Число 6 ни при каких значениях , которые обратят в 0 хотя бы один их сомножителей. Число 6 ни при каких значениях  в 0 не обратится (оно на в 0 не обратится (оно на  вообще внимания не обращает). А вот множители вообще внимания не обращает). А вот множители  и и  обращаются в 0 (соответственно при обращаются в 0 (соответственно при  и и  ), зануляя тем самым при этих ), зануляя тем самым при этих  всю левую часть уравнения. Таким образом, у уравнения всю левую часть уравнения. Таким образом, у уравнения  всего два корня: всего два корня:  и и  , которые и являются критическими точками исследуемой функции. , которые и являются критическими точками исследуемой функции.
3. Наносим критические точки на числовую прямую и определяем знаки производной на получившихся интервалах. В нашем примере получились интервалы  , ,  , ,  . .  Критические точки разбивают числовую прямую на интервалы, внутри каждого из которых производная имеет один и тот же знак (вспомните метод интервалов решения неравенств). Поэтому для определения знака производной на каждом получившемся интервале достаточно вычислить значение производной в любой «пробной» точке из этого интервала и получившийся знак «+» или «−» поставить над всем интервалом. Для интервала Критические точки разбивают числовую прямую на интервалы, внутри каждого из которых производная имеет один и тот же знак (вспомните метод интервалов решения неравенств). Поэтому для определения знака производной на каждом получившемся интервале достаточно вычислить значение производной в любой «пробной» точке из этого интервала и получившийся знак «+» или «−» поставить над всем интервалом. Для интервала  в качестве пробной точки можно взять, например, в качестве пробной точки можно взять, например,  и подставить его в выражение для производной и подставить его в выражение для производной  : :
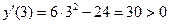 . Поэтому на всем интервале . Поэтому на всем интервале  производная положительна (ставим «+» над соответствующим интервалом). Аналогично, для интервала производная положительна (ставим «+» над соответствующим интервалом). Аналогично, для интервала  берем пробную точку берем пробную точку  : :  . Поэтому над всем интервалом ставим знак «−». Для интервала . Поэтому над всем интервалом ставим знак «−». Для интервала  считаем считаем  , ставим «+» над интервалом. , ставим «+» над интервалом.
4. Строим итоговую таблицу, по которой потом будем писать ответ к этому примеру. В первой ее строчке заносим интервалы с граничными критическими точками. Во второй строке расставляем получившиеся знаки производной на интервалах. В третьей получаем выводы об интервалах монотонности и точках экстремума.
Последняя строчка таблицы заполнялась следующим образом. По второму столбцу: на интервале  знак производной «+», поэтому функция возрастает (поставлена стрелка знак производной «+», поэтому функция возрастает (поставлена стрелка  ). По четвертому столбцу: на интервале ). По четвертому столбцу: на интервале  знак производной «−», поэтому функция убывает (поставлена стрелка знак производной «−», поэтому функция убывает (поставлена стрелка  ). По шестому столбцу: на интервале ). По шестому столбцу: на интервале  знак производной «+», поэтому функция возрастает (поставлена стрелка знак производной «+», поэтому функция возрастает (поставлена стрелка  ). Рассмотрим критическую точку ). Рассмотрим критическую точку  . Из таблицы видно, что при переходе через эту точку функция от возрастания переходит к убыванию. Поэтому . Из таблицы видно, что при переходе через эту точку функция от возрастания переходит к убыванию. Поэтому  − точка максимума исходной функции − точка максимума исходной функции 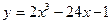 . Чтобы найти само максимальное значение, надо вычислить значение этой функции в точке максимума . Чтобы найти само максимальное значение, надо вычислить значение этой функции в точке максимума  : :  . Рассмотрим критическую точку . Рассмотрим критическую точку  . Из таблицы видно, что при переходе через эту точку функция от убывания переходит к возрастанию. Поэтому . Из таблицы видно, что при переходе через эту точку функция от убывания переходит к возрастанию. Поэтому  − точка минимума исходной функции − точка минимума исходной функции 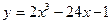 . Чтобы найти само минимальное значение, надо вычислить значение этой функции в точке минимума . Чтобы найти само минимальное значение, надо вычислить значение этой функции в точке минимума  : :  . .
Ответ:  , ,  , ,  ; ;  точка максимума, точка максимума,  ; ;  точка минимума, точка минимума,  . .
Пример 4: Исследовать на монотонность и экстремумы функцию  . .
Решение проведем по той схеме, описанной при решении предыдущего примера.
1. Находим производную  . Выражение для производной опять можно вычислить при любом . Выражение для производной опять можно вычислить при любом  , а потому все критические точки функции могут быть только ее стационарными точками (т.е. точками, в которых эта производная обращается в ноль). Для их поиска раскладываем полученное выражение на множители до тех пор, пока это возможно: , а потому все критические точки функции могут быть только ее стационарными точками (т.е. точками, в которых эта производная обращается в ноль). Для их поиска раскладываем полученное выражение на множители до тех пор, пока это возможно:  , ,  . .
2. Находим критические точки: 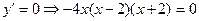 . Поскольку левая часть уравнения представляет собой произведение пяти сомножителей (это: . Поскольку левая часть уравнения представляет собой произведение пяти сомножителей (это:  , ,  , ,  и и  ), то она может обратиться в 0 только при тех числах ), то она может обратиться в 0 только при тех числах  , которые обратят в 0 хотя бы один их сомножителей. Поэтому у уравнения , которые обратят в 0 хотя бы один их сомножителей. Поэтому у уравнения  всего три корня: всего три корня:  , ,  , ,  , которые и являются критическими точками исследуемой функции. , которые и являются критическими точками исследуемой функции.
3. Наносим критические точки на числовую прямую и определяем знаки
 производной на получившихся интервалах. В нашем примере получились такие четыре интервала: производной на получившихся интервалах. В нашем примере получились такие четыре интервала:  , ,  , ,  , ,  . .  Для определения знака производной на каждом получившемся интервале снова используем вычисление производной в пробных точках. Для интервала Для определения знака производной на каждом получившемся интервале снова используем вычисление производной в пробных точках. Для интервала  в качестве пробной точки можно взять, например, в качестве пробной точки можно взять, например,  : :
 . Поэтому на всем интервале . Поэтому на всем интервале  производная отрицательна. Для интервала производная отрицательна. Для интервала  берем пробную точку берем пробную точку  : :  . Поэтому над всем интервалом ставим знак «+». Для интервала . Поэтому над всем интервалом ставим знак «+». Для интервала  берем пробную точку берем пробную точку  : :  . Поэтому над всем интервалом ставим знак «−». Для интервала . Поэтому над всем интервалом ставим знак «−». Для интервала  считаем считаем  , ставим «+» над интервалом. , ставим «+» над интервалом.
4. Строим итоговую таблицу (аналогичную построенной для предыдущего примера). В первой ее строчке заносим интервалы с граничными критическими точками. Во второй строке расставляем получившиеся знаки производной на интервалах. В третьей получаем выводы об интервалах монотонности и точках экстремума.
|



 состоит в том, что она помогает исследованию самой функции
состоит в том, что она помогает исследованию самой функции  , т.е. исследованию характера зависимости переменной
, т.е. исследованию характера зависимости переменной  от переменной
от переменной  , выраженного соотношением
, выраженного соотношением  и ждем соответствующий урожай в количестве
и ждем соответствующий урожай в количестве 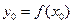 . Пусть появилась возможность дополнительно внести удобрения в количестве
. Пусть появилась возможность дополнительно внести удобрения в количестве  единиц. Стоит ли это делать? Будет ли урожай больше или мы уже внесли столь много удобрений, что дальнейшее увеличение его количества только нанесет вред урожаю? Вопрос сводится к следующему: будет ли при увеличении аргумента
единиц. Стоит ли это делать? Будет ли урожай больше или мы уже внесли столь много удобрений, что дальнейшее увеличение его количества только нанесет вред урожаю? Вопрос сводится к следующему: будет ли при увеличении аргумента 
 оси
оси  вверх. Попробуем разобраться, как это сказывается на характере зависимости
вверх. Попробуем разобраться, как это сказывается на характере зависимости  и
и  из интервала
из интервала  и
и  функции
функции 
 и
и  из интервала
из интервала  на оси
на оси  , а потому
, а потому  . Естественно назвать такой интервал интервалом возрастания функции
. Естественно назвать такой интервал интервалом возрастания функции  – функция )
– функция )  – функция
– функция  таковым не будет, так как на одной его части функция убывает, а на другой возрастает. Как же находить интервалы монотонности? Конечно, если имеется график функции, то эти интервалы просто видны. Но чаще всего графика нет, а есть только формула
таковым не будет, так как на одной его части функция убывает, а на другой возрастает. Как же находить интервалы монотонности? Конечно, если имеется график функции, то эти интервалы просто видны. Но чаще всего графика нет, а есть только формула  . В этом случае опять помогает производная. Обратимся к рисункам.
. В этом случае опять помогает производная. Обратимся к рисункам.

 с осью
с осью  . Поскольку тангенсы острых углов положительны, то
. Поскольку тангенсы острых углов положительны, то  . Аналогично, берем произвольную точку
. Аналогично, берем произвольную точку  . Поскольку тангенсы тупых углов отрицательны, то
. Поскольку тангенсы тупых углов отрицательны, то  . Итак, мы наглядно убедились в том, что если функция возрастает на некотором интервале, то во всех точках этого интервала производная (если она существует) положительна (возможно, обращаясь в некоторых точках в 0), а во всех точках интервала убывания производная отрицательна. Справедлива соответствующая
. Итак, мы наглядно убедились в том, что если функция возрастает на некотором интервале, то во всех точках этого интервала производная (если она существует) положительна (возможно, обращаясь в некоторых точках в 0), а во всех точках интервала убывания производная отрицательна. Справедлива соответствующая (соответственно,
(соответственно,  ) для всех значений
) для всех значений  Пример 1. Найти промежутки монотонности функции
Пример 1. Найти промежутки монотонности функции  .
.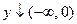 и
и  . Попробуем получить этот же результат с помощью приведенной теоремы, не обращаясь к графику. В нашем примере
. Попробуем получить этот же результат с помощью приведенной теоремы, не обращаясь к графику. В нашем примере  , а потому
, а потому  . Понятно, что выражение
. Понятно, что выражение  для производной положительно для всех положительных х и отрицательно для всех отрицательных. Поэтому производная
для производной положительно для всех положительных х и отрицательно для всех отрицательных. Поэтому производная  для отрицательных
для отрицательных  для положительных
для положительных 
 больше (соответственно, меньше) значений функции в ближайших к
больше (соответственно, меньше) значений функции в ближайших к  имеется график функции, то снова проблем не возникает – достаточно спроектировать на ось
имеется график функции, то снова проблем не возникает – достаточно спроектировать на ось  ,
,  ,
,  . Итак, мы получили, что в точках экстремума производная обращается в 0 (если она, конечно, в этих точках вообще существует). Этот факт выражает следующая
. Итак, мы получили, что в точках экстремума производная обращается в 0 (если она, конечно, в этих точках вообще существует). Этот факт выражает следующая . Тогда если
. Тогда если  .
. . Эта функция непрерывна на всей числовой прямой. Найдем выражение для производной этой функции:
. Эта функция непрерывна на всей числовой прямой. Найдем выражение для производной этой функции:  . Стационарных точек у функции нет (числитель дроби не обращается в 0 ни при каких значениях
. Стационарных точек у функции нет (числитель дроби не обращается в 0 ни при каких значениях 
 производная не существует (делить на 0 нельзя). Поэтому
производная не существует (делить на 0 нельзя). Поэтому 
 Не следует думать, что любая критическая точка функции даёт либо максимум, либо минимум. В некоторых критических точках экстремума может не оказаться вовсе. Параллельность к оси
Не следует думать, что любая критическая точка функции даёт либо максимум, либо минимум. В некоторых критических точках экстремума может не оказаться вовсе. Параллельность к оси  , график которой изображен на рисунке слева. Ее производная
, график которой изображен на рисунке слева. Ее производная  обращается в 0, очевидно, при
обращается в 0, очевидно, при  . Поэтому
. Поэтому 
 . Поэтому точка
. Поэтому точка  ). По приведенной выше теореме точка
). По приведенной выше теореме точка  Пример 3: Исследовать на монотонность и экстремумы функцию
Пример 3: Исследовать на монотонность и экстремумы функцию 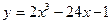 .
. . Выражение для производной опять получилось таким, что можно вычислить его значение при любом
. Выражение для производной опять получилось таким, что можно вычислить его значение при любом  ,
,  .
. 2. Находим критические точки:
2. Находим критические точки: 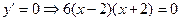 . Таким образом, для нахождения критических точек надо решить уравнение
. Таким образом, для нахождения критических точек надо решить уравнение  . Поскольку левая часть уравнения представляет собой произведение трех множителей (это 6,
. Поскольку левая часть уравнения представляет собой произведение трех множителей (это 6,  и
и  ), то она может обратиться в 0 только при тех числах
), то она может обратиться в 0 только при тех числах  и
и  ), зануляя тем самым при этих
), зануляя тем самым при этих  и
и  , которые и являются критическими точками исследуемой функции.
, которые и являются критическими точками исследуемой функции. ,
,  ,
,  .
.  Критические точки разбивают числовую прямую на интервалы, внутри каждого из которых производная имеет один и тот же знак (вспомните метод интервалов решения неравенств). Поэтому для определения знака производной на каждом получившемся интервале достаточно вычислить значение производной в любой «пробной» точке из этого интервала и получившийся знак «+» или «−» поставить над всем интервалом. Для интервала
Критические точки разбивают числовую прямую на интервалы, внутри каждого из которых производная имеет один и тот же знак (вспомните метод интервалов решения неравенств). Поэтому для определения знака производной на каждом получившемся интервале достаточно вычислить значение производной в любой «пробной» точке из этого интервала и получившийся знак «+» или «−» поставить над всем интервалом. Для интервала  и подставить его в выражение для производной
и подставить его в выражение для производной 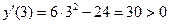 . Поэтому на всем интервале
. Поэтому на всем интервале  . Поэтому над всем интервалом ставим знак «−». Для интервала
. Поэтому над всем интервалом ставим знак «−». Для интервала  , ставим «+» над интервалом.
, ставим «+» над интервалом.




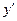





 . Из таблицы видно, что при переходе через эту точку функция от возрастания переходит к убыванию. Поэтому
. Из таблицы видно, что при переходе через эту точку функция от возрастания переходит к убыванию. Поэтому  . Рассмотрим критическую точку
. Рассмотрим критическую точку  .
. ,
,  ,
,  ;
;  ;
;  .
. .
. . Выражение для производной опять можно вычислить при любом
. Выражение для производной опять можно вычислить при любом  ,
,  .
.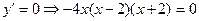 . Поскольку левая часть уравнения представляет собой произведение пяти сомножителей (это:
. Поскольку левая часть уравнения представляет собой произведение пяти сомножителей (это:  ,
,  всего три корня:
всего три корня:  ,
,  ,
,  , которые и являются критическими точками исследуемой функции.
, которые и являются критическими точками исследуемой функции. производной на получившихся интервалах. В нашем примере получились такие четыре интервала:
производной на получившихся интервалах. В нашем примере получились такие четыре интервала:  ,
,  ,
,  . Поэтому на всем интервале
. Поэтому на всем интервале  берем пробную точку
берем пробную точку  :
:  . Поэтому над всем интервалом ставим знак «+». Для интервала
. Поэтому над всем интервалом ставим знак «+». Для интервала  берем пробную точку
берем пробную точку  :
:  . Поэтому над всем интервалом ставим знак «−». Для интервала
. Поэтому над всем интервалом ставим знак «−». Для интервала  , ставим «+» над интервалом.
, ставим «+» над интервалом.


