
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раскрытие неопределенностей в пределахСодержание книги
Поиск на нашем сайте
Рассмотрим теперь способы избавления от истинных неопределенностей типа 1. Предел отношения многочленов: Пример 1. Пример 2. Пример 3. 2. Предел отношения многочленов на бесконечности: В этом случае неопределенность исчезает, если разделить числитель и знаменатель на старшую степень знаменателя (т.е. на Пример 4. Пример 5. 3. Пределы с корнями: В числителе и/или в знаменателе стоит сумма или разность выражений, содержащих корни (квадратные, кубичные …). В случае квадратных корней можно домножить числитель и знаменатель на так называемое сопряженное выражение к числителю и/или знаменателю (сумму или разность корней домножить на их разность или сумму соответственно), после этого воспользоваться формулой разности квадратов: Пример 7. Пример 8. Пример 9. Мы прошли лишь некоторые приемы избавления от неопределенностей в пределах. Подобных приемов гораздо больше, но все они «работают» лишь для конкретных классов функций и видах неопределенности. В дальнейшем (после прохождения производных) будет дан практически универсальный прием избавления от неопределенностей в пределах (так называемое «правило Лопиталя»).
Замечательные пределы В истории математики некоторые пределы играли достаточно важную роль, однако, их вычисление не могло быть проведено привычными приемами (например, перечисленными выше), а потому для их вычисления использовались достаточно громоздкие построения и рассуждения. Эти пределы впоследствии были названы замечательными. Мы не будем проводить соответствующие доказательства, поскольку в дальнейшем появится упомянутый выше универсальный способ вычисления пределов (с помощью производных), которым вычисляются замечательные и многие другие пределы. 1. 2. Число е (точнее, второй замечательный предел, который это число определяет), возникает естественным образом и в ряде практических задач. Например, в задаче о банковский процентах. Прежде, чем ее изложить, напомним понятие процента. Один процент от некоторого числа а есть сотая часть этого числа: {1 % от числа а } = (*) увеличение числа на р% означает умножение его на выражение А теперь обещанная Задача о банковских процентах. Банк дает 100 % годовых (для простоты), а на другой срок − пропорционально длительности срока ( 1. Первая стратегий − самая ленивая: кладем деньги в банк и ждем год. Тогда в конце года сумма, очевидно, удвоится: 2. Вторая стратегия: кладем в банк наши а рублей на полгода, после чего изымаем ее вместе с набежавшими процентами, а затем тут же все эти деньги кладем обратно в банк на оставшиеся полгода. Через первые полгода снятая сумма, согласно правилу (*) (где р=50 %), будет равна 3. Берем с процентами и снова кладем каждый месяц. В конце первого месяца получим сумму (которую сразу же положим на следующий месяц), равную 4. Берем-кладем каждый день. В конце года получим сумму, равную Таким образом, чем чаще мы бегаем в банк и «капитализируем» накопившуюся сумму, тем больший доход в конце года мы получаем. Коэффициент увеличения вклада к концу года принимал следующие все возрастающие значения: 2, Точно так же можно получить общую формулу: если банк дает Р % годовых, то при непрерывном процессе «капитализации» вклада за t лет сумма вклада будет равна
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.146.108 (0.011 с.) |

 . Первый способ следующий. Если при вычислении
. Первый способ следующий. Если при вычислении  возникают указанные выше неопределенности, то можно попробовать тождественно преобразовать выражение, задающее функцию
возникают указанные выше неопределенности, то можно попробовать тождественно преобразовать выражение, задающее функцию  , таким образом, чтобы неопределенности (при подстановке
, таким образом, чтобы неопределенности (при подстановке  в преобразованное выражение) уже не возникало. Вся сложность этого способа в том, как научиться находить такое тождественное преобразование. Однако для определенных классов функций и типов получающихся неопределенностей такие преобразования известны. Рассмотрим некоторые из них.
в преобразованное выражение) уже не возникало. Вся сложность этого способа в том, как научиться находить такое тождественное преобразование. Однако для определенных классов функций и типов получающихся неопределенностей такие преобразования известны. Рассмотрим некоторые из них. .
. 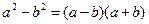 ,
,  ,
,  ;
; , где
, где  и
и  − корни квадратного уравнения
− корни квадратного уравнения  .
.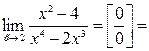
 =
=  =
=  =
=  ;
;
 =
=  =
=  ;
;
 :
:  ,
,  , а потому
, а потому  } =
} =  =
=  .
. .
. , так как в знаменателе многочлен степени n).
, так как в знаменателе многочлен степени n).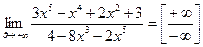


 {если формально подставить
{если формально подставить  в выражение после знака предела, то в дробях
в выражение после знака предела, то в дробях  ,
,  ,
,  ,
,  и
и  получится
получится  ; в соответствии с рассмотренным выше «первым правилом псевдонеопределенности» это означает стремление этих дробей к 0, что в дальнейшем обозначим для наглядности значком
; в соответствии с рассмотренным выше «первым правилом псевдонеопределенности» это означает стремление этих дробей к 0, что в дальнейшем обозначим для наглядности значком  } =
} =  .
.
 =
= 
 =
=  =
=  . Пример 6.
. Пример 6. 
 =
=  =
=  .
. .
.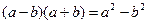 . Если же участвуют корни третьей степени, то домножать числитель и знаменатель необходимо на неполный квадрат суммы-разности корней для образования формулы суммы-разности кубов:
. Если же участвуют корни третьей степени, то домножать числитель и знаменатель необходимо на неполный квадрат суммы-разности корней для образования формулы суммы-разности кубов:  . После применения этих формул корни исчезают, либо входят уже в такие выражения, которые не ведут к неопределенности при вычислении предела.
. После применения этих формул корни исчезают, либо входят уже в такие выражения, которые не ведут к неопределенности при вычислении предела. = {квадратный корень содержится в числителе в разности
= {квадратный корень содержится в числителе в разности  , поэтому домножим числитель и знаменатель на соответствующую сумму
, поэтому домножим числитель и знаменатель на соответствующую сумму  и применим формулу
и применим формулу  =
=  =
=  =
=  =
=  = {после сокращения на
= {после сокращения на  } =
} = 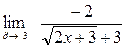 ={подставляя
={подставляя  } =
} =  .
. = {квадратный корень содержится в знаменателе в разности
= {квадратный корень содержится в знаменателе в разности 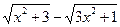 , поэтому домножим числитель и знаменатель на соответствующую сумму
, поэтому домножим числитель и знаменатель на соответствующую сумму  и применим формулу
и применим формулу  =
=  =
= 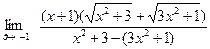 =
= 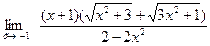 =
=  =
=  =
=  = {подставляя
= {подставляя  }
}  .
. = {кубичный корень содержится в числителе в сумме
= {кубичный корень содержится в числителе в сумме  , поэтому домножим числитель и знаменатель на неполный квадрат разности
, поэтому домножим числитель и знаменатель на неполный квадрат разности 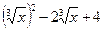 и применим формулу
и применим формулу  } =
} =  =
=  =
= 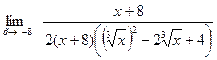 =
=  .
. − первый замечательный предел.
− первый замечательный предел. − второй замечательный предел. Этот предел является определением «замечательного» числа е. Это число играет в математике не меньшую роль, чем известное число
− второй замечательный предел. Этот предел является определением «замечательного» числа е. Это число играет в математике не меньшую роль, чем известное число  .
. . Тогда р % от числа а, естественно, в р раз больше: { р% от числа а } =
. Тогда р % от числа а, естественно, в р раз больше: { р% от числа а } =  . Посмотрим, к какому числу
. Посмотрим, к какому числу 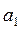 мы придем, если увеличим число
мы придем, если увеличим число  на р%:
на р%:  . Поэтому получаем правило:
. Поэтому получаем правило: .
. года – 50 %; 1 месяц –
года – 50 %; 1 месяц –  %; 1 день –
%; 1 день – 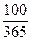 % и так далее). Задача заключается в том, чтобы выработать такую стратегию взаимоотношений с банком в течение года, чтобы, имея начальную сумму в а рублей, получить в конце года максимальную прибыль. Сравним различные стратегии вкладов с начальной суммой
% и так далее). Задача заключается в том, чтобы выработать такую стратегию взаимоотношений с банком в течение года, чтобы, имея начальную сумму в а рублей, получить в конце года максимальную прибыль. Сравним различные стратегии вкладов с начальной суммой 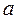 рублей и будем следить за суммой вклада в конце года.
рублей и будем следить за суммой вклада в конце года. ;
;  .
. . В конце года полученная сумма опять увеличится на 50 %, а потому, согласно правилу (*), мы получим:
. В конце года полученная сумма опять увеличится на 50 %, а потому, согласно правилу (*), мы получим:  ;
;  .
. . Тогда в конце года получим
. Тогда в конце года получим  ;
; 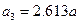 .
. ;
;  .
. ,
,  ,
,  . А если бегать в банк каждый час? Каждую минуту? Возникает вопрос, возможно ли безграничное увеличение коэффициента умножения вклада при все учащающихся актах капитализации вклада? Сначала мы условно делили год на 2 части и, соответственно, капитализировали вклад каждые полгода (коэффициент умножения получался
. А если бегать в банк каждый час? Каждую минуту? Возникает вопрос, возможно ли безграничное увеличение коэффициента умножения вклада при все учащающихся актах капитализации вклада? Сначала мы условно делили год на 2 части и, соответственно, капитализировали вклад каждые полгода (коэффициент умножения получался 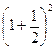 ); потом мы делили год на 12 частей и, соответственно, капитализировали вклад каждый месяц (коэффициент умножения получался
); потом мы делили год на 12 частей и, соответственно, капитализировали вклад каждый месяц (коэффициент умножения получался  ); затем мы делили год на 365 частей и, соответственно, капитализировали вклад каждый день (коэффициент умножения получался
); затем мы делили год на 365 частей и, соответственно, капитализировали вклад каждый день (коэффициент умножения получался  ). Теперь видна общая формула: если бы мы поделили год на
). Теперь видна общая формула: если бы мы поделили год на  частей и соответствующим образом установили частоту капитализации вкладов, то коэффициент умножения вклада к концу года оказался бы равным
частей и соответствующим образом установили частоту капитализации вкладов, то коэффициент умножения вклада к концу года оказался бы равным  . Будет ли этот коэффициент безгранично расти при безграничном увеличении
. Будет ли этот коэффициент безгранично расти при безграничном увеличении  ? Однако слева получился второй замечательный предел, а потому
? Однако слева получился второй замечательный предел, а потому  . Поэтому надеяться на безграничное увеличение вклада не приходится. Теперь понятно, что в идеале (при переходе процесса капитализации в непрерывный) максимальный коэффициент увеличения вклада равен
. Поэтому надеяться на безграничное увеличение вклада не приходится. Теперь понятно, что в идеале (при переходе процесса капитализации в непрерывный) максимальный коэффициент увеличения вклада равен  . В этом (ясно, что нереализуемом) случае в конце года мы получим
. В этом (ясно, что нереализуемом) случае в конце года мы получим  рублей. Легко посчитать (попробуйте сделать это сами), что в этом случае годовое увеличение вклада составит 171.8 % (вместо обещанных банком 100 %).
рублей. Легко посчитать (попробуйте сделать это сами), что в этом случае годовое увеличение вклада составит 171.8 % (вместо обещанных банком 100 %). . Эта формула носит название формулы непрерывных процентов.
. Эта формула носит название формулы непрерывных процентов.


