
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функции и построения графикаСодержание книги
Поиск на нашем сайте
Мы изучили все необходимые способы исследования функций. Соберем изученное вместе и получится следующая Схема исследования функции (после выполнения каждого пункта заносим полученную информацию в эскиз будущего графика). 1) Находим область определения функции 2) Проверяем функцию на четность или нечетность. Это сводится к проверке симметричности найденной области определения относительно нуля, затем проверке равенства 3) Проверяем функцию на периодичность. В этом есть смысл в том случае, если формула, задающая функцию, содержит тригонометрический функции. Иначе периодичности нет, разве только в специально придуманных примерах. График периодической функции повторяет себя при сдвиге на величину периода Т вправо и влево вдоль оси 4) Находим (если это не слишком сложно) точки пересечения графика с осями координат. Для нахождения точки пересечения с осью у необходимо вычислить значение функции в нуле 5) Найти асимптоты (наклонные и вертикальные) графика исследуемой функции. Нарисовать соответствующие прямые на эскизе будущего графика. 6) Найти участки монотонности и экстремумы функции. Отметить на эскизе точки графика, соответствующие максимумам и минимумам. 7) Исследовать направления выпуклости графика функции и найти точки его перегиба. Отметить точки перегиба на эскизе графика. 8) Строить эскиз графика по полученной информации. Пример. Исследовать функцию Идем по изложенной выше схеме. В нашем примере 1) Область определения. Формула, задающая функцию, предполагает при вычислении ее значений следующие операции: возведение в квадрат, сложение, вычитание и деление. Только одна из них (деление) имеет ограничение (на 0 делить нельзя). Поэтому в область определения не входят те числа 2) Четность-нечетность. Найденная область определения не симметрична относительно нуля 3) Функция не периодическая (не содержит тригонометрических функций, а пример не придуман специально, чтобы запутать нас в этом пункте). 4) Точки пересечения с осями. а) С осью у: б) С осью 5) Асимптоты. Найдем наклонную асимптоту с уравнением
Подставляем найденные значения параметров 6) Монотонность и экстремумы.
Обратим внимание на то, что минимальное значение функции (точнее, значение функции в точке минимума) больше максимального (точнее, значения функции в точке максимума). Это часто встречается, когда функция имеет точки разрыва (наша функция имеет точку разрыва второго рода 7) Выпуклость и точки перегиба. Ищем критические точки графика. Находим вторую производную:
8) Достраиваем окончательно эскиз графика по полученной выше информации (см. рисунок).
Для закрепления материала постройте графики функций
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.011 с.) |

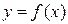 и построения ее графика
и построения ее графика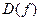 . Если в нее не вошли отдельные числа, то выкалываем их (обводим кружком) на оси
. Если в нее не вошли отдельные числа, то выкалываем их (обводим кружком) на оси  на эскизе графика.
на эскизе графика. для четной функции и
для четной функции и  для нечетной. Если функция оказалась четной (нечетной), то ее график должен получиться симметричным относительно оси у (относительно начала координат).
для нечетной. Если функция оказалась четной (нечетной), то ее график должен получиться симметричным относительно оси у (относительно начала координат). .
.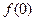 (если, конечно, 0 входит в область определения функции – иначе точки пересечения с осью у нет) и отметить полученное число на оси у. Для нахождения точек пересечения с осью
(если, конечно, 0 входит в область определения функции – иначе точки пересечения с осью у нет) и отметить полученное число на оси у. Для нахождения точек пересечения с осью 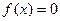 и отметить получившиеся корни на оси
и отметить получившиеся корни на оси  и построить ее график.
и построить ее график.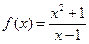 .
. . Итак,
. Итак,  .
.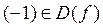 , а симметричное число
, а симметричное число  ). Поэтому нет ни четности, ни нечетности. Функция общего положения.
). Поэтому нет ни четности, ни нечетности. Функция общего положения.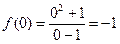 ; отмечаем на оси у точку (–1) как точку пересечения графика с этой осью.
; отмечаем на оси у точку (–1) как точку пересечения графика с этой осью. корней не имеет (дробь может быть равна нулю при тех
корней не имеет (дробь может быть равна нулю при тех  строго положительно для всех
строго положительно для всех 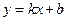 при
при  . Ищем значения параметров
. Ищем значения параметров  и
и  по приводимым выше формулам:
по приводимым выше формулам: ,
, .
. есть уравнение наклонной асимптоты графика при
есть уравнение наклонной асимптоты графика при  .
. 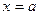 , причем число
, причем число  может лежать только на границе области определения функции. Поскольку область определения функции есть
может лежать только на границе области определения функции. Поскольку область определения функции есть  , то граничной точкой такой области является только число 1. Поэтому проверяем только
, то граничной точкой такой области является только число 1. Поэтому проверяем только  . Это значит, что проверяется на вертикальную асимптоту прямая с уравнением
. Это значит, что проверяется на вертикальную асимптоту прямая с уравнением  . Считаем односторонние (правый и левый) пределы при
. Считаем односторонние (правый и левый) пределы при  :
:  . Дробь
. Дробь  означает, что при подстановке вместо
означает, что при подстановке вместо 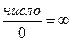 . Осталось выяснить знак этой бесконечности. При
. Осталось выяснить знак этой бесконечности. При  . Итак, получили
. Итак, получили  ,
,  . Так как оба односторонних предела равны бесконечности, то (по определению) прямая с уравнением
. Так как оба односторонних предела равны бесконечности, то (по определению) прямая с уравнением  Находим производную:
Находим производную: 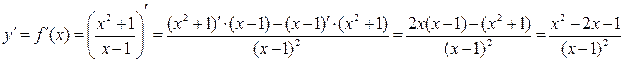 . Производная не существует при
. Производная не существует при 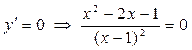 . Дробь обращается в ноль при тех
. Дробь обращается в ноль при тех 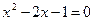 . Решая квадратное уравнение, получаем
. Решая квадратное уравнение, получаем 
 . Поэтому у функции 3 критические точки:
. Поэтому у функции 3 критические точки: 
 . Наносим эти точки на числовую прямую и определяем знаки производной на получившихся интервалах. В нашем примере получились интервалы
. Наносим эти точки на числовую прямую и определяем знаки производной на получившихся интервалах. В нашем примере получились интервалы 
 . Для интервала
. Для интервала  в качестве пробной точки можно взять, например,
в качестве пробной точки можно взять, например,  :
:  . Для интервала
. Для интервала  берем пробную точку
берем пробную точку  :
:  . Для интервала
. Для интервала 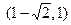 считаем
считаем  . Наконец, для интервала
. Наконец, для интервала 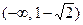 считаем
считаем 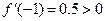 . Расставляем над интервалами полученные знаки производной. Строим итоговую таблицу.
. Расставляем над интервалами полученные знаки производной. Строим итоговую таблицу.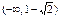
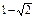



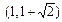


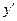


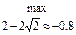
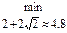
 {после преобразований}
{после преобразований}  ,
,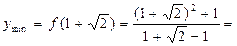 {после преобразований}
{после преобразований}  .
.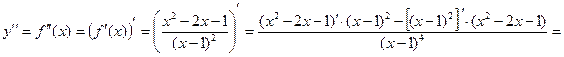
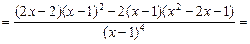

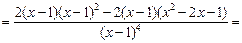
 . Итак,
. Итак,  . Найденная вторая производная существует на всей числовой прямой, кроме все той же точки
. Найденная вторая производная существует на всей числовой прямой, кроме все той же точки  Очевидно, что при
Очевидно, что при 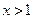 вторая производная
вторая производная  (числитель всегда положителен, знаменатель тоже), а при
(числитель всегда положителен, знаменатель тоже), а при  вторая производная
вторая производная  (числитель всегда положителен, а знаменатель отрицателен). Таким образом, выписываем направления выпуклости графика на интервалах:
(числитель всегда положителен, а знаменатель отрицателен). Таким образом, выписываем направления выпуклости графика на интервалах:  и
и 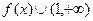 . Точка
. Точка 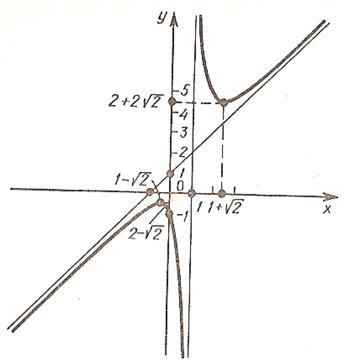
 ,
,  .
.


