
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило Лопиталя вычисления пределовСодержание книги
Поиск на нашем сайте
Мы начинаем изучать приложения понятия производной. Основные приложения (о них мы будем говорить позже) производной Пусть необходимо вычислить предел отношения двух функций
(1)
Если же предел справа в (1) опять дает неопределенность, то правило Лопиталя применяется уже к этому пределу. И так до тех пор, пока неопределенность не исчезнет. Для полноты изложения приведем строгую формулировку теоремы, выражающей правило Лопиталя, хотя для практического его применения в большинстве случаев достаточно запомнить только формулу (1).
1) функции 2) 3) 4) существует (конечный или бесконечный) предел отношения производных Замечание. Правило Лопиталя остается справедливым, если в (1) Интересно, что правило Лопиталя гарантированно работает только в случае возникновения неопределенности. Иначе оно может дать неверный результат. Например, очевидно, что Итак, перед применением правила Лопиталя (1) необходимо проверить наличие неопределенности. Если ее нет, то предел вычисляется обычной подстановкой Пример 1. Пример 2. Пример 3. Пример 4. Пример 5. Пример 6. Однако неопределенности в пределах возникают не только если под знаком предела стоит отношение двух функций, да и список возможных неопределенностей не сводится только к Пример 8. Пример 9.
Неопределенности вида Пример 10. Пример 11.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.247.59 (0.006 с.) |

 функции
функции  состоят в том, что эта производная помогает изучить характер зависимости переменной
состоят в том, что эта производная помогает изучить характер зависимости переменной  от переменной
от переменной  , выраженный видом самой функции
, выраженный видом самой функции 
 , который при подстановке в эту дробь значения
, который при подстановке в эту дробь значения  вместо
вместо  дает неопределенность. Обычно в этом случае возникает неопределенность типа
дает неопределенность. Обычно в этом случае возникает неопределенность типа  или
или  . В этом случае правило Лопиталя говорит о том, что вместо предела отношения исходных функций
. В этом случае правило Лопиталя говорит о том, что вместо предела отношения исходных функций  и
и  можно считать предел отношения их производных
можно считать предел отношения их производных  . Это уже будут другие функции, поэтому предел их отношения возможно неопределенности и не даст, мы сможем его вычислить обычной подстановкой
. Это уже будут другие функции, поэтому предел их отношения возможно неопределенности и не даст, мы сможем его вычислить обычной подстановкой  .
. (за исключением, быть может, самой точки
(за исключением, быть может, самой точки  в указанной окрестности;
в указанной окрестности;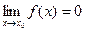 и
и  либо
либо  и
и  (а потому при вычислении
(а потому при вычислении  реально возникает неопределенность
реально возникает неопределенность  );
); .
.  (это и есть формула (1)).
(это и есть формула (1)). или
или  . Справедливо оно и для случая односторонних пределов, если
. Справедливо оно и для случая односторонних пределов, если  или
или  .
. , однако
, однако 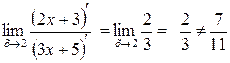 . Поэтому правило Лопиталя (1) для данного примера не работает, поскольку изначально в пределе неопределенности нет, а потому он может быть вычислен простой подстановкой
. Поэтому правило Лопиталя (1) для данного примера не работает, поскольку изначально в пределе неопределенности нет, а потому он может быть вычислен простой подстановкой  (что и было сделано).
(что и было сделано). в выражение под знаком предела. Если же есть, то применяется правило Лопиталя. Рассмотрим примеры.
в выражение под знаком предела. Если же есть, то применяется правило Лопиталя. Рассмотрим примеры. =
= 

 =
= 
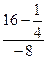 =
= 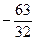 .
. .
.

 ={снова применяем правило Лопиталя}
={снова применяем правило Лопиталя} 
 .
. =
=  =
=  =
=  .
. =
=  =
= 
 .
. =
= 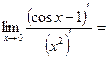
 =
=  = ={вспоминаем первый замечательный предел:
= ={вспоминаем первый замечательный предел:  }
}  .
.

 .
. ,
,  ,
,  ,
,  ,
,  ). Как же раскрывать неопределенность в этих случаях? Поскольку правило Лопиталя (1) применимо только к отношению двух функций с определенным видом неопределенности, то выход один. В этих случаях необходимо так тождественно преобразовать выражение под знаком предела, чтобы оно приняло вид отношения двух функций с неопределенностью
). Как же раскрывать неопределенность в этих случаях? Поскольку правило Лопиталя (1) применимо только к отношению двух функций с определенным видом неопределенности, то выход один. В этих случаях необходимо так тождественно преобразовать выражение под знаком предела, чтобы оно приняло вид отношения двух функций с неопределенностью 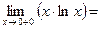 {предел односторонний, так как х, будучи под знаком логарифма, не может принимать отрицательные значения}
{предел односторонний, так как х, будучи под знаком логарифма, не может принимать отрицательные значения}  {для приведения пределу к виду, удобному для применения правила Лопиталя, перенесем х в знаменатель, но, естественно, как
{для приведения пределу к виду, удобному для применения правила Лопиталя, перенесем х в знаменатель, но, естественно, как  }
}  {применяем правило Лопиталя}
{применяем правило Лопиталя}  .
.

 .
.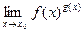 , когда основание и показатель степени стремятся к соответствующим значениям. Свести такой предел к виду, для которого можно применить правило Лопиталя (1), помогает следующий прием. Несложно понять (или вспомнить), что для любых чисел
, когда основание и показатель степени стремятся к соответствующим значениям. Свести такой предел к виду, для которого можно применить правило Лопиталя (1), помогает следующий прием. Несложно понять (или вспомнить), что для любых чисел  и
и  справедливо (из основного логарифмического тождества) представление степени в виде:
справедливо (из основного логарифмического тождества) представление степени в виде: 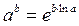 . Поэтому
. Поэтому  . Допустим, что мы выяснили, к чему стремится полученный показатель степени:
. Допустим, что мы выяснили, к чему стремится полученный показатель степени:  . Тогда (из непрерывности функции
. Тогда (из непрерывности функции  ) получим:
) получим:  .
. . Это следует из того, что выше с помощью правила Лопиталя было вычислено
. Это следует из того, что выше с помощью правила Лопиталя было вычислено  .
.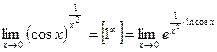 . Остается вычислить предел показателя степени:
. Остается вычислить предел показателя степени: 
 (последний из пределов – первый замечательный предел). Поэтому исходный
(последний из пределов – первый замечательный предел). Поэтому исходный  .
.


