

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Графики основных элементарных функций
 1. Линейная функция. Это функция вида 1. Линейная функция. Это функция вида  , которая уже проходилась ранее в аналитической геометрии (как уравнение прямой с угловым коэффициентом). Число , которая уже проходилась ранее в аналитической геометрии (как уравнение прямой с угловым коэффициентом). Число  называется угловым коэффициентом, а число называется угловым коэффициентом, а число  − свободным членом. Графиком линейной функции служит прямая на координатной плоскости, не параллельная оси − свободным членом. Графиком линейной функции служит прямая на координатной плоскости, не параллельная оси  . Угловой коэффициент . Угловой коэффициент  равен тангенсу угла наклона прямой к положительному направлению оси Ох, а ось у прямая пересекает в точке с координатой равен тангенсу угла наклона прямой к положительному направлению оси Ох, а ось у прямая пересекает в точке с координатой  . .
 2. Квадратичная функция. Это функция вида 2. Квадратичная функция. Это функция вида  . Как известно, графиком квадратичной функции служит парабола с осью, параллельной оси . Как известно, графиком квадратичной функции служит парабола с осью, параллельной оси  . Ветви параболы направлены вверх (если . Ветви параболы направлены вверх (если  ) или вниз (если ) или вниз (если  ). Координаты вершины параболы определяются по формулам: ). Координаты вершины параболы определяются по формулам:  . .
3. Степенная функция. Это функция вида 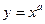 , где , где  − число. Форма графика функции зависит от показателя степени − число. Форма графика функции зависит от показателя степени  . Рассмотрим следующие случаи: . Рассмотрим следующие случаи:
а)  − целое положительное число. Поскольку при любом таком − целое положительное число. Поскольку при любом таком  выполнено выполнено  , то все графики проходят через точки с координатами , то все графики проходят через точки с координатами  и и  . Если число . Если число  − чётное, то функция является чётной (поэтому ее график симметричен относительно оси − чётное, то функция является чётной (поэтому ее график симметричен относительно оси  ). Если число ). Если число  − нечётное, то функция является нечётной (поэтому ее график симметричен относительно начала координат). Иллюстрация − на рисунке. − нечётное, то функция является нечётной (поэтому ее график симметричен относительно начала координат). Иллюстрация − на рисунке.
  б) Если б) Если  есть целое отрицательное число, то функция имеет вид есть целое отрицательное число, то функция имеет вид 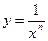 . Ситуация с чётностью и нечётностью при этом такая же, как и для случая целых положительных значений показателя степени . Ситуация с чётностью и нечётностью при этом такая же, как и для случая целых положительных значений показателя степени  . Функция не определена при . Функция не определена при 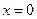 (на 0 делить нельзя), а ее график называют гиперболой (по аналогии со случаем (на 0 делить нельзя), а ее график называют гиперболой (по аналогии со случаем  , когда график действительно является той гиперболой, которая была пройдена раньше). Снова заметим, что , когда график действительно является той гиперболой, которая была пройдена раньше). Снова заметим, что  при всех при всех  . Если . Если  , то , то  при всех при всех  , кроме , кроме  (выражение (выражение  не имеет смысла). Иллюстрация − на рисунке. не имеет смысла). Иллюстрация − на рисунке.
  в). Если в). Если  − дробное положительное число, то, по определению, при − дробное положительное число, то, по определению, при 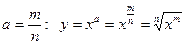 , функция определена при , функция определена при 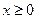 , ,  при всех таких при всех таких  , а графики имеют вид как на рисунке слева. Если , а графики имеют вид как на рисунке слева. Если  − дробное отрицательное число, то, по определению, при − дробное отрицательное число, то, по определению, при  , функция определена при , функция определена при 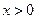 , ,  при всех таких при всех таких  , а графики имеют вид как на рисунке справа. , а графики имеют вид как на рисунке справа.
4. Показательная функция (в частности, экспонента). Это функция вида    . Для неё . Для неё  . Поведение графика зависит от величины основания степени а. При . Поведение графика зависит от величины основания степени а. При  график имеет вид как на рисунке слева, а при график имеет вид как на рисунке слева, а при  как на рисунке справа. как на рисунке справа.
 
При  (известное в математике «число е»: (известное в математике «число е»:  ) показательная функция ) показательная функция  называется экспонентой. называется экспонентой.
5. Логарифмическая функция. Это функция вида  . Функция определена только для . Функция определена только для  , ,  . Поведение графика снова зависит от величины основания логарифма . Поведение графика снова зависит от величины основания логарифма  . На рисунке слева показан вид графика при . На рисунке слева показан вид графика при  , а на рисунке справа при , а на рисунке справа при  . .
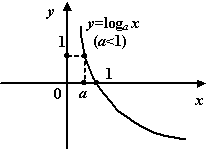 
При наиболее употребляемых основаниях логарифма  и и  получаются так называемые десятичные и натуральные логарифмы с соответствующими принятыми обозначениями: получаются так называемые десятичные и натуральные логарифмы с соответствующими принятыми обозначениями:  и и  . .
6. Тригонометрические функции. К ним относятся функции     . Функция . Функция  нечетна и периодична с периодом нечетна и периодична с периодом  . Её график таков: . Её график таков:

Функция  четна и периодична с периодом четна и периодична с периодом  . Она получается из графика функции . Она получается из графика функции  сдвигом влево на сдвигом влево на  (так как (так как  ). Её график таков: ). Её график таков:

Функция  нечётна и периодична с периодом нечётна и периодична с периодом  . Она не определена в точках . Она не определена в точках  (там, где косинус обращается в 0). Функция (там, где косинус обращается в 0). Функция  нечётна и периодична с периодом нечётна и периодична с периодом  . Она не определена в точках . Она не определена в точках  (там, где синус обращается в 0). Графики функций представлены ниже. (там, где синус обращается в 0). Графики функций представлены ниже.
 
Предел функции
  Высшая математика (условно) отличается от элементарной тем, что в высшей математике вводится понятие предела функции. И все основные понятия высшей математики (непрерывность функции, производная, интеграл, ряды и т.д.) в своих определениях содержат слово «предел». Формальное определение предела функции достаточно абстрактно, а потому сложно для восприятия. Поэтому дадим пока нестрогое, но интуитивно понятное описательное определение предела. Рассмотрим в качестве примера функцию Высшая математика (условно) отличается от элементарной тем, что в высшей математике вводится понятие предела функции. И все основные понятия высшей математики (непрерывность функции, производная, интеграл, ряды и т.д.) в своих определениях содержат слово «предел». Формальное определение предела функции достаточно абстрактно, а потому сложно для восприятия. Поэтому дадим пока нестрогое, но интуитивно понятное описательное определение предела. Рассмотрим в качестве примера функцию 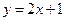 . Будем брать различные числовые значения переменной . Будем брать различные числовые значения переменной  (аргумента функции), приближающиеся (с разных сторон) к числу (аргумента функции), приближающиеся (с разных сторон) к числу 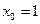 (но не совпадающие с ним), и каждый раз будем вычислять соответствующее значение функции (но не совпадающие с ним), и каждый раз будем вычислять соответствующее значение функции  (см. таблицу). Из таблицы видно, что чем ближе мы подбираемся значениями при (см. таблицу). Из таблицы видно, что чем ближе мы подбираемся значениями при  к числу 1, тем ближе соответствующие значения функции подходят к числу к числу 1, тем ближе соответствующие значения функции подходят к числу 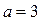 . В этом случае будем говорить, что число 3 является пределом функции . В этом случае будем говорить, что число 3 является пределом функции 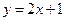 при при  стремящемся к 1. стремящемся к 1.
Перейдем к общему случаю. Пусть функция  определена в окрестности точки (числа) определена в окрестности точки (числа)  за исключением (быть может) самого числа за исключением (быть может) самого числа  . . Число а называется пределом функции  при при  стремящемся к числу стремящемся к числу 
(обозначается:  ), если при безграничном приближении ), если при безграничном приближении  к числу к числу  по любому закону (справа, слева, попеременно и т.д., но по любому закону (справа, слева, попеременно и т.д., но  ), соответствующие значения функции у безгранично приближаются к числу а (одному и тому же при любом законе стремления ), соответствующие значения функции у безгранично приближаются к числу а (одному и тому же при любом законе стремления  к числу к числу  ). Символическая запись того факта, что число а является пределом функции ). Символическая запись того факта, что число а является пределом функции  при при  стремящемся к числу стремящемся к числу  , следующая: , следующая:  . Поэтому для рассмотренной выше функции . Поэтому для рассмотренной выше функции 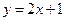 можно записать: можно записать:  . Это «определение» предела, конечно же, математически не строгое, так как не определено, что понимать под «безграничным приближением». Но оно раскрывает суть этого понятия. Строгое определение будет дано ниже на основании понятия предела числовой последовательности и намного более формально. . Это «определение» предела, конечно же, математически не строгое, так как не определено, что понимать под «безграничным приближением». Но оно раскрывает суть этого понятия. Строгое определение будет дано ниже на основании понятия предела числовой последовательности и намного более формально.
Будем далее рассматривать пределы функций не только когда  стремится к определенному числу стремится к определенному числу  , но и когда , но и когда  неограниченно возрастает (будем в этом случае говорить, что неограниченно возрастает (будем в этом случае говорить, что  стремится к плюс бесконечности: стремится к плюс бесконечности:  ) или неограниченно убывает (будем в этом случае говорить, что ) или неограниченно убывает (будем в этом случае говорить, что  стремится к минус бесконечности: стремится к минус бесконечности:  ). Для определения предела функции ). Для определения предела функции  при при  можно, например, «пробежаться» значениями можно, например, «пробежаться» значениями  и проследить, приближаются ли как угодно близко соответствующие значения функции к какому-либо числу. Если это так, то это число будем называть пределом функции и проследить, приближаются ли как угодно близко соответствующие значения функции к какому-либо числу. Если это так, то это число будем называть пределом функции  при при  . Аналогично, при определении предела при . Аналогично, при определении предела при  следует с той же целью «пробежаться», например, значениями следует с той же целью «пробежаться», например, значениями  . .
Пример 1. Найдем с помощью приведенного выше интуитивного определения предела  и и  . Для нахождения первого предела «пройдемся» значениями . Для нахождения первого предела «пройдемся» значениями  . Тогда значениями величины . Тогда значениями величины  будут числа будут числа  .. Таким образом, чем число .. Таким образом, чем число  «ближе к плюс бесконечности», тем значения «ближе к плюс бесконечности», тем значения  ближе к 0. Таким образом, ближе к 0. Таким образом,  . Для нахождения второго предела «пройдемся» значениями . Для нахождения второго предела «пройдемся» значениями  . Тогда значениями величины . Тогда значениями величины  будут числа будут числа  . Поэтому (как и в предыдущем случае), чем число . Поэтому (как и в предыдущем случае), чем число  «ближе к минус бесконечности», тем значения «ближе к минус бесконечности», тем значения  ближе к 0 (только приближение к 0 будет происходить теперь со стороны отрицательных чисел). Таким образом, ближе к 0 (только приближение к 0 будет происходить теперь со стороны отрицательных чисел). Таким образом,  . .
Определим понятие предела числовой последовательности  . Пусть дана бесконечная последовательность чисел . Пусть дана бесконечная последовательность чисел  , занумерованных по порядку: , занумерованных по порядку:  . Эту последовательность можно рассматривать и как множество значений функции . Эту последовательность можно рассматривать и как множество значений функции  (т.е. (т.е. 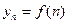 ), определённой на множестве всех натуральных чисел ), определённой на множестве всех натуральных чисел  ., и как просто бесконечный набор чисел, каждое из которых снабжено номером, показывающим место данного числа в этой последовательности. Дадим определение предела последовательности ., и как просто бесконечный набор чисел, каждое из которых снабжено номером, показывающим место данного числа в этой последовательности. Дадим определение предела последовательности  при условии, что номер при условии, что номер 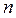 неограниченно растёт (это условие обозначается неограниченно растёт (это условие обозначается  ). Стремление ). Стремление  к бесконечности означает, что при своём изменении номер числа в последовательности становится больше любого наперёд заданного натурального числа к бесконечности означает, что при своём изменении номер числа в последовательности становится больше любого наперёд заданного натурального числа  , то есть, начиная с какого-то члена последовательности (а именно, с , то есть, начиная с какого-то члена последовательности (а именно, с  ), начинает выполняться для номеров членов последовательности неравенство ), начинает выполняться для номеров членов последовательности неравенство  . Если при таком процессе увеличения номера членов последовательности сами эти числа . Если при таком процессе увеличения номера членов последовательности сами эти числа  неограниченно приближаются к некоторому числу неограниченно приближаются к некоторому числу 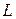 , то это число будем называть пределом этой последовательности, что записывается так: , то это число будем называть пределом этой последовательности, что записывается так:  . .
Формализуем сказанное. Число L называется пределом последовательности  , если для любого, сколь угодно малого, числа , если для любого, сколь угодно малого, числа  (что означает произвольную задаваемую нами степень близости членов последовательности к числу L)можно найти такое число (что означает произвольную задаваемую нами степень близости членов последовательности к числу L)можно найти такое число  (зависящее, конечно, от выбранной нами степени близости (зависящее, конечно, от выбранной нами степени близости 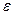 ), что для всех достаточно далеких членов последовательности с номерами ), что для всех достаточно далеких членов последовательности с номерами  будет выполняться неравенство будет выполняться неравенство  (что означает приближение (что означает приближение  к L ближе, чем на к L ближе, чем на 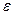 ). С помощью кванторов это определение выглядит компактнее: ). С помощью кванторов это определение выглядит компактнее:  . В этом случае будем также говорить, что последовательность . В этом случае будем также говорить, что последовательность  сходится к числу L и писать: сходится к числу L и писать:  . .
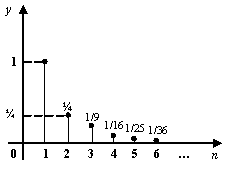 Пример 2. Покажем строго, что предел последовательности Пример 2. Покажем строго, что предел последовательности  равен 0. Рисунок иллюстрирует поведение членов этой последовательности чисел при увеличении их номеров равен 0. Рисунок иллюстрирует поведение членов этой последовательности чисел при увеличении их номеров  . Фиксируем произвольное число . Фиксируем произвольное число  и подберём число и подберём число  в зависимости от в зависимости от 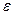 так, чтобы при всех так, чтобы при всех  выполнялось неравенство выполнялось неравенство  , то есть , то есть  . Решая это неравенство относительно . Решая это неравенство относительно  , получаем, что оно выполняется при , получаем, что оно выполняется при  . Значит, достаточно выбрать в качестве . Значит, достаточно выбрать в качестве  натуральное число, не меньшее, чем натуральное число, не меньшее, чем  , и тогда при любом , и тогда при любом  неравенство неравенство  будет выполнено. В качестве такого числа будет выполнено. В качестве такого числа  можно взять, например, ближайшее к можно взять, например, ближайшее к  целое число (что называется его целой частью: целое число (что называется его целой частью: 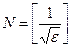 ). По данному выше определению предела числовой последовательности приведенное рассуждение означает, что действительно ). По данному выше определению предела числовой последовательности приведенное рассуждение означает, что действительно  . .
После того, как мы дали строгое определение предела числовой последовательности, можно дать на его основе и строгое определение предела функции. А именно, число а называется пределом функции  при при  стремящемся к числу стремящемся к числу  ( ( ), если для любой числовой последовательности { ), если для любой числовой последовательности {  }, стремящейся к }, стремящейся к  , последовательность соответствующих значений функции , последовательность соответствующих значений функции  стремится к числу а. стремится к числу а.
Для вычисления самого первого предела  нам, используя приведенное выше описательное определение предела, пришлось строить таблицу значений функции нам, используя приведенное выше описательное определение предела, пришлось строить таблицу значений функции  при различных значениях при различных значениях  , приближающихся к 1, и выяснять, к какому числу при этом приближаются значения функции , приближающихся к 1, и выяснять, к какому числу при этом приближаются значения функции  (выяснилось, что к 3). Нельзя ли было каким-либо другим способом получить это значение предела. Можно предложить еще 3 варианта (значительно более строгие, чем предложенное выше построение таблицы). (выяснилось, что к 3). Нельзя ли было каким-либо другим способом получить это значение предела. Можно предложить еще 3 варианта (значительно более строгие, чем предложенное выше построение таблицы).
1. Использовать данное выше строгое математическое определение предела функции. Для данного простого примера это было бы сделать несложно, но для более сложных примеров – практически невозможно.
2. Воспользоваться некоторыми утверждениями, которые дает следующая
Теорема (о пределах). Пусть существуют пределы  и и  , а , а  − некоторое число. Тогда существуют следующие пределы и вычисляются следующим образом. − некоторое число. Тогда существуют следующие пределы и вычисляются следующим образом.
1) вынесение постоянного множителя за знак предела:  . .
2) предел суммы-разности:     = =  . .
3) предел произведения-частного: а)  , б) , б) 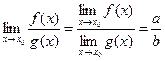 , если , если  . .
4) Если для всех  из некоторой окрестности из некоторой окрестности  (за исключением быть может самого числа (за исключением быть может самого числа  ) выполнено неравенство ) выполнено неравенство  , то и , то и 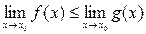 . .
5) Если  − постоянная, то − постоянная, то  . .
6) Замена переменной в пределе: пусть существуют пределы  и и  . Тогда . Тогда   . .
Используя утверждения 1), 2) и 5) этой теоремы, получили бы для нашего примера:  . .
3. Заметим, что если бы мы (желая вычислить  ) сразу бы подставили ) сразу бы подставили  (т.е. то значение, к которому приближается (т.е. то значение, к которому приближается  ) в выражение для функции ) в выражение для функции  (стоящей под знаком предела), то получили бы искомое значение предела: (стоящей под знаком предела), то получили бы искомое значение предела:  .Поэтому в данном случае получилось, что .Поэтому в данном случае получилось, что  . Тогда быть может для любых функций справедливо: . Тогда быть может для любых функций справедливо: 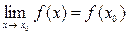 и можно просто подставлять в и можно просто подставлять в  вместо вместо  его предельное значение его предельное значение  ? Это действительно справедливо (и доказывается с использованием приведенной выше теоремы) для многих функций, которые в дальнейшем мы назовем непрерывными в точке ? Это действительно справедливо (и доказывается с использованием приведенной выше теоремы) для многих функций, которые в дальнейшем мы назовем непрерывными в точке  . А пока при решении задач на вычисление пределов можно использовать следующее «мнемоническое» . А пока при решении задач на вычисление пределов можно использовать следующее «мнемоническое»
Правило. Пусть функция  задана в окрестности точки задана в окрестности точки  (за исключением, быть может, самой точки (за исключением, быть может, самой точки  ) единой формулой. Для вычисления предела ) единой формулой. Для вычисления предела  можно попытаться вычислить значение можно попытаться вычислить значение  , т.е. подставить число , т.е. подставить число  вместо вместо  в формулу в формулу  и произвести определяемые формулой вычисления. Если при этом получается «обычное» число а (т.е. не возникают так называемые неопределенности вида и произвести определяемые формулой вычисления. Если при этом получается «обычное» число а (т.е. не возникают так называемые неопределенности вида  и т.п.), то это число и является значением искомого предела: и т.п.), то это число и является значением искомого предела:  . Это правило основано на так называемой непрерывности (это понятие будет пройдено позднее) элементарных функций в своей области определения. . Это правило основано на так называемой непрерывности (это понятие будет пройдено позднее) элементарных функций в своей области определения.
Пример.  . .
Прежде, чем выяснить, как вычислять пределы функций, не подчиняющихся этому правилу (т.е. когда указанные выше неопределенности типа  все же возникают), скажем о так называемых «псевдонеопределенностях», когда при подстановке предельного значения все же возникают), скажем о так называемых «псевдонеопределенностях», когда при подстановке предельного значения  в формулу для в формулу для  тоже получается что-то на первый взгляд необычное, но, как окажется, вполне вычислимое. Ранее, в примере выше было найдено, что тоже получается что-то на первый взгляд необычное, но, как окажется, вполне вычислимое. Ранее, в примере выше было найдено, что  . Это было понятно, поскольку при неограниченном увеличении знаменателя ( . Это было понятно, поскольку при неограниченном увеличении знаменателя ( ), при условии, что числитель при этом стоит на месте (равен 1), дробь неограниченно уменьшается, то есть приближается к 0. Аналогично объясняется и то, что ), при условии, что числитель при этом стоит на месте (равен 1), дробь неограниченно уменьшается, то есть приближается к 0. Аналогично объясняется и то, что  (но теперь приближение к 0 будет происходить со стороны отрицательных чисел, но сути это не меняет). Несложно догадаться, что такой результат будет получаться всегда, если мы вычисляем предел дроби, числитель которой приближается к конкретному конечному числу (или просто равен числу, как в предыдущем примере), а знаменатель неограниченно возрастает или неограниченно убывает (т.е. стремится к (но теперь приближение к 0 будет происходить со стороны отрицательных чисел, но сути это не меняет). Несложно догадаться, что такой результат будет получаться всегда, если мы вычисляем предел дроби, числитель которой приближается к конкретному конечному числу (или просто равен числу, как в предыдущем примере), а знаменатель неограниченно возрастает или неограниченно убывает (т.е. стремится к  или к или к  ). Поэтому можно сформулировать ). Поэтому можно сформулировать
Первое правило для псевдонеопределенности: если при вычислении предела от дроби получается (при подстановке в нее вместо  его предельного значения) выражение типа его предельного значения) выражение типа  , то предел равен 0. , то предел равен 0.
Теперь попробуем вычислить  . Если мы начнем приближаться по . Если мы начнем приближаться по  к нулю со стороны положительных чисел (беря, например, к нулю со стороны положительных чисел (беря, например,  ), то значения функции ), то значения функции  ( ( ) стремятся к ) стремятся к  . Однако, если мы пойдем к 0 со стороны отрицательных чисел ( . Однако, если мы пойдем к 0 со стороны отрицательных чисел ( ), то значения этой функции ( ), то значения этой функции ( ) стремятся уже к ) стремятся уже к  . Поэтому в обычном смысле . Поэтому в обычном смысле  не существует, так как по определению предела к предельному значению (одному и тому же!) значения функции должны безгранично приближаться при любом законе приближения не существует, так как по определению предела к предельному значению (одному и тому же!) значения функции должны безгранично приближаться при любом законе приближения  к своему предельному значению. Однако в этом случае существуют так называемые односторонние пределы, о которых речь пойдет позже. Чисто символически описанный выше факт можно записать в форме: к своему предельному значению. Однако в этом случае существуют так называемые односторонние пределы, о которых речь пойдет позже. Чисто символически описанный выше факт можно записать в форме:  . Обобщив этот пример, получим . Обобщив этот пример, получим
Второе правило для псевдонеопределенности: если при вычислении предела от дроби получается (при подстановке в нее вместо  его предельного значения) выражение типа его предельного значения) выражение типа  , то предел равен , то предел равен  . .
|


 при
при  стремящемся к числу
стремящемся к числу 
 ), если при безграничном приближении
), если при безграничном приближении  к числу
к числу  по любому закону (справа, слева, попеременно и т.д., но
по любому закону (справа, слева, попеременно и т.д., но  ), соответствующие значения функции у безгранично приближаются к числу а (одному и тому же при любом законе стремления
), соответствующие значения функции у безгранично приближаются к числу а (одному и тому же при любом законе стремления  к числу
к числу  ). Символическая запись того факта, что число а является пределом функции
). Символическая запись того факта, что число а является пределом функции  при
при  стремящемся к числу
стремящемся к числу  , следующая:
, следующая:  . Поэтому для рассмотренной выше функции
. Поэтому для рассмотренной выше функции 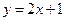 можно записать:
можно записать:  . Это «определение» предела, конечно же, математически не строгое, так как не определено, что понимать под «безграничным приближением». Но оно раскрывает суть этого понятия. Строгое определение будет дано ниже на основании понятия предела числовой последовательности и намного более формально.
. Это «определение» предела, конечно же, математически не строгое, так как не определено, что понимать под «безграничным приближением». Но оно раскрывает суть этого понятия. Строгое определение будет дано ниже на основании понятия предела числовой последовательности и намного более формально.
 1. Линейная функция. Это функция вида
1. Линейная функция. Это функция вида  , которая уже проходилась ранее в аналитической геометрии (как уравнение прямой с угловым коэффициентом). Число
, которая уже проходилась ранее в аналитической геометрии (как уравнение прямой с угловым коэффициентом). Число  называется угловым коэффициентом, а число
называется угловым коэффициентом, а число  − свободным членом. Графиком линейной функции служит прямая на координатной плоскости, не параллельная оси
− свободным членом. Графиком линейной функции служит прямая на координатной плоскости, не параллельная оси  . Угловой коэффициент
. Угловой коэффициент  2. Квадратичная функция. Это функция вида
2. Квадратичная функция. Это функция вида  . Как известно, графиком квадратичной функции служит парабола с осью, параллельной оси
. Как известно, графиком квадратичной функции служит парабола с осью, параллельной оси  ) или вниз (если
) или вниз (если  ). Координаты вершины параболы определяются по формулам:
). Координаты вершины параболы определяются по формулам:  .
.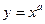 , где
, где  − число. Форма графика функции зависит от показателя степени
− число. Форма графика функции зависит от показателя степени  − целое положительное число. Поскольку при любом таком
− целое положительное число. Поскольку при любом таком  , то все графики проходят через точки с координатами
, то все графики проходят через точки с координатами  и
и  ). Если число
). Если число 
 б) Если
б) Если  есть целое отрицательное число, то функция имеет вид
есть целое отрицательное число, то функция имеет вид 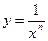 . Ситуация с чётностью и нечётностью при этом такая же, как и для случая целых положительных значений показателя степени
. Ситуация с чётностью и нечётностью при этом такая же, как и для случая целых положительных значений показателя степени 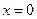 (на 0 делить нельзя), а ее график называют гиперболой (по аналогии со случаем
(на 0 делить нельзя), а ее график называют гиперболой (по аналогии со случаем  , когда график действительно является той гиперболой, которая была пройдена раньше). Снова заметим, что
, когда график действительно является той гиперболой, которая была пройдена раньше). Снова заметим, что  при всех
при всех  , то
, то  при всех
при всех  (выражение
(выражение  не имеет смысла). Иллюстрация − на рисунке.
не имеет смысла). Иллюстрация − на рисунке.
 в). Если
в). Если 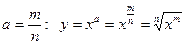 , функция определена при
, функция определена при 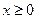 ,
,  при всех таких
при всех таких  , функция определена при
, функция определена при 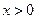 ,
, 

 . Для неё
. Для неё  . Поведение графика зависит от величины основания степени а. При
. Поведение графика зависит от величины основания степени а. При  график имеет вид как на рисунке слева, а при
график имеет вид как на рисунке слева, а при  как на рисунке справа.
как на рисунке справа.

 (известное в математике «число е»:
(известное в математике «число е»:  ) показательная функция
) показательная функция  называется экспонентой.
называется экспонентой. . Функция определена только для
. Функция определена только для  ,
,  . Поведение графика снова зависит от величины основания логарифма
. Поведение графика снова зависит от величины основания логарифма  , а на рисунке справа при
, а на рисунке справа при  .
.

 и
и  получаются так называемые десятичные и натуральные логарифмы с соответствующими принятыми обозначениями:
получаются так называемые десятичные и натуральные логарифмы с соответствующими принятыми обозначениями:  и
и  .
.


 . Функция
. Функция  нечетна и периодична с периодом
нечетна и периодична с периодом  . Её график таков:
. Её график таков:
 четна и периодична с периодом
четна и периодична с периодом  сдвигом влево на
сдвигом влево на  (так как
(так как  ). Её график таков:
). Её график таков:
 нечётна и периодична с периодом
нечётна и периодична с периодом  . Она не определена в точках
. Она не определена в точках  (там, где косинус обращается в 0). Функция
(там, где косинус обращается в 0). Функция  нечётна и периодична с периодом
нечётна и периодична с периодом  (там, где синус обращается в 0). Графики функций представлены ниже.
(там, где синус обращается в 0). Графики функций представлены ниже.


 Высшая математика (условно) отличается от элементарной тем, что в высшей математике вводится понятие предела функции. И все основные понятия высшей математики (непрерывность функции, производная, интеграл, ряды и т.д.) в своих определениях содержат слово «предел». Формальное определение предела функции достаточно абстрактно, а потому сложно для восприятия. Поэтому дадим пока нестрогое, но интуитивно понятное описательное определение предела. Рассмотрим в качестве примера функцию
Высшая математика (условно) отличается от элементарной тем, что в высшей математике вводится понятие предела функции. И все основные понятия высшей математики (непрерывность функции, производная, интеграл, ряды и т.д.) в своих определениях содержат слово «предел». Формальное определение предела функции достаточно абстрактно, а потому сложно для восприятия. Поэтому дадим пока нестрогое, но интуитивно понятное описательное определение предела. Рассмотрим в качестве примера функцию 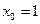 (но не совпадающие с ним), и каждый раз будем вычислять соответствующее значение функции
(но не совпадающие с ним), и каждый раз будем вычислять соответствующее значение функции  (см. таблицу). Из таблицы видно, что чем ближе мы подбираемся значениями при
(см. таблицу). Из таблицы видно, что чем ближе мы подбираемся значениями при  к числу 1, тем ближе соответствующие значения функции подходят к числу
к числу 1, тем ближе соответствующие значения функции подходят к числу 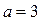 . В этом случае будем говорить, что число 3 является пределом функции
. В этом случае будем говорить, что число 3 является пределом функции  ) или неограниченно убывает (будем в этом случае говорить, что
) или неограниченно убывает (будем в этом случае говорить, что  ). Для определения предела функции
). Для определения предела функции  и проследить, приближаются ли как угодно близко соответствующие значения функции к какому-либо числу. Если это так, то это число будем называть пределом функции
и проследить, приближаются ли как угодно близко соответствующие значения функции к какому-либо числу. Если это так, то это число будем называть пределом функции  .
. и
и  . Для нахождения первого предела «пройдемся» значениями
. Для нахождения первого предела «пройдемся» значениями  будут числа
будут числа  .. Таким образом, чем число
.. Таким образом, чем число  ближе к 0. Таким образом,
ближе к 0. Таким образом,  . Для нахождения второго предела «пройдемся» значениями
. Для нахождения второго предела «пройдемся» значениями  . Поэтому (как и в предыдущем случае), чем число
. Поэтому (как и в предыдущем случае), чем число  .
. . Пусть дана бесконечная последовательность чисел
. Пусть дана бесконечная последовательность чисел  . Эту последовательность можно рассматривать и как множество значений функции
. Эту последовательность можно рассматривать и как множество значений функции  (т.е.
(т.е. 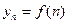 ), определённой на множестве всех натуральных чисел
), определённой на множестве всех натуральных чисел  ., и как просто бесконечный набор чисел, каждое из которых снабжено номером, показывающим место данного числа в этой последовательности. Дадим определение предела последовательности
., и как просто бесконечный набор чисел, каждое из которых снабжено номером, показывающим место данного числа в этой последовательности. Дадим определение предела последовательности 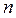 неограниченно растёт (это условие обозначается
неограниченно растёт (это условие обозначается  ). Стремление
). Стремление  к бесконечности означает, что при своём изменении номер числа в последовательности становится больше любого наперёд заданного натурального числа
к бесконечности означает, что при своём изменении номер числа в последовательности становится больше любого наперёд заданного натурального числа  , то есть, начиная с какого-то члена последовательности (а именно, с
, то есть, начиная с какого-то члена последовательности (а именно, с  ), начинает выполняться для номеров членов последовательности неравенство
), начинает выполняться для номеров членов последовательности неравенство  . Если при таком процессе увеличения номера членов последовательности сами эти числа
. Если при таком процессе увеличения номера членов последовательности сами эти числа  неограниченно приближаются к некоторому числу
неограниченно приближаются к некоторому числу 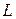 , то это число будем называть пределом этой последовательности, что записывается так:
, то это число будем называть пределом этой последовательности, что записывается так:  .
. , если для любого, сколь угодно малого, числа
, если для любого, сколь угодно малого, числа  (что означает произвольную задаваемую нами степень близости членов последовательности к числу L)можно найти такое число
(что означает произвольную задаваемую нами степень близости членов последовательности к числу L)можно найти такое число  (зависящее, конечно, от выбранной нами степени близости
(зависящее, конечно, от выбранной нами степени близости 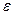 ), что для всех достаточно далеких членов последовательности с номерами
), что для всех достаточно далеких членов последовательности с номерами  будет выполняться неравенство
будет выполняться неравенство  (что означает приближение
(что означает приближение  к L ближе, чем на
к L ближе, чем на  . В этом случае будем также говорить, что последовательность
. В этом случае будем также говорить, что последовательность  .
. Пример 2. Покажем строго, что предел последовательности
Пример 2. Покажем строго, что предел последовательности  равен 0. Рисунок иллюстрирует поведение членов этой последовательности чисел при увеличении их номеров
равен 0. Рисунок иллюстрирует поведение членов этой последовательности чисел при увеличении их номеров  . Фиксируем произвольное число
. Фиксируем произвольное число  , то есть
, то есть  . Решая это неравенство относительно
. Решая это неравенство относительно  . Значит, достаточно выбрать в качестве
. Значит, достаточно выбрать в качестве  , и тогда при любом
, и тогда при любом 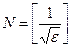 ). По данному выше определению предела числовой последовательности приведенное рассуждение означает, что действительно
). По данному выше определению предела числовой последовательности приведенное рассуждение означает, что действительно  .
. }, стремящейся к
}, стремящейся к  стремится к числу а.
стремится к числу а. нам, используя приведенное выше описательное определение предела, пришлось строить таблицу значений функции
нам, используя приведенное выше описательное определение предела, пришлось строить таблицу значений функции  при различных значениях
при различных значениях  и
и  , а
, а  .
.


 =
=  .
. , б)
, б) 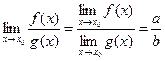 , если
, если  .
. , то и
, то и 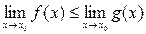 .
. − постоянная, то
− постоянная, то  .
. и
и  . Тогда
. Тогда 
 .
. ) сразу бы подставили
) сразу бы подставили  (т.е. то значение, к которому приближается
(т.е. то значение, к которому приближается  (стоящей под знаком предела), то получили бы искомое значение предела:
(стоящей под знаком предела), то получили бы искомое значение предела:  .Поэтому в данном случае получилось, что
.Поэтому в данном случае получилось, что  . Тогда быть может для любых функций справедливо:
. Тогда быть может для любых функций справедливо: 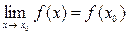 и можно просто подставлять в
и можно просто подставлять в  вместо
вместо  задана в окрестности точки
задана в окрестности точки  можно попытаться вычислить значение
можно попытаться вычислить значение  , т.е. подставить число
, т.е. подставить число  и т.п.), то это число и является значением искомого предела:
и т.п.), то это число и является значением искомого предела:  . Это правило основано на так называемой непрерывности (это понятие будет пройдено позднее) элементарных функций в своей области определения.
. Это правило основано на так называемой непрерывности (это понятие будет пройдено позднее) элементарных функций в своей области определения. .
. . Это было понятно, поскольку при неограниченном увеличении знаменателя (
. Это было понятно, поскольку при неограниченном увеличении знаменателя ( (но теперь приближение к 0 будет происходить со стороны отрицательных чисел, но сути это не меняет). Несложно догадаться, что такой результат будет получаться всегда, если мы вычисляем предел дроби, числитель которой приближается к конкретному конечному числу (или просто равен числу, как в предыдущем примере), а знаменатель неограниченно возрастает или неограниченно убывает (т.е. стремится к
(но теперь приближение к 0 будет происходить со стороны отрицательных чисел, но сути это не меняет). Несложно догадаться, что такой результат будет получаться всегда, если мы вычисляем предел дроби, числитель которой приближается к конкретному конечному числу (или просто равен числу, как в предыдущем примере), а знаменатель неограниченно возрастает или неограниченно убывает (т.е. стремится к  или к
или к  ). Поэтому можно сформулировать
). Поэтому можно сформулировать , то предел равен 0.
, то предел равен 0. . Если мы начнем приближаться по
. Если мы начнем приближаться по  ), то значения функции
), то значения функции  (
( ) стремятся к
) стремятся к  . Однако, если мы пойдем к 0 со стороны отрицательных чисел (
. Однако, если мы пойдем к 0 со стороны отрицательных чисел ( ), то значения этой функции (
), то значения этой функции ( ) стремятся уже к
) стремятся уже к  не существует, так как по определению предела к предельному значению (одному и тому же!) значения функции должны безгранично приближаться при любом законе приближения
не существует, так как по определению предела к предельному значению (одному и тому же!) значения функции должны безгранично приближаться при любом законе приближения  . Обобщив этот пример, получим
. Обобщив этот пример, получим , то предел равен
, то предел равен  .
.


