
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел V. Дифференциальное исчисление функции одного переменногоСодержание книги
Поиск на нашем сайте
Производная функции
Если бы это отношение оказалось (по модулю) больше 1, то мы бы могли сказать, что функция изменилась больше (или быстрее) по отношению к изменению аргумента от (1) Пример 1. Найти производную Решение. Найдем выражение для приращения функции Пример 2. Теперь попробуем найти производную функции Отметим одно важное соотношение, связанное с производной. Из определения производной (1) следует, что при приближении приращения аргумента (2) Функция
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.153 (0.005 с.) |

 Понятие производной функции является одним из фундаментальных понятий высшей математики. Она (производная) дает количественную оценку скорости изменения функции в каждой точке. Введем сначала понятия приращения аргумента в данной точке и соответствующего приращения функции. Пусть функция
Понятие производной функции является одним из фундаментальных понятий высшей математики. Она (производная) дает количественную оценку скорости изменения функции в каждой точке. Введем сначала понятия приращения аргумента в данной точке и соответствующего приращения функции. Пусть функция 
 задана в окрестности некоторой точки
задана в окрестности некоторой точки  на оси Ох. Вычислим значение функции в этой точке
на оси Ох. Вычислим значение функции в этой точке  . Теперь сдвинемся от точки
. Теперь сдвинемся от точки  (вправо, если число
(вправо, если число  , или влево, если
, или влево, если  ). Мы попадем уже в другую точку на оси Ох, которая соответствует числу
). Мы попадем уже в другую точку на оси Ох, которая соответствует числу 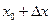 . Снова вычислим значение функции в получившейся точке:
. Снова вычислим значение функции в получившейся точке:  . Определим величину изменения функции
. Определим величину изменения функции  , которая соответствует величине
, которая соответствует величине  в точке
в точке  .
. . Если мы будем теперь неограниченно уменьшать
. Если мы будем теперь неограниченно уменьшать  к приращению аргумента
к приращению аргумента  . Последние два обозначения связаны с понятием дифференциала функции, о котором пойдет речь позже, поэтому пока будем использовать первые два. Итак, по определению производной ее значение в произвольной точке
. Последние два обозначения связаны с понятием дифференциала функции, о котором пойдет речь позже, поэтому пока будем использовать первые два. Итак, по определению производной ее значение в произвольной точке 
 в точке 2. В этом случае
в точке 2. В этом случае  ,
,  .
. .
.  По смыслу производной можно сказать, что в точке 2 функция
По смыслу производной можно сказать, что в точке 2 функция  . Тогда по определению производной
. Тогда по определению производной  Итак,
Итак,  Поскольку точка
Поскольку точка 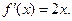 . Это записывается в виде
. Это записывается в виде  . При
. При  получаем значение производной, равное 4, что и было получено в предыдущем примере.
получаем значение производной, равное 4, что и было получено в предыдущем примере. приближается к числу
приближается к числу  . Таким образом, при малых значениях
. Таким образом, при малых значениях 
 .
. ). Функция
). Функция  , если она дифференцируема в каждой точке этого интервала.
, если она дифференцируема в каждой точке этого интервала.


