
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольшее и наименьшее значение функции, непрерывной на отрезкеСодержание книги
Поиск на нашем сайте
Выше, при изучении свойств функций, непрерывных на отрезке, мы уже отмечали, что такие функции достигают (в каких-либо точках) своего наибольшего и наименьшего значения. Теперь уже можно дать конкретный алгоритм отыскания таких значений. Пусть задана непрерывная на отрезке
На рисунке а) наименьшее значение достигается во внутренней точке отрезка (которая является точкой минимума этой функции на интервале Алгоритм поиска наибольшего и наименьшего значения функции 1. Находим критические точки функции, принадлежащие интервалу 2. Вычисляем значения функции на концах интервала и в полученных критических точках: 3. Выбрать из полученных чисел наибольшее и наименьшее.
Пример 1. Найти наибольшее и наименьшее значение функции В этом примере 1. Находим 2. Вычисляем значения исследуемой функции на концах интервала и в найденной критической точке: 3. Выбираем из этих чисел наименьшее и наибольшее: Ответ. Наименьшее значение Многие задачи на поиск наименьшего и наибольшего значения функции возникают на практике как задачи на поиск оптимального решения проблемы.
Попробуем обобщить задачу. А если бы отсутствовало требование прямоугольности участка? Допустим, можно строить участок любой формы, лишь бы он огораживался данным забором длиной 120 метров. Таким образом, приходим к следующей задаче: найти замкнутую кривую длиной 120 метров, которая бы ограничивала фигуру наибольшей площади. Будет ли это опять квадрат со стороной 30 м и площадью 900 м2 ? Это сложная задача, ее нельзя решить теми математическими методами, которые мы уже прошли. Убедимся хотя бы в том, что квадрат, будучи по площади оптимальной фигурой среди всех прямоугольников с заданным периметром, уже не будет оптимальным среди фигур произвольной формы с заданным периметром. Посмотрим, какой бы площади оказался, например, участок круговой формы, ограниченный все тем же забором (см. рисунок). Найдем радиус
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.153 (0.006 с.) |

 функция
функция  , а M и m ее набольшее и наименьшее на этом отрезке значения, которых она обязана достигать. В каких же точках могут достигаться эти значения? На рисунках приведены некоторые возможные варианты.
, а M и m ее набольшее и наименьшее на этом отрезке значения, которых она обязана достигать. В каких же точках могут достигаться эти значения? На рисунках приведены некоторые возможные варианты.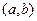 ), а наибольшее − на его правом конце. На рисунке б) наименьшее значение снова достигается внутри отрезка, а наибольшее − на обоих концах отрезка. Наконец, на рисунке в) наименьшее значение принимается на левом конце отрезка, а наибольшее − во внутренней точке
), а наибольшее − на его правом конце. На рисунке б) наименьшее значение снова достигается внутри отрезка, а наибольшее − на обоих концах отрезка. Наконец, на рисунке в) наименьшее значение принимается на левом конце отрезка, а наибольшее − во внутренней точке  . Таким образом, наибольшее и наименьшее значения могут достигаться либо во внутренних точках отрезка (т.е. в точках интервала
. Таким образом, наибольшее и наименьшее значения могут достигаться либо во внутренних точках отрезка (т.е. в точках интервала  (их может и не быть, если функция на этом интервале монотонна − только возрастает или только убывает).
(их может и не быть, если функция на этом интервале монотонна − только возрастает или только убывает).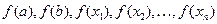 .
. на отрезке
на отрезке 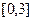 .
. ,
,  ,
, 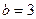 . Идем по пунктам сформулированного алгоритма.
. Идем по пунктам сформулированного алгоритма. . Производная снова существует везде, поэтому критические точки совпадают со стационарными:
. Производная снова существует везде, поэтому критические точки совпадают со стационарными: 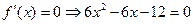 . Решая квадратное, получаем критические точки
. Решая квадратное, получаем критические точки  ,
,  . Однако только
. Однако только  .
.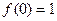 ,
,  ,
,  .
. ,
,  .
. , наибольшее
, наибольшее 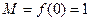 .
. Обозначим размеры участка
Обозначим размеры участка  и
и  (см. рисунок). Нужно выбрать эти размеры так, чтобы площадь была наибольшей. Площадь прямоугольника
(см. рисунок). Нужно выбрать эти размеры так, чтобы площадь была наибольшей. Площадь прямоугольника  . Но мы не умеем (пока) искать максимальное значение функции двух переменных
. Но мы не умеем (пока) искать максимальное значение функции двух переменных  . Выразим отсюда
. Выразим отсюда  , и подставим в формулу для площади. Получим теперь формулу площади
, и подставим в формулу для площади. Получим теперь формулу площади 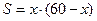 . Ясно, что одна сторона забора может меняться в пределах от 0 до 60. Поэтому мы пришли к следующей математической постановке задачи: Найти наибольшее значение функции
. Ясно, что одна сторона забора может меняться в пределах от 0 до 60. Поэтому мы пришли к следующей математической постановке задачи: Найти наибольшее значение функции  на отрезке
на отрезке  . Используем приведенный выше алгоритм. Производная
. Используем приведенный выше алгоритм. Производная  − единственная критическая точка. Считаем значения функции на концах интервала и в критической точке:
− единственная критическая точка. Считаем значения функции на концах интервала и в критической точке:  (смысл этих нулей понятен),
(смысл этих нулей понятен),  . Наибольшее значение
. Наибольшее значение  , достигается при
, достигается при  . При этом вторая переменная
. При этом вторая переменная  . Итак, наибольшую площадь 900 м2 из всех прямоугольных участков имеет квадратный участок размером 30 на 30 метров. Такого размера прямоугольный участок и надо огораживать, если иметь целью сделать его площадь максимальной.
. Итак, наибольшую площадь 900 м2 из всех прямоугольных участков имеет квадратный участок размером 30 на 30 метров. Такого размера прямоугольный участок и надо огораживать, если иметь целью сделать его площадь максимальной. такого круга. Поскольку длина граничной окружности должна быть 120 метров, то, используя формулу длины окружности, получаем
такого круга. Поскольку длина граничной окружности должна быть 120 метров, то, используя формулу длины окружности, получаем  , откуда
, откуда  . Найдем площадь такого кругового участка:
. Найдем площадь такого кругового участка:  м2. Уже больше площади
м2. Уже больше площади  м2 найденного выше квадрата. Поэтому, если бы не оговаривалась прямоугольная форма участка, то выгоднее строить участок круговой формы. Можно (но сложно) доказать, что круг оптимален среди фигур любой формы с заданным периметром.
м2 найденного выше квадрата. Поэтому, если бы не оговаривалась прямоугольная форма участка, то выгоднее строить участок круговой формы. Можно (но сложно) доказать, что круг оптимален среди фигур любой формы с заданным периметром.



